Prim算法实现最小生成树-Toy模板网

这篇具有很好参考价值的文章主要介绍了Prim算法实现最小生成树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.最小生成树是什么

对连通图进行遍历,过程中所经过的边和顶点的组合可看做是一棵普通树,通常称为生成树。
如果连通图G的一个子图是一棵包含G的所有顶点的树，则该子图称为G的生成树(SpanningTree)。
生成树是连通图的包含图中的所有顶点的极小连通子图。
图的生成树不惟一。从不同的顶点出发进行遍历，可以得到不同的生成树。
最小生成树（minimum spanning tree）其实就是一个生成树，不过它不同于一般的生成树，它的边权之和是最小的，即边权和最小的生成树。
同一个图的最小生成树也可以有很多个，但是其边权和肯定是一样的。

2.最小生成树的用途

最小生成树应用于图论知识的实际问题。生成树和最小生成树有许多重要的应用。

例如：要在n个城市之间铺设光缆，主要目标是要使这n个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

3.Prim算法描述

将图中所有顶点分为两类：树顶点（已被选入生成树的顶点）和非树顶点（还未被选入生成树的顶点）。首先选择任意一个顶点加入生成树，接下来找出一条边添加到生成树，这需要枚举每一个树顶点到每一个非树顶点所有的边，然后找到最短的边加入到生成树中。一直重复直至所有顶点都加入生成树中。
算法的具体流程如下：

从任意一个顶点（假设选1）开始构造生成树，首先将顶点1加入生成树中，用一个一维数组book标记那些顶点已经加入到了生成树中。
用数组dis记录生成树到各个顶点的距离。最初生成树只有1号顶点，有直连边时，数组dis中存储的就是1号顶点到该顶点的边的权值，没有直连边的时候就是无穷大(INT_MAX)，即初始化数组。
从数组dis中选出离生成树最近的顶点（假设为顶点j）加入到生成树中（在数组dis中的最小值）。再以j为中间点，更新生成树到每一个非树顶点的距离，如果dis[k] > e[j][k]则更新dis[k] = e[j][k]。
重复步骤3，直到生成树中有n个顶点为止。

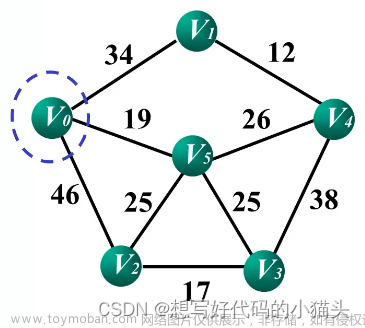
4.Prim算法演示最小生成树过程

图的数据结构描述：
如下图所示，用一个二维矩阵graph表示边的顶点和边信息，例如graph[1][2] = 11表示顶点1到顶点2的权重是11.
一维数组book表示节点i是否被访问过，book[i] = 1表示节点i已经被访问，否则表示还没有被访问。
一维数组dis表示生成树到各个顶点的距离。

Prim算法实现最小生成树

初始化与图相关的所有数据结构，如下所示：

Prim算法实现最小生成树

Prim算法实现的具体步骤如下：

Prim算法实现最小生成树

5.Prim算法实现

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

/*
* 测试用例
2 4 11
3 5 13
4 6 3
5 6 4
2 3 6
4 5 7
1 2 1
3 4 9
1 3 2
*/
class Prim
{
private:
    int vertice = 0;//顶点数
    int edge = 0;//边数
    vector<bool> book;//记录顶点i是否被遍历过
    vector<int> dis;//记录最短距离
    vector<vector<int>> graph;
    int sum = 0;//记录最小生成树权值总和
    int count = 0;//记录最小生成树中节点个数
    int index = 0;//记录dis中最小值的顶点

public:
    Prim(int x = 0, int y = 0) :vertice(x), edge(y)
    {
        graph.resize(vertice + 1);
        for (int i = 0;i <= vertice; i++)
        {
            graph[i].resize(vertice + 1,INT_MAX);
        }
        book.resize(vertice + 1, 0);
        dis.resize(vertice + 1, INT_MAX);
    }

    //图以及图相关的数据结构初始化
    void Init_Graph()
    {
        int u = 0, v = 0, w = 0;
        for (int i = 0; i < edge; i++)
        {
            cin >> u >> v >> w;
            graph[u][v] = w;
            graph[v][u] = w;//无向图的初始化
        }
        for (int i = 1; i <= vertice; i++)
        {
            if (graph[1][i] != INT_MAX)
            {
                dis[i] = graph[1][i];
            }
        }
        book[1] = true;
        cout << "1 -->";
        count++;
    }

    int Prim_Alg()
    {        
        while (count < vertice)
        {
            int min = INT_MAX;
            //找dis中的最小值
            for (int i = 1; i <= vertice; i++)
            {
                if (book[i] == false && dis[i] < min)
                {
                    min = dis[i];
                    index = i;
                }
            }
            cout << index << "-->";
            book[index] = true;
            count++;
            sum += dis[index];

            //扫描以index为到达的所有边，更新dis数组
            for (int i = 1; i <= vertice; i++)
            {
                if (book[i] == false && dis[i] > graph[index][i])
                {
                    dis[i] = graph[index][i];
                }
            }
        }
        return sum;
    }
};

int main()
{
    Prim prim(6,9); 

    cout << "请输入边的信息：" << endl;
    prim.Init_Graph();

    int sum = prim.Prim_Alg();
    cout << "NULL"<<endl<<"最小生成树权重："<<sum << endl;
    return 0;
}