1.2 密码学及安全技术

1.2.1 密码学知识
1.2.1.1 Hash函数
-
Hash(哈希)
哈希函数是一类数学函数,可以在有限合理的时间内,将任意长度的消息压缩为
固定长度的输出值,并且是不可逆的。其输出值称为哈希值,也称为散列值。
-
哈希算法的应用:
消息认证:确保收到的消息和发送的消息都是未被篡改的。
数字签名:对消息摘要进行数字签名与对消息本身进行数字签名等效。
口令的安全性:仅将口令的哈希值进行保存,进行口令检验时仅需对比哈希值即可,即使攻击者获取了口令的哈希值,也无法计算出口令。
数据完整性:具有抗数据篡改的能力。 -
Hash函数在区块链中的应用

在区块链系统中,哈希算法得到了广泛的使用。
在区块链系统中,区块之间的链接就是通过区块的哈希值串联起来的。除此以外,还有梅克尔树的生成计算,交易事务的哈希值计算等。
区块链是一个使用哈希指针构建的链表 -
Merkle tree
Merkle(默克尔)树,又叫哈希树,是一种典型的二叉树结构,由一个根节点、一组中间节点和一组叶节点组成
应用场景:
快速比较大量数据
快速定位修改
1.2.1.2椭圆曲线加密算法
即:Elliptic Curve Cryptography,简称ECC,是基于椭圆曲线数学理论实现的一种非对称加密算法。 相比RSA,ECC优势是可以使用更短的密钥,来实现与RSA相当或更高的安全。据研究,160位ECC加密安全性相当于1024位RSA加密,210位ECC加密安全性相当于2048位RSA加密。
1.2.2 安全技术
1.2.2.1 数字签名
用于防止消息篡改和抵赖的场景
数字签名基于非对称加密,既可以用于证实内容的完整性,又同时可以确 认来源(或不可抵赖,Non-Repudiation)。
数字签名的全过程分两大部分,即签名与验证。一侧为签名,一侧为验证 过程。
1.2.2.2 数字证书

1.2.2.3 PKI体系

1.2.2.4 同态加密
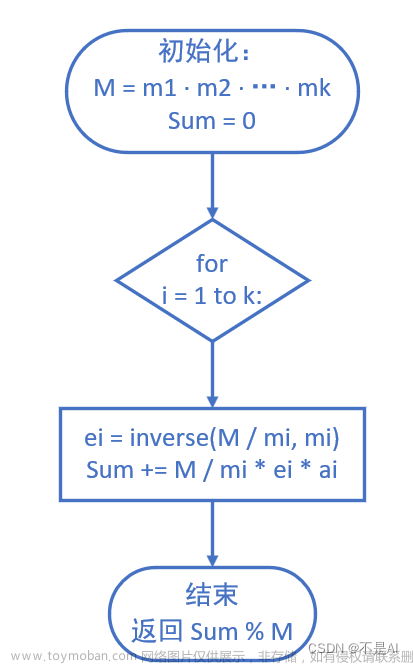
本质上,同态加密是指这样一种加密函数,对明文进行环上的加法和乘法运算再加密,与加密后对密文进行相应的运算,结果是等价的。由于这个良好的性质,人们可以委托第三方对数据进行处理而不泄露信息。具有同态性质的加密函数是指两个明文a、b满足Dec(En(a)⊙En(b))=a⊕b的加密函数,其中En是加密运算,Dec是解密运算,⊙、⊕分别对应明文和密文域上的运算。当⊕代表加法时,称该加密为加同态加密:当⊕代表乘法时,称该加密为乘同态加密。文章来源:https://www.toymoban.com/news/detail-503020.html
全同态加密是指同时满足加同态和乘同态性质,可以进行任意多次加和乘运算的加密函数。用数学公式来表达,即Dec(f(En(m1),En(m2),…,En(mk)))=f(m1,m2,…,mk),或写成:f(En(m1),En(m2),…,En(mk))=En(f(m1,m2,…,mk)),如果f是任意函数,称为全同态加密。文章来源地址https://www.toymoban.com/news/detail-503020.html
1.2.2.5 布隆过滤器
class BloomHash {
/**
* Hash工具类返回的hashcode的最大长度<br>
* maxLength为2的n次方,返回的hashcode为[0,2^n-1]
*/
public int maxLength;
// Hash函数生成哈希码的关键字
public int seed;
public BloomHash(int maxLength, int seed) {
this.maxLength = maxLength;
this.seed = seed;
}
/**
* 返回字符串string的hashcode,大小为[0,maxLength-1]
*
* @param string
* @return
*/
public int hashCode(String string) {
int result = 0;
// 这个构建hashcode的方式类似于java的string的hashcode方法
// 只是我这里是可以设置的seed,它那里是31
for (int i = 0; i < string.length(); i++) {
char a = string.charAt(i);
int b = seed * a; // 隐式的把字符转换为整数(ASSIC码)
result = result + b;
}
/**
* public static int indexFor(int m, int n){ return m & (n - 1); } public static
* void main(String[] args) { System.out.println("19 与 16 求余 = "+ indexFor(19,
* 16) ); System.out.println("19 与 16 求余 = "+ 19 % 16 ); }
* 此方法中n为2的指数值,则其二进制形式的表示中只存在一个1,其余位都为0, 例如: 0000 1000、0100 0000、0010
* 0000等等。则n-1的二进制形式就为1的位数变为0, 其右边位全变为1,例如16的二进制 0001 0000 -1 = 0000
* 1111测试m为19的二进制 0001 0011 & 0000 1111 = 0000 0011 = 3,地位保留的结果便是余数。此位运算也是
* HashMap中确定元素键(key)值所在哈希数组下标位置的核心方法,此位运算(hash & (length - 1)) 的效率极高于hash %
* length的求余, 所以也解释为什么HashMap的扩容始终为2的倍数(2的指数值)。
*/
// 保证结果在[0,maxLength-1]:equal to 'result % maxLength'
return result & (maxLength - 1);
}
}
public class BloomFilter {
// 构建hash函数的关键字,总共7个
private static final int[] HashSeeds = new int[] { 3, 5, 7, 11, 13, 17, 19 };
// Hash工具类的数组
private static BloomHash[] HashList = new BloomHash[HashSeeds.length];
// BloomFilter的长度,最好为插入数量的10倍,目前为2的20次方,大约100万个
private static final int BloomLength = 1 << 20;
// 对位的操作类,java自带的BitSet,共BloomLength个bit
private BitSet bitSet = new BitSet(BloomLength);
public BloomFilter() {
// 初始化Hash工具类的数组,每个hash工具类的hash函数都不同
for (int i = 0; i < HashSeeds.length; i++) {
HashList[i] = new BloomHash(BloomLength, HashSeeds[i]);
}
}
/**
* 在布隆过滤器中加入值value,在多个hash函数生成的hashcode对应的位置上,置1
*
* @param value字符串,如果为数字,可以自己转化成string
*/
public void addValue(String value) {
for (int i = 0; i < HashSeeds.length; i++) {
// 根据对应的hash函数得到hashcode
int hashcode = HashList[i].hashCode(value);
// 在位图中,将对应的位,设置为1
bitSet.set(hashcode);
}
}
/**
* 在布隆过滤器中,检验是否可能有值value
*
* @param value
* @return 如果返回false,则一定没有<br>
* 如果返回true,就代表有可能有
*/
public boolean existsValue(String value) {
boolean result = true;
for (int i = 0; i < HashSeeds.length; i++) {
// 根据对应的hash函数得到hashcode
int hashcode = HashList[i].hashCode(value);
/**
* 隐式把boolean转换为整数进行按位与运算 “短路” 主要用于逻辑运算符中,即 “ ! && || "这三种运算符 短路 就是知如果左侧的
* 表达式能确定运算后的结果,则不再计算右侧的表达式。 如(1>2)&&(2<3) 明明左侧已经为假 了 我 不用计算右侧我一定知道 此表达是为假
*/
// 将result与对应位置上的0或1 做与运算
// 如果全为1,则result最后为1
// 如果有一个位置上为0,则最后result为0
result = result & bitSet.get(hashcode);
}
return result;
}
}
到了这里,关于区块链基础之密码学及安全技术的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!