简单图论：旅行-Toy模板网

这篇具有很好参考价值的文章主要介绍了简单图论：旅行。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

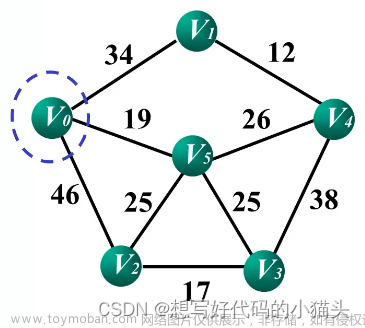
解题思路

最小生成树（Kruskal算法）

不同的的最小生成树：
不是连通的权重最小；
而是连通起始点和终点的路径上最大最小速度比值最小。

如何使得速度比值最小：
问题1：什么情况下比值最小？
$\Rightarrow (1、2、3、4、5）$
问题2：直接基于Kruskal算法构建生成树，算该连通图中的最小比值是否可行？

步骤：
1、按Kruskal算法思路，按路径值排序；
2、从最短边开始基于并查集构建最小生成树；
3、添加边，当起始点和终点连通，计算速度比值；
4、从第二短边重新基于并查集构建最小生成树，重复第三步；
5、直到以所有边开始的最小生成树构建完成，输出比值。文章来源地址https://www.toymoban.com/news/detail-503227.html

AC_Code

# -*- coding: utf-8 -*-
# @Author : BYW-yuwei
# @Software: python3.8.6
from math import gcd
edges = []
def find(x):
    if x==father[x]:
        return x
    father[x] = find(father[x])
    return father[x]
n,m = map(int,input().split())
for i in range(m):
    x,y,u = list(map(int, input().split()))
    edges.append((x,y,u))
s,t = map(int,input().split())
edges.sort(key=lambda x:x[2])
minn = float('inf')
for i in range(m):
    father = [k for k in range(n+10)]
    flag = 0
    j = i
    for j in range(i,m):
        fx = find(edges[j][0])
        fy = find(edges[j][1])
        if fx<fy:
            father[fy]=fx
        else:
            father[fx]=fy
        if find(s)==find(t):
            flag=True
            break
    if flag:
        if edges[j][2]/edges[i][2]<minn:
            minn = edges[j][2]/edges[i][2]
            j1 = edges[j][2]
            j2 = edges[i][2]
if minn==float('inf'):
    print("IMPOSSIBLE")
else:
    if j1%j2==0:
        print(j1//j2)
    else:
        gcds = gcd(j1,j2)
        print('{}/{}'.format(j1//gcds,j2//gcds))