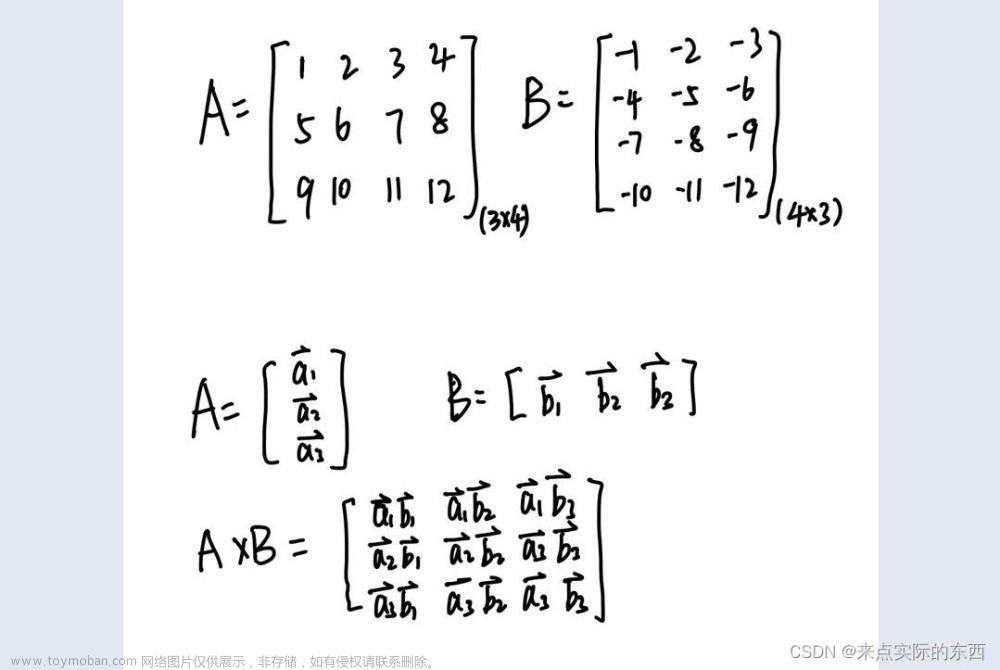
(1)问题
MPI实现矩阵向量:Ab的乘积。其中A:100行100列,b为列向量。
(2)思路
将所有进程分为两部分,rank=0的进程为master节点,其余进程为worker节点。
master节点:
(1)对A,b赋值,同时将b广播出去(这里涉及一个对广播这个函数不太熟悉的点)
(2)对A进行划分,使其被划分为worker数量的份数,并将相应数据发送给相应的工人节点
(3)接收工人节点的计算结果,并对收到的结果及进行一定的处理从而得到最终结果
worker节点:
(1)接受来自master的参数
(2)对接收到的数据进行计算
(3)将结果返回给master
(3)代码
main.cpp:
#include <iostream>
#include "mpi.h"
#include "conf.h"
#include "masterMain.h"
#include "workerMain.h"
#include<string.h>
using namespace std;
MPI_Status status;
int main(int argc, char *argv[]) {
int size, rank;
MPI_Init(&argc, &argv);
char message[20];
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
int a[ROW][COL];
int b[COL], res[COL]; //A为参加运算的矩阵,B为参加运算的向量,result为结果
masterMain mastermain;
workerMain workerMain1;
if (rank == MASTER) {
cout<<"进程0"<<endl;
// cout << "主进程开始对矩阵和向量初始化~" << endl;
for (int i = 0; i < ROW; ++i) {
for (int j = 0; j < COL; ++j) {
a[i][j] = 1;
}
b[i] = 2;
}
}
//广播必须在主进程之外吗?(这里不太理解!!!)
MPI_Bcast(&b, COL, MPI_INT, 0, MPI_COMM_WORLD);
if(rank==MASTER){
mastermain.matrixMuliplication(a,b,ROW,COL,size,res,status);
}else{
workerMain1.workerRun(a,b,ROW,COL,status);
}
MPI_Finalize();
}masterMain.cpp
//
// Created by unbuntu-xcr on 22-10-15.
//
#include "masterMain.h"
#include "conf.h"
#include <iostream>
using namespace std;
void masterMain::masterRun() {
}
/**
*
* @param a 矩阵A
* @param b 向量b
* @param row A的行数
* @param col A的列数
* @param size 参与运算的所有进程数
* @param rank 当前进程号
*/
void masterMain::matrixMuliplication(int a[][100], int *b, int row, int col, int size,int *res,MPI_Status status) {
//master节点任务:首先是初始化矩阵,再分发矩阵,收集各个从节点返回的结果,并放到指定位置
//(1)设置当前进程所需的行
size = size - 1;
int rowPerWorker;
rowPerWorker = row / size;
//master给每个进程传递数据的偏移量
int offset = 0;
cout << "主进程开始对数据进行分发~" << endl;
for (int i = 1; i <= size; ++i) {
rowPerWorker = (i <= row % size ? rowPerWorker + 1 : rowPerWorker);
int count = row * rowPerWorker;
//给从进程传递计算数据
MPI_Send(&offset,1,MPI_INT,i,FROMMASTER,MPI_COMM_WORLD);
MPI_Send(&rowPerWorker,1,MPI_INT,i,FROMMASTER,MPI_COMM_WORLD);
MPI_Send(a[offset], count, MPI_INT, i, FROMMASTER, MPI_COMM_WORLD);
offset+=rowPerWorker;
}
int result[rowPerWorker];
//MASTER接收从进程发来的消息
for (int i = 1; i <= size ; ++i) {
int k=0;
MPI_Recv(&offset,1,MPI_INT,i,FROMWORKER,MPI_COMM_WORLD,&status);
MPI_Recv(&rowPerWorker,1,MPI_INT,i,FROMWORKER,MPI_COMM_WORLD,&status);
MPI_Recv(result,rowPerWorker,MPI_INT,i,FROMWORKER,MPI_COMM_WORLD,&status);
for (int j = offset; j <= offset+rowPerWorker ; ++j) {
res[j]=result[k++];
}
}
cout<<"矩阵向量乘结果为:"<<endl;
for (int i = 0; i < col; ++i) {
cout<<res[i]<<" ";
}
}workerMain.cpp
//
// Created by unbuntu-xcr on 22-10-15.
//
#include "workerMain.h"
#include "conf.h"
void workerMain::workerRun(int a[][100], int *b, int row, int col,MPI_Status status) {
//接收主进程传递的向量,相应矩阵,相应数据,并返回相应计算结果
int offset;
int rowPerWorker;
//接收偏移量
MPI_Recv(&offset,1,MPI_INT,MASTER,FROMMASTER,MPI_COMM_WORLD,&status);
//接收行数
MPI_Recv(&rowPerWorker,1,MPI_INT,MASTER,FROMMASTER,MPI_COMM_WORLD,&status);
//接收矩阵A
MPI_Recv(a,rowPerWorker*col,MPI_INT,MASTER,FROMMASTER,MPI_COMM_WORLD,&status);
int result[rowPerWorker];
// 计算
for (int i = 0; i < rowPerWorker; ++i) {
result[i]=0;
for (int j = 0; j < col; ++j) {
result[i]+=a[i][j]*b[j];
}
}
MPI_Send(&offset,1,MPI_INT,MASTER,FROMWORKER,MPI_COMM_WORLD);
MPI_Send(&rowPerWorker,1,MPI_INT,MASTER,FROMWORKER,MPI_COMM_WORLD);
MPI_Send(result,rowPerWorker,MPI_INT,MASTER,FROMWORKER,MPI_COMM_WORLD);
}
(4)总结
1)为什么要分这么多CPP文件来写?因为想熟悉c++在工程结构上的写法,所以要慢慢开始以这种写法来写
2)问题:mpi_bcast()函数放在master判断条件内为什么就不能将值广播出去?
3)注意:写的时候,先写master发送的,然后写worker接收相应的值,在其进行一定处理并发送给master后,再在master中写接受到相应值之后的操作,这样不至于逻辑混乱文章来源:https://www.toymoban.com/news/detail-503394.html
4)还要注意:send和recv必须保持顺序一致,send谁在前,那么接收谁就在前,不然就会出错文章来源地址https://www.toymoban.com/news/detail-503394.html
到了这里,关于MPI实现矩阵向量乘法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!