用动态规划算法编程实现数字三角形问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了用动态规划算法编程实现数字三角形问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

用动态规划算法编程实现数字三角形问题

前言

一、用动态规划算法编程实现数字三角形问题

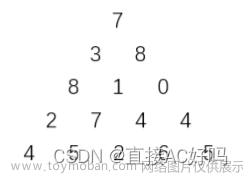
如下所示为一个数字三角形：
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
请编一个程序计算从顶至底的某一条路径，使该路径所经过的数字的总和最大。

思路：建立两个二位数组m（用来存储数字三角形）,sum（用来存储数字三角形中每一个值得路径值）；sum[i] [j]从最后一行开始存储；
如果当前的行数i =数字三角形的行数row，那么这一行中sum的值与m的值对应相同；
如果 i < row ；那么sum[i][j] = max(m[i][j] + sum[i + 1][j], m[i][j] + sum[i + 1][j + 1])；
最终返回sum[1][1]即为所求的最大值。
用动态规划算法编程实现数字三角形问题

二、使用步骤

1.建立求最大值的函数

代码如下（示例）：

int GetPath(int** m, int** sum, int row)
{
	cout << "每一步可沿直线向下或右斜线向下走；1<=三角形行数<=100；三角形中的数字为整数0，1，…，99" << endl;
	int i = row, j = 0;
	if (i == row)
		for (j = 1; j <= i; j++)
		{
			sum[i][j] = m[i][j];
		}
	for (i = row - 1; i > 0; i--)
	{
		for (j = 1; j <= i; j++)
		{
			sum[i][j] = max(m[i][j] + sum[i + 1][j], m[i][j] + sum[i + 1][j + 1]);
		}
	}
	cout << "输出每个值经过计算后的路径值" << endl;
	for (i = 1; i <= row; i++)
	{
		for (j = 1; j <= i; j++)
		{
			cout << setw(3) << sum[i][j];
		}
		cout << endl;
	}
	return sum[1][1];
}

2.读入数据：

用动态规划算法编程实现数字三角形问题

3.完整代码

#include <iostream>
#include <iomanip>
using namespace std;
//比较并返回最大值函数
int max(int a, int b)
{
	if (a > b) return a;
	else return b;
}
//自顶向下计算每一个值的路径值
int GetPath(int** m, int** sum, int row)
{
	cout << "每一步可沿直线向下或右斜线向下走；1<=三角形行数<=100；三角形中的数字为整数0，1，…，99" << endl;
	int i = row, j = 0;
	if (i == row)
		for (j = 1; j <= i; j++)
		{
			sum[i][j] = m[i][j];
		}
	for (i = row - 1; i > 0; i--)
	{
		for (j = 1; j <= i; j++)
		{
			sum[i][j] = max(m[i][j] + sum[i + 1][j], m[i][j] + sum[i + 1][j + 1]);
		}
	}
	cout << "输出每个值经过计算后的路径值" << endl;
	for (i = 1; i <= row; i++)
	{
		for (j = 1; j <= i; j++)
		{
			cout << setw(3) << sum[i][j];
		}
		cout << endl;
	}
	return sum[1][1];
}
int main()
{
	//创建一个数字三角形
	int row;//row行数
	int i = 0, j = 0;
	cout << "请输入三角形行数" << endl;
	cin >> row;
	//动态分配两个二位数组
	int** m = new int* [row];
	int** sum = new int* [row];
	for (i = 1; i <= row; i++)
	{
		m[i] = new int[row];
		sum[i] = new int[row];
	}
	//初始化m数组
	cout << "请输入m[i][j]中的值" << endl;
	for (i = 1; i <= row; i++)
	{
		for (j = 1; j <= i; j++)
			cin >> m[i][j];
	}
	cout << "从顶至底的某一条路径，使该路径所经过的数字的总和最大" << endl;
	int s = GetPath(m, sum, row);
	cout << "从顶至底的某一条路径，该路径所经过的数字的总和最大为" << s << endl;
}