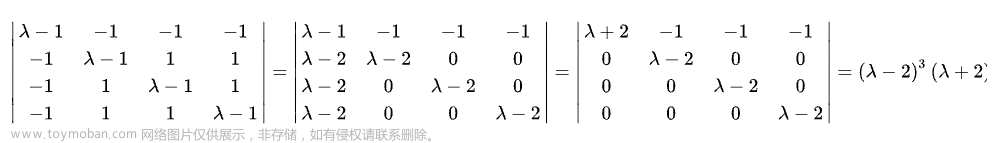计算方法
行列式因子可以由矩阵行列式计算得到,不变因子可以通过计算出的行列式因子间相除得到,初等因子可以由不变因子的分式得到。
信息角度:
其中行列式因子和不变因子包含了特征矩阵的全部信息,而初等因子丢失了秩信息,只有秩和初等因子都相同才能说明特征矩阵等价,而另外两种因子相同即可证明
矩阵相似和等价条件
因此数字矩阵相似的条件:
- λI−A等价于λI−B
- A与B有相同的行列式因子
- A与B有相同的不变因子
- A与B有相同的初等因子
数字矩阵等价:秩相同
多项式矩阵等价的条件:
- 相同的不变因子
- 相同的初等因子
- 相同的秩和初等因子
因为多项式矩阵不一定是满秩的,而数字矩阵的因子是其特征矩阵的相应因子,因此一定是满秩的,可以忽略秩的条件文章来源:https://www.toymoban.com/news/detail-503851.html
补充定义
行列式因子:
不变因子:
初等因子:将不变因子分解后的因式 文章来源地址https://www.toymoban.com/news/detail-503851.html
文章来源地址https://www.toymoban.com/news/detail-503851.html
到了这里,关于关于行列式因子,不变因子,初等因子的理解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!