卡方分布、t分布、F分布-Toy模板网

这篇具有很好参考价值的文章主要介绍了卡方分布、t分布、F分布。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、卡方分布

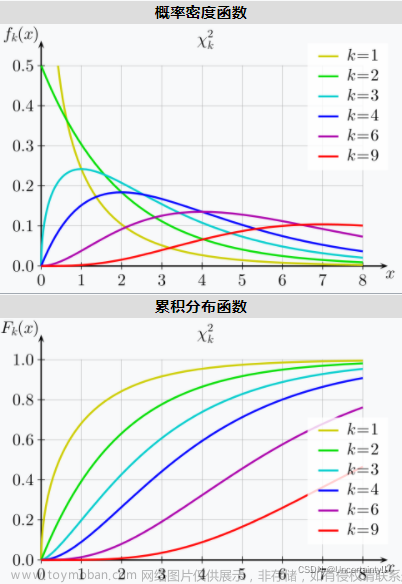
定义：若k个相互独立的随机变量ξ_₁，ξ_₂，…,ξ_k ，均服从标准正态分布（也称独立同分布于标准正态分布），则这k个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）。卡方分布通常用于假设检验，特别是拟合优度的卡方检验。

参数

参数	描述	备注
$k$	$自由度$	$k 是非负数$

概率密度函数
卡方分布、t分布、F分布
其中Γ（•）是Gamma函数，k是自由度。

二、t分布

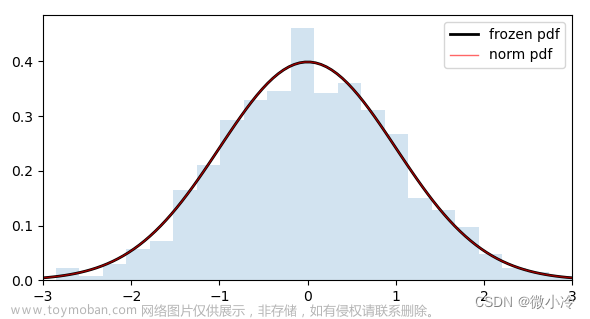
说起t分布，首先要提一句u分布，正态分布（normal distribution）是许多统计方法的理论基础。正态分布的两个参数μ和σ决定了正态分布的位置和形态。为了应用方便，常将一般的正态变量X通过u变换[(X-μ)/σ]转化成标准正态变量u，以使原来各种形态的正态分布都转换为μ=0，σ=1的标准正态分布（standard normaldistribution）,亦称u分布。根据中心极限定理，通过抽样模拟试验表明，在正态分布总体中以固定 n 抽取若干个样本时，样本均数的分布仍服从正态分布，即N（μ，σ）。所以，对样本均数的分布进行u变换，也可变换为标准正态分布N (0,1)。

由于在实际工作中，往往σ(总体方差)是未知的，常用s（样本方差）作为σ的估计值，为了与u变换区别，称为t变换，统计量t 值的分布称为t分布。t分布是一系列曲线，取决于单个参数ν（自由度）。

定义
卡方分布、t分布、F分布
参数