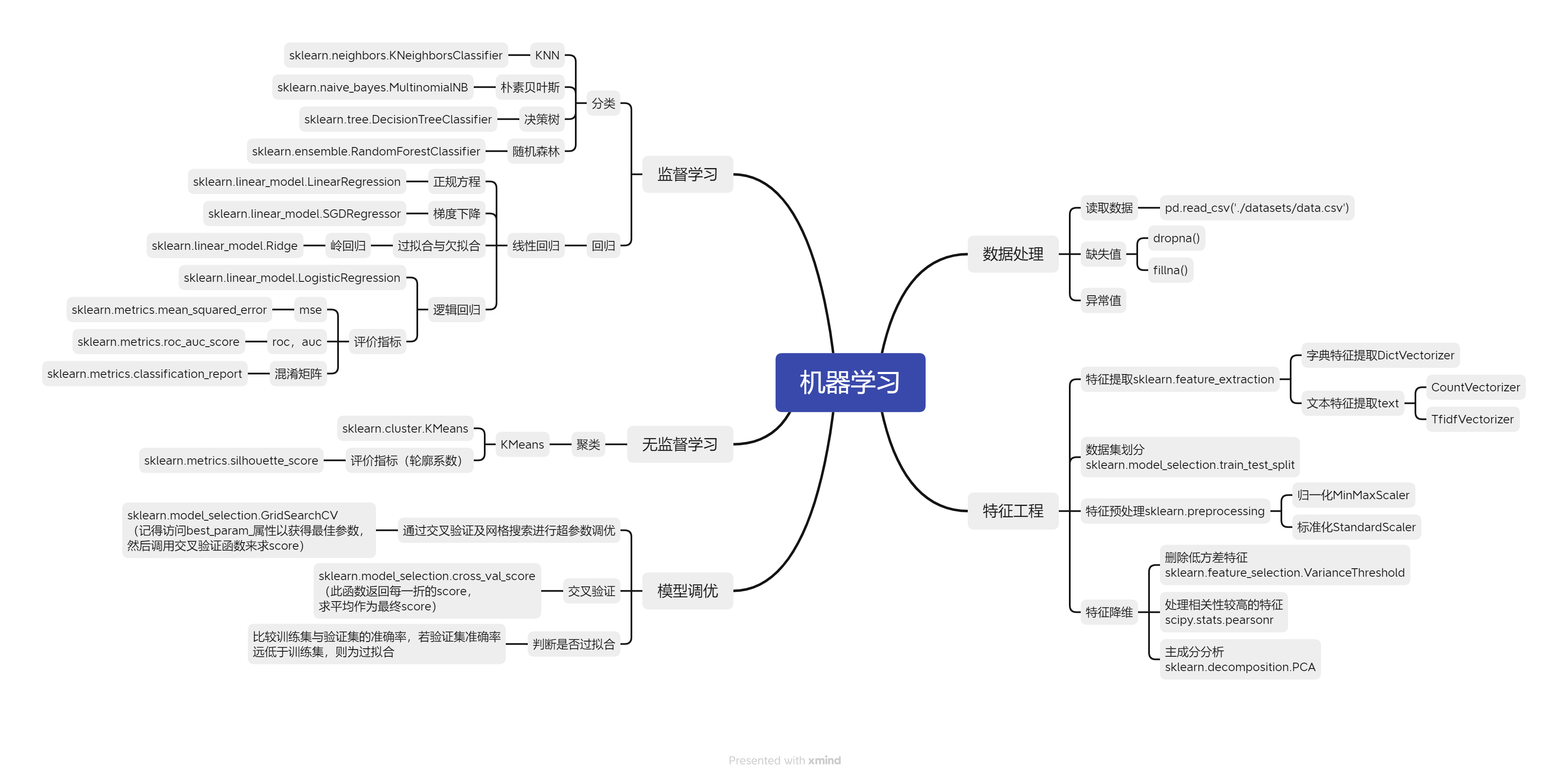
本篇文章旨在让完全不懂的小伙伴对该算法有一个初步认识与理解,只适用于小白
1. 基本概念和基本原理
GBDT(Gradient Boosting Decision Trees,梯度提升决策树)是一种迭代的决策树算法,由多棵决策树组成,所有树的结论累加起来作为最终答案,我们根据其名字来展开推导过程是一种集成学习方法,通过迭代地训练多个决策树,将它们组合成一个强大的预测模型。GBDT以决策树为基分类器,通过梯度提升的方式逐步改善模型的预测能力。
基本原理是通过不断优化损失函数的负梯度来逐步拟合训练数据的残差。每个新的决策树都会尝试去拟合之前模型的残差,从而逐渐减小整体的预测误差。
2. 形式描述
基本形式描述
假设有一个训练数据集 D = { ( x i , y i ) } i = 1 N D = \{(x_i, y_i)\}_{i=1}^N D={(xi,yi)}i=1N,其中 x i x_i xi 是输入特征, y i y_i yi 是对应的输出标签。GBDT的目标是学习一个加法模型 F ( x ) F(x) F(x),使得
F ( x ) = ∑ m = 1 M β m h ( x ; γ m ) F(x) = \sum_{m=1}^M \beta_m h(x; \gamma_m) F(x)=m=1∑Mβmh(x;γm)
其中, h ( x ; γ m ) h(x; \gamma_m) h(x;γm) 是基函数(决策树), γ m \gamma_m γm 是基函数的参数, β m \beta_m βm 是基函数的系数, M M M 是基函数的个数。
目标函数描述
GBDT的目标函数是最小化损失函数的经验风险和正则化项:
L ( F ) = ∑ i = 1 N L ( y i , F ( x i ) ) + ∑ m = 1 M Ω ( h m ) \mathcal{L}(F) = \sum_{i=1}^N L(y_i, F(x_i)) + \sum_{m=1}^M \Omega(h_m) L(F)=i=1∑NL(yi,F(xi))+m=1∑MΩ(hm)
其中, L ( y i , F ( x i ) ) L(y_i, F(x_i)) L(yi,F(xi)) 是损失函数,衡量模型预测与真实标签之间的差异; Ω ( h m ) \Omega(h_m) Ω(hm) 是正则化项,用于控制模型的复杂度。
优化求解描述
GBDT使用前向分步算法来逐步优化目标函数。在每一步中,新增加一个基函数来减小损失函数。
-
初始化模型 F 0 ( x ) F_0(x) F0(x),可以是一个常数,如训练数据的平均值。
-
对于 m = 1 m = 1 m=1 到 M M M:
- 计算当前模型的残差
{
r
i
m
}
i
=
1
N
\{r_{im}\}_{i=1}^N
{rim}i=1N:
r i m = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x) = F_{m-1}(x)} rim=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x) - 拟合一个基函数(决策树) h m ( x ) h_m(x) hm(x),通过拟合残
- 计算当前模型的残差
{
r
i
m
}
i
=
1
N
\{r_{im}\}_{i=1}^N
{rim}i=1N:
差 { r i m } i = 1 N \{r_{im}\}_{i=1}^N {rim}i=1N 得到参数 γ m \gamma_m γm。
- 使用线搜索或其他方法找到基函数的最优系数 β m \beta_m βm,即更新 F m ( x ) = F m − 1 ( x ) + β m h m ( x ) F_m(x) = F_{m-1}(x) + \beta_m h_m(x) Fm(x)=Fm−1(x)+βmhm(x)。
- 最终模型
F
M
(
x
)
F_M(x)
FM(x) 为:
F M ( x ) = F 0 ( x ) + ∑ m = 1 M β m h m ( x ) F_M(x) = F_0(x) + \sum_{m=1}^M \beta_m h_m(x) FM(x)=F0(x)+m=1∑Mβmhm(x)
3. 构造GBDT
构造梯度提升树的步骤如下:
-
准备训练数据集 D = { ( x i , y i ) } i = 1 N D = \{(x_i, y_i)\}_{i=1}^N D={(xi,yi)}i=1N。
-
初始化模型 F 0 ( x ) F_0(x) F0(x),可以是一个常数,如训练数据的平均值。
-
对于 m = 1 m = 1 m=1 到 M M M,重复以下步骤:
- 计算当前模型的残差
{
r
i
m
}
i
=
1
N
\{r_{im}\}_{i=1}^N
{rim}i=1N:
r i m = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x) = F_{m-1}(x)} rim=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x) - 拟合一个基函数(决策树) h m ( x ) h_m(x) hm(x),通过拟合残差 { r i m } i = 1 N \{r_{im}\}_{i=1}^N {rim}i=1N 得到参数 γ m \gamma_m γm。
- 使用线搜索或其他方法找到基函数的最优系数 β m \beta_m βm,即更新 F m ( x ) = F m − 1 ( x ) + β m h m ( x ) F_m(x) = F_{m-1}(x) + \beta_m h_m(x) Fm(x)=Fm−1(x)+βmhm(x)。
- 计算当前模型的残差
{
r
i
m
}
i
=
1
N
\{r_{im}\}_{i=1}^N
{rim}i=1N:
-
最终模型 F M ( x ) F_M(x) FM(x) 为:
F M ( x ) = F 0 ( x ) + ∑ m = 1 M β m h m ( x ) F_M(x) = F_0(x) + \sum_{m=1}^M \beta_m h_m(x) FM(x)=F0(x)+m=1∑Mβmhm(x)
下面给出一个具体的例子来说明:
假设我们有一个回归问题,训练数据集包含以下数据点:
(x1, y1) = (1, 5)
(x2, y2) = (2, 10)
(x3, y3) = (3, 15)
我们的目标是构建一个梯度提升树来拟合这些数据点。
首先,我们初始化模型 F 0 ( x ) F_0(x) F0(x) 为训练数据标签的平均值: F 0 ( x ) = mean ( y 1 , y 2 , y 3 ) = mean ( 5 , 10 , 15 ) = 10 F_0(x) = \text{mean}(y_1, y_2, y_3) = \text{mean}(5, 10, 15) = 10 F0(x)=mean(y1,y2,y3)=mean(5,10,15)=10。
接下来,我们计算残差 { r i m } i = 1 N \{r_{im}\}_{i=1}^N {rim}i=1N:
r1 = -(5 - 10) = 5
r2 = -(10 - 10) = 0
r3 = -(15 - 10) = -5
然后,我们拟合一个基函数(决策树)来拟合这些残差,得到参数 γ m \gamma_m γm。假设拟合得到
的决策树为 h 1 ( x ) h_1(x) h1(x),并且它的叶子节点有两个,分别为区间 [1, 2] 和 [3, 3]。对应的参数为 γ 1 = ( a , b ) = ( 3 , − 2 ) \gamma_1 = (a, b) = (3, -2) γ1=(a,b)=(3,−2)。
接着,我们使用线搜索或其他方法找到基函数的最优系数 β 1 \beta_1 β1。在这个例子中,我们可以通过最小化损失函数 ∑ i = 1 N L ( y i , F m − 1 ( x i ) + β m h m ( x i ) ) \sum_{i=1}^N L(y_i, F_{m-1}(x_i) + \beta_m h_m(x_i)) ∑i=1NL(yi,Fm−1(xi)+βmhm(xi)) 来求解 β 1 \beta_1 β1。具体求解过程略过。
假设最优系数为 β 1 = 1 \beta_1 = 1 β1=1,则更新模型为 F 1 ( x ) = F 0 ( x ) + β 1 h 1 ( x ) F_1(x) = F_0(x) + \beta_1 h_1(x) F1(x)=F0(x)+β1h1(x)。
最终,我们得到模型 F 1 ( x ) F_1(x) F1(x):
F_1(x) = 10 + 1 * 3 (if x in [1, 2])
10 + 1 * (-2) (if x in [3, 3])
可以继续进行更多的迭代,得到更复杂的模型,直到达到预定的迭代次数或满足停止条件。
这就是构造梯度提升树的基本步骤和一个简单示例。文章来源:https://www.toymoban.com/news/detail-505253.html
通过迭代地拟合基函数和更新模型,GBDT能够逐步改善模型的预测能力,并在回归和分类问题中取得出色的表现。文章来源地址https://www.toymoban.com/news/detail-505253.html
到了这里,关于经典机器学习算法之GBDT算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!