智能算法系列之基于粒子群优化的模拟退火算法

这篇具有很好参考价值的文章主要介绍了智能算法系列之基于粒子群优化的模拟退火算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

本篇是智能算法(Python复现)专栏的第四篇文章，主要介绍粒子群优化算法与模拟退火算法的结合，以弥补各自算法之间的不足。

在上篇博客【智能算法系列之粒子群优化算法】中有介绍到混合粒子群优化算法，比如将粒子更新后所获得的新的粒子，采用模拟退火的思想决定是否接受进入下一代迭代。不过啊，本篇也算是混合粒子群优化算法吧，侧重点是将粒子群优化应用在模拟退火算法中，而不是在粒子群优化算法中应用模拟退火算法。

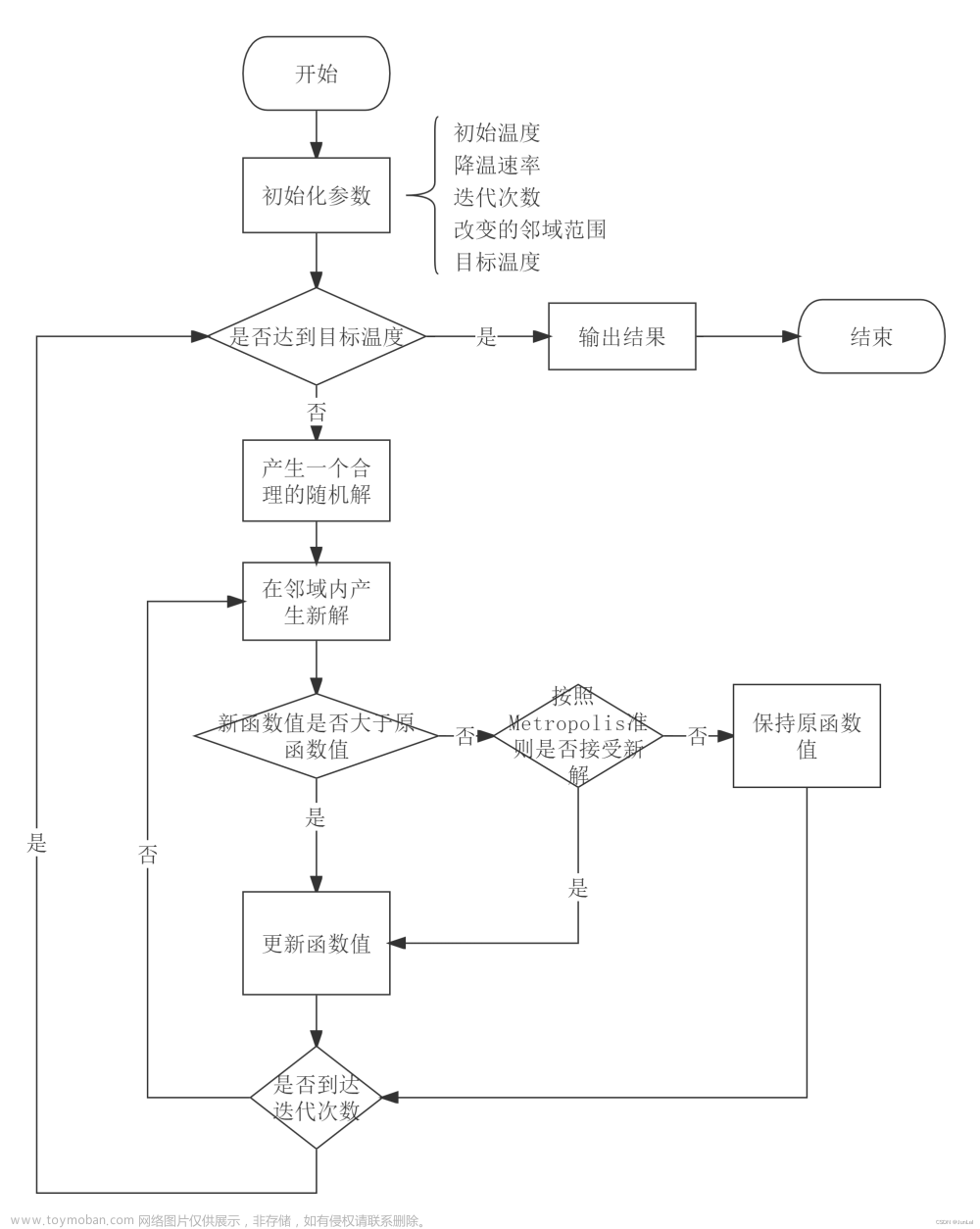
1. 算法结合思路

在这篇博客【智能算法系列之模拟退火算法】中介绍到的模拟退火算法有可以优化的地方，比如在初始解得选择上，默认是随机选择一个解作为初始解，所以想法就来了：如果初始解是一个局部最优解，在此基础之上应用模拟退火算法，那结果肯定会比随机初始解效果好。
如何选择这个初始解或者局部最优解呢，那又有很多算法了，前面介绍的遗传算法和粒子群优化算法都可以使用，本篇就使用粒子群优化来选择初始解。

后续也会在本篇中更新使用遗传算法来选择初始解，不过不打算更新此算法的文章，详细的可以查阅 IALib 库代码。

正如上述所说，本篇并没有在每一代中都应用模拟退火算法（这样的话就是混合粒子群了），而是这样：

智能算法系列之基于粒子群优化的模拟退火算法

2. 问题场景

依然是最值问题，不过将原始的一元函数最值问题换成了二元函数最值问题[复杂度也没增加多少，主要是为了方便可视化]。本次求解三个经典函数的最值：

2.1 Sphere

$f(x, y) = x^2 + y^2$

智能算法系列之基于粒子群优化的模拟退火算法

2.2 Himmelblau

$f(x, y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2$

智能算法系列之基于粒子群优化的模拟退火算法

2.3 Ackley

$exp\bigg[{ -b\sqrt{\frac {x^2 + y^2} {2}} }\bigg] -exp\bigg[ \frac {cos(cx) + cos(cy)} {2} \bigg] + a + e$ 其中， $c=2\pi, e=2.71282$ .

智能算法系列之基于粒子群优化的模拟退火算法

2.4 函数可视化

# -*- coding:utf-8 -*-
# Author:   xiayouran
# Email:    youran.xia@foxmail.com
# Datetime: 2023/3/30 14:22
# Filename: visu_func.py
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


class Visu3DFunc(object):
    def __init__(self, func_name='Sphere'):
        self.func_name = func_name
        self.X = np.linspace(-5, 5, num=200)
        self.Y = np.linspace(-5, 5, num=200)

    @classmethod
    def sphere(cls, x, y):
        """Sphere"""
        return x**2 + y**2

    @classmethod
    def himmelblau(cls, x, y):
        """Himmelblau"""
        return (x**2 + y - 11)**2 + (x + y**2 - 7)**2

    @classmethod
    def ackley(cls, x, y, a=20, b=0.2, c=2*np.pi):
        """Ackley"""
        term1 = -a * np.exp(-b * np.sqrt((x**2 + y**2)/2))
        term2 = -np.exp((np.cos(c*x) + np.cos(c*y))/2)
        return term1 + term2 + a + np.exp(1)

    def draw(self):
        fig = plt.figure()
        # ax = fig.gca(projection='3d')
        ax = Axes3D(fig)
        X, Y = np.meshgrid(self.X, self.Y)

        if self.func_name == 'Sphere':
            Z = self.sphere(X, Y)
        elif self.func_name == 'Himmelblau':
            Z = self.himmelblau(X, Y)
        else:
            Z = self.ackley(X, Y)

        ax.plot_surface(X, Y, Z, cmap=plt.cm.cool)
        ax.contour(X, Y, Z, levels=5, offset=0)
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('Z')
        ax.set_title('{} Function'.format(self.func_name))
        # ax.scatter3D(0, 0, self.sphere(0, 0), s=100, lw=0, c='green', alpha=0.7)
        plt.savefig(self.func_name)

        plt.show()


if __name__ == '__main__':
    # Sphere, Himmelblau, Ackley
    visu_obj = Visu3DFunc(func_name='Sphere')
    visu_obj.draw()

3. 算法实现

# -*- coding:utf-8 -*-
# Author:   xiayouran
# Email:    youran.xia@foxmail.com
# Datetime: 2023/3/30 15:50
# Filename: pso_saa.py
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

from IALib.base_algorithm import BaseAlgorithm
from IALib.particle_swarm_optimization import ParticleSwarmOptimization, Particle
from IALib.simulate_anneal_algorithm import SimulateAnnealAlgorithm
from IALib.mixup.visu_func import Visu3DFunc


__all__ = ['PSO_SAA']


class PSO_SAA(BaseAlgorithm):
    def __init__(self, population_size=100, p_dim=1, v_dim=1, max_iter=500, x_range=(0, 5),
                 t_max=1.0, t_min=1e-3, coldrate=0.9, seed=10086):
        super(PSO_SAA, self).__init__()
        self.__population_size = population_size  # 种群大小
        self.__p_dim = p_dim        # 粒子位置维度
        self.__v_dim = v_dim        # 粒子速度维度
        self.__max_iter = max_iter  # 最大迭代次数
        self.__t_max = t_max  # 初始温度
        self.__t_min = t_min  # 终止温度
        self.__coldrate = coldrate  # 降温速率
        self.saa_best_particle = None   # 模拟退火算法得到的最优解
        self.best_particle = None       # 最优解
        self.__x_range = x_range
        self.__seed = seed
        self.optimal_solution = None

        np.random.seed(self.__seed)

    def problem_function(self, x):
        if self.__p_dim == 1:
            return super().problem_function(x)
        else:
            return Visu3DFunc.sphere(*x)

    def solution(self):
        # PSO
        algo_pso = ParticleSwarmOptimization(population_size=self.__population_size,
                                             p_dim=self.__p_dim, v_dim=self.__v_dim,
                                             max_iter=self.__max_iter, x_range=self.__x_range)
        algo_pso.solution()

        # SAA
        x = algo_pso.global_best_particle.best_position   # 初始解
        while self.__t_max > self.__t_min:
            for _ in range(self.__max_iter):
                x_new = np.clip(x + np.random.randn(), a_min=self.__x_range[0], a_max=self.__x_range[1])
                delta = self.problem_function(x_new) - self.problem_function(x)  # 计算目标函数的值差
                if delta < 0:  # 局部最优解
                    x = x_new   # 直接接受更优解
                else:
                    p = np.exp(-delta / self.__t_max)  # 粒子在温度T时趋于平衡的概率为exp[-ΔE/(kT)]
                    r = np.random.uniform(0, 1)
                    if p > r:  # 以一定概率来接受最优解
                        x = x_new
            self.__t_max *= self.__coldrate

        # optimal solution
        saa_best_particle = Particle()
        saa_best_particle.position = x
        saa_best_particle.best_position = x
        saa_best_particle.fitness = self.problem_function(x)
        self.saa_best_particle = saa_best_particle

        if saa_best_particle.fitness < algo_pso.global_best_particle.fitness:
            self.best_particle = saa_best_particle
        else:
            self.best_particle = algo_pso.global_best_particle

        self.optimal_solution = (self.parse_format(self.best_particle.position),
                                 self.parse_format(self.best_particle.fitness))
        print('the optimal solution is', self.optimal_solution)
        # print('optimal solution:\nposition: {} \nfitness: {}'.format(self.best_particle.best_position,
        #                                                              self.best_particle.fitness))

    def draw(self):
        # PSO
        algo_pso = ParticleSwarmOptimization(population_size=self.__population_size,
                                             p_dim=self.__p_dim, v_dim=self.__v_dim,
                                             max_iter=self.__max_iter, x_range=self.__x_range)
        algo_pso.draw(mixup=True)
        plt.clf()
        x = np.linspace(*self.__x_range, 200)
        plt.plot(x, self.problem_function(x))

        # SAA
        x = algo_pso.global_best_particle.best_position   # 初始解
        while self.__t_max > self.__t_min:
            for _ in range(self.__max_iter):
                # something about plotting
                if 'sca' in globals() or 'sca' in locals():
                    sca.remove()
                sca = plt.scatter(x, self.problem_function(x), s=100, lw=0, c='red', alpha=0.5)
                plt.pause(0.01)

                x_new = np.clip(x + np.random.randn(), a_min=self.__x_range[0], a_max=self.__x_range[1])
                delta = self.problem_function(x_new) - self.problem_function(x)  # 计算目标函数的值差
                if delta < 0:  # 局部最优解
                    x = x_new   # 直接接受更优解
                else:
                    p = np.exp(-delta / self.__t_max)  # 粒子在温度T时趋于平衡的概率为exp[-ΔE/(kT)]
                    r = np.random.uniform(0, 1)
                    if p > r:  # 以一定概率来接受最优解
                        x = x_new
            self.__t_max *= self.__coldrate

        # optimal solution
        saa_best_particle = Particle()
        saa_best_particle.position = x
        saa_best_particle.best_position = x
        saa_best_particle.fitness = self.problem_function(x)
        self.saa_best_particle = saa_best_particle

        if saa_best_particle.fitness < algo_pso.global_best_particle.fitness:
            self.best_particle = saa_best_particle
        else:
            self.best_particle = algo_pso.global_best_particle

        plt.scatter(self.best_particle.best_position, self.best_particle.fitness, s=100, lw=0, c='green', alpha=0.7)
        plt.ioff()
        plt.show()

        self.optimal_solution = (self.parse_format(self.best_particle.position),
                                 self.parse_format(self.best_particle.fitness))
        print('the optimal solution is', self.optimal_solution)
        # print('optimal solution:\nposition: {} \nfitness: {}'.format(self.best_particle.best_position,
        #                                                              self.best_particle.fitness))

    def draw3D(self):
        # PSO
        algo_pso = ParticleSwarmOptimization(population_size=self.__population_size,
                                             p_dim=self.__p_dim, v_dim=self.__v_dim,
                                             max_iter=self.__max_iter, x_range=self.__x_range)
        algo_pso.draw3D(mixup=True)
        plt.clf()
        ax = Axes3D(algo_pso.fig)
        x_ = np.linspace(*self.__x_range, num=200)
        X, Y = np.meshgrid(x_, x_)
        Z = self.problem_function([X, Y])
        ax.plot_surface(X, Y, Z, cmap=plt.cm.cool)
        ax.contour(X, Y, Z, levels=5, offset=0)
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('Z')

        # SAA
        x = algo_pso.global_best_particle.best_position   # 初始解
        while self.__t_max > self.__t_min:
            for _ in range(self.__max_iter):
                # something about plotting
                if 'sca' in globals() or 'sca' in locals():
                    sca.remove()
                sca = ax.scatter3D(*x, self.problem_function(x), s=100, lw=0, c='red', alpha=0.5)
                plt.pause(0.01)

                x_new = np.clip(x + np.random.randn(), a_min=self.__x_range[0], a_max=self.__x_range[1])
                delta = self.problem_function(x_new) - self.problem_function(x)  # 计算目标函数的值差
                if delta < 0:  # 局部最优解
                    x = x_new   # 直接接受更优解
                else:
                    p = np.exp(-delta / self.__t_max)  # 粒子在温度T时趋于平衡的概率为exp[-ΔE/(kT)]
                    r = np.random.uniform(0, 1)
                    if p > r:  # 以一定概率来接受最优解
                        x = x_new
            self.__t_max *= self.__coldrate

        # optimal solution
        saa_best_particle = Particle()
        saa_best_particle.position = x
        saa_best_particle.best_position = x
        saa_best_particle.fitness = self.problem_function(x)
        self.saa_best_particle = saa_best_particle

        if saa_best_particle.fitness < algo_pso.global_best_particle.fitness:
            self.best_particle = saa_best_particle
        else:
            self.best_particle = algo_pso.global_best_particle

        ax.scatter3D(*self.best_particle.best_position, self.best_particle.fitness, s=100, lw=0, c='green', alpha=0.7)
        plt.ioff()
        plt.show()

        self.optimal_solution = (self.parse_format(self.best_particle.position),
                                 self.parse_format(self.best_particle.fitness))
        print('the optimal solution is', self.optimal_solution)
        # print('optimal solution:\nposition: {} \nfitness: {}'.format(self.best_particle.best_position,
        #                                                              self.best_particle.fitness))


if __name__ == '__main__':
    algo = PSO_SAA()
    # algo.draw()
    algo.draw3D()

代码仓库：IALib[GitHub]

本篇代码已同步至【智能算法(Python复现)】专栏专属仓库：IALib
运行IALib库中的PSO-SAA算法：文章来源地址https://www.toymoban.com/news/detail-505487.html

git clone git@github.com:xiayouran/IALib.git
cd examples
python main.py -algo pso_saa		# 2D visu
python main_pro.py -algo pso_saa	# 3D visu

到了这里，关于智能算法系列之基于粒子群优化的模拟退火算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

Toy模板网

智能算法系列之基于粒子群优化的模拟退火算法

前言

1. 算法结合思路

2. 问题场景

2.1 Sphere

2.2 Himmelblau

2.3 Ackley

2.4 函数可视化

3. 算法实现

代码仓库：IALib[GitHub]

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2