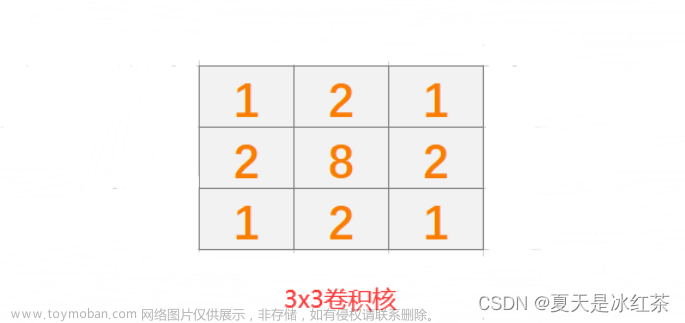
矩阵算法在图像处理、神经网络、模式识别等领域有着广泛的用途。
在矩阵乘法中,A矩阵和B矩阵可以做乘法运算必须满足A矩阵的列的数量等于B矩阵的行的数量。
运算规则:A的每一行中的数字对应乘以B的每一列的数字把结果相加起来。
定义

注意事项
1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。文章来源:https://www.toymoban.com/news/detail-505685.html
3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。文章来源地址https://www.toymoban.com/news/detail-505685.html
导包
<dependency>
<groupId>org.ujmp</groupId>
<artifactId>ujmp-core</artifactId>
<version>0.3.0</version>
</dependency>基本运算
矩阵的创建
//创建4×4矩阵
Matrix dense = DenseMatrix.Factory.zeros(4, 4);
//将第2行和第3列的entry设置为值5.0
dense.setAsDouble(5.0, 2, 3);
//设置一些其他值
dense.setAsDouble(1.0, 0, 0);
dense.setAsDouble(3.0, 1, 1);
dense.setAsDouble(4.0, 2, 2);
dense.setAsDouble(-2.0, 3, 3);
dense.setAsDouble(-2.0, 1, 3);
//在控制台上打印最终的矩阵
System.out.println("矩阵dense:\n"+dense);
1.0000 0.0000 0.0000 0.0000
0.0000 3.0000 0.0000 -2.0000
0.0000 0.0000 4.0000 5.0000
0.0000 0.0000 0.0000 -2.0000矩阵的转置
//矩阵的转置
Matrix transpose = dense.transpose();
System.out.println("矩阵的转置:\n"+transpose);
矩阵的转置:
1.0000 0.0000 0.0000 0.0000
0.0000 3.0000 0.0000 0.0000
0.0000 0.0000 4.0000 0.0000
0.0000 -2.0000 5.0000 -2.0000//再来一个矩阵
Matrix sparse = SparseMatrix.Factory.zeros(4, 4);
sparse.setAsDouble(2.0, 0, 0);
System.out.println("矩阵sparse:\n"+sparse);
矩阵sparse:
2.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000矩阵的求和
//矩阵的求和
Matrix sum = dense.plus(sparse);
System.out.println("矩阵的求和:\n"+sum);
矩阵的求和:
3.0000 0.0000 0.0000 0.0000
0.0000 3.0000 0.0000 -2.0000
0.0000 0.0000 4.0000 5.0000
0.0000 0.0000 0.0000 -2.0000矩阵的相减
//矩阵的相减
Matrix difference = dense.minus(sparse);
System.out.println("矩阵的相减:\n"+difference);
矩阵的相减:
-1.0000 0.0000 0.0000 0.0000
0.0000 3.0000 0.0000 -2.0000
0.0000 0.0000 4.0000 5.0000
0.0000 0.0000 0.0000 -2.0000矩阵的乘法
//矩阵的乘法
Matrix matrixProduct = dense.mtimes(sparse);
System.out.println("矩阵的乘法:\n"+matrixProduct);
矩阵的乘法:
2.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000矩阵的数乘
//矩阵的数乘
Matrix scaled = dense.times(2.0);
System.out.println("矩阵的数乘:\n"+scaled);
矩阵的数乘:
2.0000 0.0000 0.0000 0.0000
0.0000 6.0000 0.0000 -4.0000
0.0000 0.0000 8.0000 10.0000
0.0000 0.0000 0.0000 -4.0000矩阵的逆
//矩阵的逆
Matrix inverse = dense.inv();
System.out.println("矩阵的逆:\n"+inverse);
矩阵的逆:
1.0000 0.0000 0.0000 0.0000
0.0000 0.3333 0.0000 -0.3333
0.0000 0.0000 0.2500 0.6250
-0.0000 -0.0000 -0.0000 -0.5000矩阵的伪逆矩阵
//矩阵的伪逆矩阵
Matrix pseudoInverse = dense.pinv();
System.out.println("矩阵的伪逆矩阵:\n"+pseudoInverse);
矩阵的伪逆矩阵:
1.0000 0.0000 0.0000 0.0000
0.0000 0.3333 0.0000 -0.3333
0.0000 0.0000 0.2500 0.6250
0.0000 0.0000 -0.0000 -0.5000获取矩阵的行数与列数
//获取矩阵的行数与列数
int rowCount = (int) dense.getRowCount();
System.out.println("矩阵dense的行数:"+rowCount);
int columnCount = (int) dense.getColumnCount();
System.out.println("矩阵dense的列数:"+columnCount);
矩阵dense的行数:4
矩阵dense的列数:4数组转矩阵
//数组转矩阵
int[][] a = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9},
};
Matrix arr = DenseMatrix.Factory.importFromArray(a);
System.out.println("数组转矩阵:\n"+arr);
数组转矩阵:
1.0000 2.0000 3.0000
4.0000 5.0000 6.0000
7.0000 8.0000 9.0000矩阵的行列式
//矩阵的行列式
double determinant = dense.det();
System.out.println("矩阵的行列式:"+determinant);
矩阵的行列式:-24.0矩阵的奇异值
//矩阵的奇异值
Matrix[] singularValueDecomposition = dense.svd();
System.out.println("矩阵的奇异值:\n"+ Arrays.toString(singularValueDecomposition));
矩阵的奇异值:
[ 0.0000 0.0000 0.0000 -1.0000
0.3007 -0.9410 0.1553 -0.0000
-0.9222 -0.3284 -0.2041 -0.0000
0.2430 -0.0819 -0.9666 -0.0000
,
6.8481 0.0000 0.0000 0.0000
0.0000 3.1397 0.0000 0.0000
0.0000 0.0000 1.1162 0.0000
0.0000 0.0000 0.0000 1.0000
,
0.0000 0.0000 0.0000 -1.0000
0.1318 -0.8991 0.4174 -0.0000
-0.5387 -0.4184 -0.7313 -0.0000
-0.8322 0.1285 0.5395 -0.0000
]矩阵特征值
//矩阵特征值
Matrix[] eigenValueDecomposition = dense.eig();
System.out.println("矩阵特征值:\n"+ Arrays.toString(eigenValueDecomposition));
矩阵特征值:
[ 1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.4000
0.0000 0.0000 1.0000 -0.8333
0.0000 0.0000 0.0000 1.0000
,
1.0000 0.0000 0.0000 0.0000
0.0000 3.0000 0.0000 0.0000
0.0000 0.0000 4.0000 0.0000
0.0000 0.0000 0.0000 -2.0000
]矩阵LU分解
//矩阵LU分解
Matrix[] luDecomposition = dense.lu();
System.out.println("矩阵LU分解:\n"+ Arrays.toString(luDecomposition));
[ 1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
,
1.0000 0.0000 0.0000 0.0000
0.0000 3.0000 0.0000 -2.0000
0.0000 0.0000 4.0000 5.0000
0.0000 0.0000 0.0000 -2.0000
,
1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
]矩阵分解向量化
//矩阵分解向量化
Matrix[] qrDecomposition = dense.qr();
System.out.println("矩阵分解向量化:\n"+ Arrays.toString(qrDecomposition));
[ -1.0000 0.0000 0.0000 0.0000
0.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 -1.0000
,
-1.0000 0.0000 0.0000 0.0000
0.0000 -3.0000 0.0000 2.0000
0.0000 0.0000 -4.0000 -5.0000
0.0000 0.0000 0.0000 2.0000
]矩阵特征值
//矩阵特征值
Matrix choleskyDecomposition = dense.chol();
System.out.println("矩阵特征值:\n"+ choleskyDecomposition);
矩阵特征值:
1.0000 0.0000 0.0000 0.0000
0.0000 1.7321 0.0000 0.0000
0.0000 0.0000 2.0000 0.0000
0.0000 0.0000 0.0000 0.0000矩阵的拷贝
选取行selectRows(Ret,i) Ret.NEW为深拷贝 Ret.LINK为浅拷贝
// 选取行selectRows(Ret,i) Ret.NEW为深拷贝 Ret.LINK为浅拷贝
Matrix row = dense.selectRows(Calculation.Ret.NEW, 0);
System.out.println("选取行深拷贝:\n"+ row);
选取行深拷贝:
1.0000 0.0000 0.0000 0.0000选取列selectColumns(Ret,i) Ret.NEW为深拷贝 Ret.LINK为浅拷贝
// 选取列selectColumns(Ret,i) Ret.NEW为深拷贝 Ret.LINK为浅拷贝
Matrix column = dense.selectColumns(Calculation.Ret.NEW, 0);
System.out.println("选取列深拷贝:\n"+ column);
选取列深拷贝:
1.0000
0.0000
0.0000
0.0000按第j列进行排序sortrows(Calculation.Ret.NEW, j, boolean)
// 按第j列进行排序sortrows(Calculation.Ret.NEW, j, boolean)
Matrix order = dense.sortrows(Calculation.Ret.NEW, 1, false);
System.out.println("按第j列进行排序:\n"+ order);
按第j列进行排序:
1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 4.0000 5.0000
0.0000 0.0000 0.0000 -2.0000
0.0000 3.0000 0.0000 -2.0000将矩阵的所有数值相加得到的返回值
// 将矩阵的所有数值相加得到的返回值
double accumulation = dense.getValueSum();
System.out.println("将矩阵的所有数值相加得到的返回值:"+ accumulation);
将矩阵的所有数值相加得到的返回值:9.0矩阵的创建
//创建4×4矩阵
Matrix dense = DenseMatrix.Factory.zeros(4, 4);
System.out.println("dense:\n"+dense);
//用0到1之间的随机值创建矩阵
Matrix rand = Matrix.Factory.rand(100, 10);
System.out.println("rand:\n"+rand);
//创建矩阵与-1和-1之间的随机值
Matrix randn = Matrix.Factory.randn(100, 10);
System.out.println("randn:\n"+randn);
//本地主机矩阵
Matrix localhost = Matrix.Factory.localhostMatrix();
System.out.println("localhost:\n"+localhost);
//大稀疏矩阵
SparseMatrix m1 = SparseMatrix.Factory.zeros(1000000, 500000);
System.out.println("m1:\n"+m1);余弦相似矩阵
//余弦相似矩阵
// 创建10个相关列,100行,相关性0.1的矩阵
Matrix correlated = Matrix.Factory.correlatedColumns(100, 10, 0.1);
System.out.println("correlated:\n"+correlated);
// 计算相似度并存储在新矩阵中
// 如果存在,忽略缺失值
Matrix similarity = correlated.cosineSimilarity(Calculation.Ret.NEW, true);
System.out.println("similarity:\n"+similarity);图像矩阵
//图像矩阵
//图片方resources下
InputStream is = ClassLoader.getSystemClassLoader().getResourceAsStream("test.jpg");
//加载图像到矩阵。当然,这也适用于文件
Matrix imageMatrix = new ImageMatrix(is);
System.out.println("imageMatrix:\n"+imageMatrix);
is.close();大稀疏矩阵
//大稀疏矩阵
//创建一个非常大的稀疏矩阵
SparseMatrix m1 = SparseMatrix.Factory.zeros(1000000, 500000);
//设置一些值
m1.setAsDouble(MathUtil.nextGaussian(), 0, 0);
m1.setAsDouble(MathUtil.nextGaussian(), 1, 1);
for (int i = 0; i < 10000; i++) {
m1.setAsDouble(MathUtil.nextGaussian(), MathUtil.nextInteger(0, 1000), MathUtil.nextInteger(0, 1000));
}
System.out.println("m1:\n"+m1);
//创建另一个矩阵
SparseMatrix m2 = SparseMatrix.Factory.zeros(3000000, 500000);
m2.setAsDouble(MathUtil.nextGaussian(), 0, 0);
m2.setAsDouble(MathUtil.nextGaussian(), 1, 1);
for (int i = 0; i < 10000; i++) {
m2.setAsDouble(MathUtil.nextGaussian(), MathUtil.nextInteger(0, 1000), MathUtil.nextInteger(0, 1000));
}
System.out.println("m2:\n"+m2);
// m2矩阵转置后 与m1矩阵相乘法
Matrix m3 = m1.mtimes(m2.transpose());
System.out.println("m3:\n"+m3);提取Excel数据
//提取Excel数据
// find all Excel files in one directory
File[] files = new File("D:/xx/xx").listFiles();
//在一个目录下找到所有Excel文件
assert files != null;
Matrix result = Matrix.Factory.zeros(files.length, 2);
//遍历所有文件
for (int i = 0; i < files.length; i++) {
// 导入文件为矩阵
Matrix m = Matrix.Factory.importFrom().file(files[i]).asDenseCSV();
// 在结果矩阵中存储文件名
result.setAsString(files[i].getName(), i, 0);
if (m.containsString("Invoice"))
提取第10行和第3列的值并存储在result中
result.setAsDouble(m.getAsDouble(10, 3), i, 1);
}
System.out.println("result:\n"+result);图形矩阵
//图形矩阵
//创建一个以字符串为节点,双精度为边的GraphMatrix
GraphMatrix<String, Double> graphMatrix = new DefaultGraphMatrix<String, Double>();
graphMatrix.setLabel("Interface Inheritance Graph");
//收集UJMP中的所有矩阵接口
Class<?>[] classArray = new Class[] { DenseMatrix.class, DenseMatrix2D.class, Matrix.class, Matrix2D.class,
SparseMatrix.class, SparseMatrix2D.class, BaseBigDecimalMatrix.class, BigDecimalMatrix2D.class,
DenseBigDecimalMatrix.class, DenseBigDecimalMatrix2D.class, SparseBigDecimalMatrix.class,
SparseBigDecimalMatrix2D.class, BigIntegerMatrix.class, BigIntegerMatrix2D.class,
DenseBigIntegerMatrix.class, DenseBigIntegerMatrix2D.class, SparseBigIntegerMatrix.class,
SparseBigIntegerMatrix2D.class, BooleanMatrix.class, BooleanMatrix2D.class, DenseBooleanMatrix.class,
DenseBooleanMatrix2D.class, SparseBooleanMatrix.class, SparseBooleanMatrix2D.class,
ByteArrayMatrix.class, ByteArrayMatrix2D.class, DenseByteArrayMatrix.class,
DenseByteArrayMatrix2D.class, SparseByteArrayMatrix.class, SparseByteArrayMatrix2D.class,
ByteMatrix.class, ByteMatrix2D.class, DenseByteMatrix.class, DenseByteMatrix2D.class,
SparseByteMatrix.class, SparseByteMatrix2D.class, CharMatrix.class, CharMatrix2D.class,
DenseCharMatrix.class, DenseCharMatrix2D.class, SparseCharMatrix.class, SparseCharMatrix2D.class,
DoubleMatrix.class, DoubleMatrix2D.class, DenseDoubleMatrix.class, DenseDoubleMatrix2D.class,
SparseDoubleMatrix.class, SparseDoubleMatrix2D.class, FloatMatrix.class, FloatMatrix2D.class,
DenseFloatMatrix.class, DenseFloatMatrix2D.class, SparseFloatMatrix.class, SparseFloatMatrix2D.class,
GenericMatrix.class, GenericMatrix2D.class, DenseGenericMatrix.class, DenseGenericMatrix2D.class,
SparseGenericMatrix.class, SparseGenericMatrix2D.class, IntMatrix.class, IntMatrix2D.class,
DenseIntMatrix.class, DenseIntMatrix2D.class, SparseIntMatrix.class, SparseIntMatrix2D.class,
LongMatrix.class, LongMatrix2D.class, DenseLongMatrix.class, DenseLongMatrix2D.class,
SparseLongMatrix.class, SparseLongMatrix2D.class, ObjectMatrix.class, ObjectMatrix2D.class,
DenseObjectMatrix.class, DenseObjectMatrix2D.class, SparseObjectMatrix.class,
SparseObjectMatrix2D.class, ShortMatrix.class, ShortMatrix2D.class, DenseShortMatrix.class,
DenseShortMatrix2D.class, SparseShortMatrix.class, SparseShortMatrix2D.class, StringMatrix.class,
StringMatrix2D.class, DenseStringMatrix.class, DenseStringMatrix2D.class, SparseStringMatrix.class,
SparseStringMatrix2D.class };
//了解接口如何相互扩展
for (Class<?> c1 : classArray) {
for (Class<?> c2 : classArray) {
if (c2.getSuperclass() == c1) {
// 当class2扩展class1时加边
graphMatrix.setEdge(1.0, c1.getSimpleName(), c2.getSimpleName());
}
for (Class<?> c3 : c2.getInterfaces()) {
if (c1 == c3) {
// 当class2实现class1时加边
graphMatrix.setEdge(1.0, c1.getSimpleName(), c2.getSimpleName());
}
}
}
}
System.out.println("graphMatrix:\n"+graphMatrix);曼德布洛特矩阵
//曼德布洛特矩阵
//从Mandelbrot集合创建一个矩阵
Matrix m = new MandelbrotMatrix();
System.out.println("m:\n"+m);树矩阵
//树矩阵
//创建一个以字符串为元素的树矩阵
TreeMatrix<String> treeMatrix = new DefaultTreeMatrix<String>();
//创建数据
treeMatrix.setRoot("root");
treeMatrix.addChild("root", "child1");
treeMatrix.addChild("root", "child2");
treeMatrix.addChild("root", "child3");
treeMatrix.addChild("child1", "subChild11");
treeMatrix.addChild("child1", "subChild12");
treeMatrix.addChild("child1", "subChild13");
treeMatrix.addChild("child2", "subChild21");
treeMatrix.addChild("child3", "subChild31");
treeMatrix.addChild("child3", "subChild32");
treeMatrix.addChild("subChild12", "subSubChild121");
treeMatrix.addChild("subChild12", "subSubChild122");
treeMatrix.addChild("subSubChild122", "subSubSubChild1221");
System.out.println("treeMatrix:\n"+treeMatrix);
//treeMatrix.showGUI();到了这里,关于矩阵算法之矩阵乘法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!