动态规划(子序列问题) 力扣 c++-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划(子序列问题) 力扣 c++。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

剑指 Offer II 095. 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。

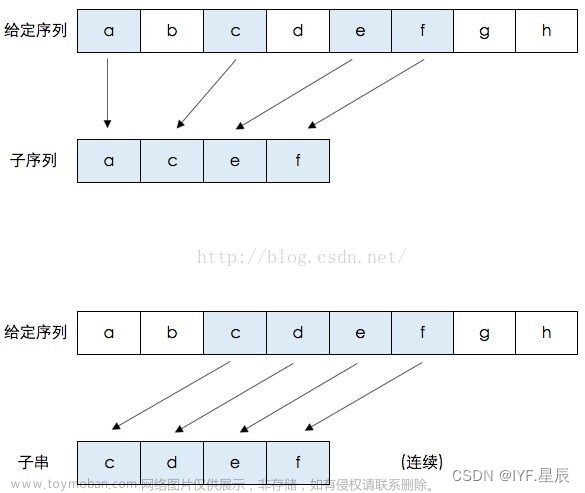
一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。
输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。

思路：字串和子序列是不一样的，子序列不要求是连续的。只要出现在两个字符串中的相对顺序是一样得即可。我们初始化一个二维数组dp来记录最长公共子序列的长度，遍历两个字符串的字符，比较是否相等，如果相等最长公共子序列的长度等于它们前一个位置的最长子序列的长度+1，如果不相等则最长公共子序列的长度等于两个位置分别减去当前字符串的最长公共子序列的较大值。当前位置dp[i][j]的值只与dp[i-1][j-1]、dp[i-1][j]、dp[i][j-1]三个位置的值有关系，最后返回dp[text1.size()][text2.size()]。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        //初始条件:各个长度的子序列与0长度的子序列的最长公共子序列的最大长度为0
        vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));
        for(int i=1;i<=text1.size();i++)
        {
            for(int j=1;j<=text2.size();j++)
            {
                if(text1[i-1]==text2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
思路：我们使用dp来记录记录每个元素结尾的最长递增子序列的长度。计算每个位置的dp值时，我们需要将当前的位置与前面的所有元素进行比较，才能求出当前位置得的最长递增子序列的长度。
dp所有元素值均为1
求5处的dp值
10>9 dp[1]=1;
9>2 dp[2]=3
2<5
10>5 dp[3]=1
9>5 dp[3]=1
2<5 dp[3]=dp[2]+1=3文章来源地址https://www.toymoban.com/news/detail-505739.html

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len=nums.size();
        vector<int> dp(len,1);
        for(int i=1;i<len;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[i]>nums[j])
                {
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }
        }
        return *max_element(dp.begin(),dp.end());
    }
};