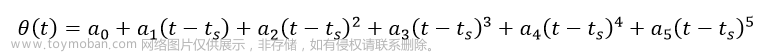Matlab机器人的仿真（八）：绘制机器人运动轨迹（复现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了Matlab机器人的仿真（八）：绘制机器人运动轨迹（复现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

%% 利用标准D-H法建立多轴机器人并作轨迹规划
close all;
clear;
clc;
ks = pi/180;

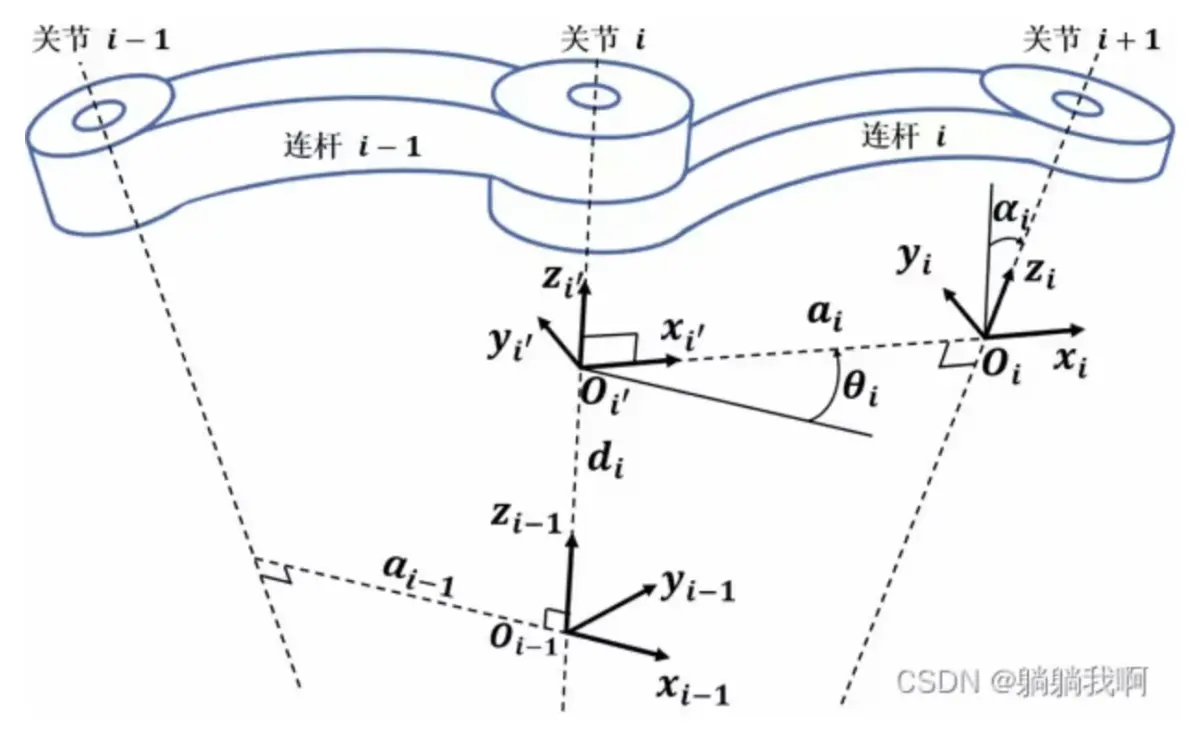
L1 = Link('d', 5, 'a', 5, 'alpha', -pi/2,'offset',0);    %Link 类函数;offset建立初始的偏转角
L2 = Link('d', 0, 'a', 20, 'alpha', 0,  'offset', 0);
L3 = Link('d', 0, 'a', 5, 'alpha', -pi/2,'offset',0);
L4 = Link('d', 20, 'a', 0, 'alpha', pi/2,'offset',0);
L5 = Link('d', 0, 'a', 0, 'alpha', -pi/2,'offset',0);
L6 = Link('d', 10, 'a', 0, 'alpha', 0,   'offset',0);

L1.qlim = [-pi,pi];%利用qlim设置每个关节的旋转角度范围
L2.qlim = [-120,82]*ks;
L3.qlim = [-65,75]*ks;
L4.qlim = [-pi,pi];
L5.qlim = [-120,120]*ks;
L6.qlim = [-pi,pi];
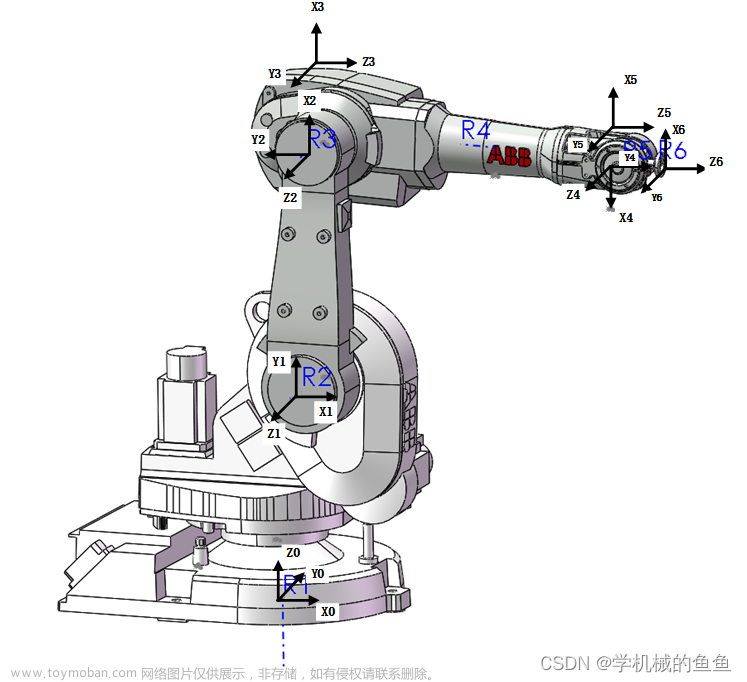
robot=SerialLink([L1,L2,L3,L4,L5,L6],'name','S725');   %SerialLink 类函数
%% 一、运动学轨迹
    ks = pi/180;
    t=[0:0.1:8];%8秒完成轨迹，步长0.1
    
    %方法1、产生位姿矩阵法1：直接给出关节角度
    T1 = robot.fkine([0 0 0 0 0 0]*ks);%生成一个位姿，转弧度制0
    T2 = robot.fkine([70 10 -60 -50 30 30]*ks);%生成一个位姿T2
    
    %方法2、产生位姿矩阵法2：描述位置
%     T1 = transl(0.2,0.2,0.2)*trotx(pi/4);%位移*旋转,创建齐次变换;trotx绕X轴旋转（pi/4角度）
%     T2 = transl(0.2,-0.1,0.1)*trotx(pi/2);
%     T1 = transl(300)*trotz(pi/4);%位移*旋转,创建齐次变换
%     T2 = transl(200)*trotz(pi/2); 
    
    q1 = robot.ikine(T1,'mask',[1 1 1 1 0 1]); %如果是[1 1 1 1 1 0]，则最后一个关节角度一直是0
    q2 = robot.ikine(T2,'mask',[1 1 1 1 0 1],'q0',q1); 
    %关节空间运动规划
    [q,qt,qtt]=jtraj(q1,q2,t);%计算关节空间轨迹函数jtraj,生成三个参数：q为关节角度值，qt为关节角速度值，qtt为关节角加速度值
    
    robot.plot(q,'movie','Motion.gif')%动态绘制轨迹运动
 %% 二、绘出6个关节的角度，角速度，角加速度的信息图
%     figure('name','关节随时间变化图')
%     subplot(3, 1, 1);
%     plot(t, q,'LineWidth',1.5) %绘制关节角随时间的变化
%     grid on;
%     xlabel('时间(s)');ylabel('关节角度(rad)')
%     set(gca,'YLim',[-3 2]);%gca获取当前坐标轴句柄，Y轴的最大，最小值[-3,2]
%     set(gca,'YTick',[-3,-2:2:2]);%设置要显示坐标刻度
%     legend('关节1','关节2','关节3','关节4','关节5','关节6','location','northeastoutside')
% 
%     subplot(3,1,2);
%     plot(t, qt,'LineWidth',1.5) %绘制关节角速度随时间的变化
%     grid on;
%     xlabel('时间(s)');ylabel('角速度(rad/s)')
%     set(gca,'YLim',[-0.3 0.3]);
%     
%     set(gca,'YTick',[-0.3:0.15:0.3]);%设置要显示坐标刻度
%     legend('关节1','关节2','关节3','关节4','关节5','关节6','location','northeastoutside')
% 
%     subplot(3, 1, 3);
%     plot(t, qtt,'LineWidth',1.5) %绘制关节角加速度随时间的变化，如图2
%     grid on;
%     xlabel('时间(s)');ylabel('角加速度(rad/s^2)')
%     set(gca,'YLim',[-0.12 0.12]);
%     set(gca,'YTick',[-0.12:0.06:0.12]);%设置要显示坐标刻度
%     legend('关节1','关节2','关节3','关节4','关节5','关节6','location','northeastoutside')

%% 三、末端点轨迹(x-y-z视图)
%     figure('name','末端点轨迹线')
%     T = robot.fkine(q); %得到笛卡尔轨迹
%     p = transl(T);%进行齐次变换轨迹的位移部分
%     plot3(p(:,1),p(:,2),p(:,3),'LineWidth',1.5) ;grid on;
%     set(gca,'XTick',[-3,-2:2:2]);%设置要显示坐标刻度
%     set(gca,'YTick',[-3,-2:2:2]);%设置要显示坐标刻度
%     set(gca,'ZTick',[-3,-2:2:2]);%设置要显示坐标刻度
%     xlabel('X轴(mm)');ylabel('Y轴(mm)');zlabel('Z轴（mm）');

跑一得出运动轨迹的动图结果：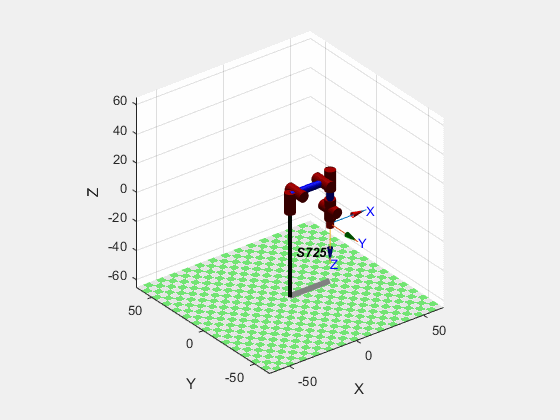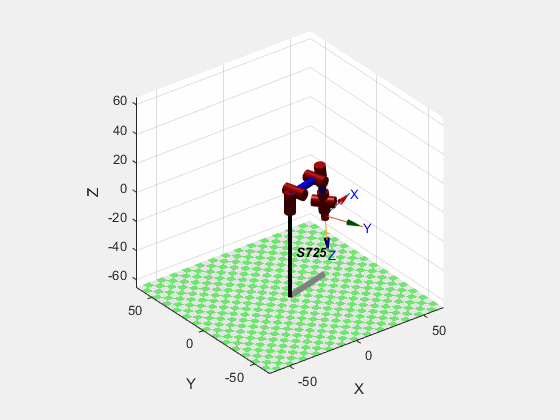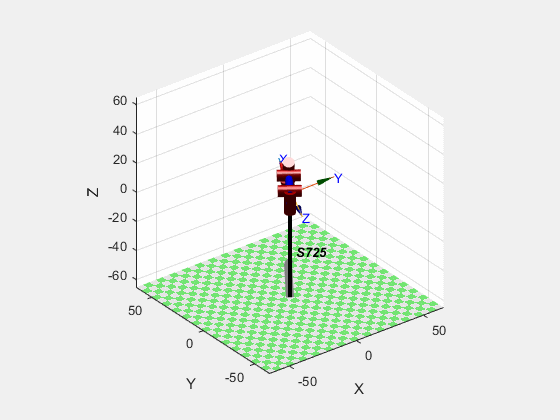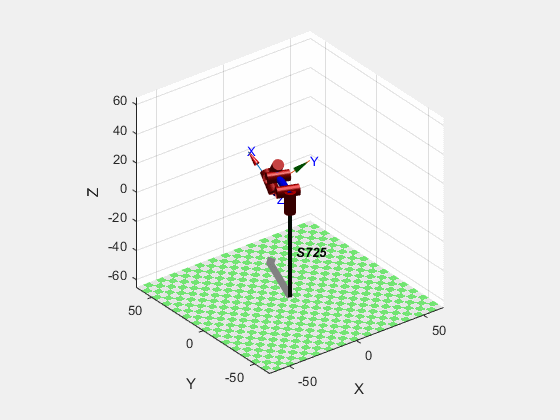
Matlab机器人的仿真（八）：绘制机器人运动轨迹（复现）
跑二得出的绘出6个关节的角度，角速度，角加速度的信息图：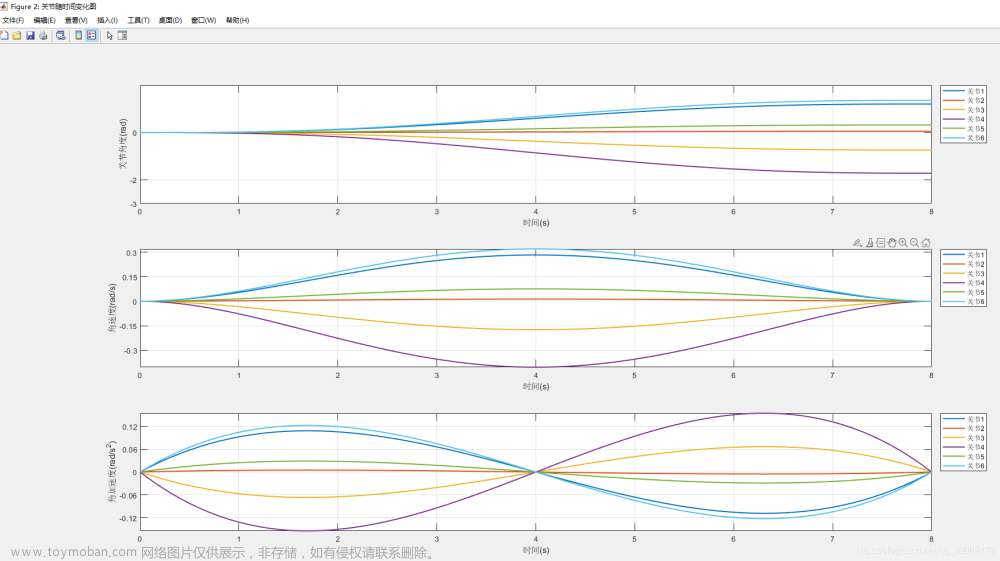

跑三得出的结果：末端点轨迹(x-y-z视图)
文章来源地址https://www.toymoban.com/news/detail-506114.html