【MATLAB图像处理】傅里叶变换--幅度谱、相位谱、逆变换-Toy模板网

这篇具有很好参考价值的文章主要介绍了【MATLAB图像处理】傅里叶变换--幅度谱、相位谱、逆变换。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

fft2() 傅里叶正变换

fftshift() 频谱搬移-直流量（f=0）搬移至频谱中心

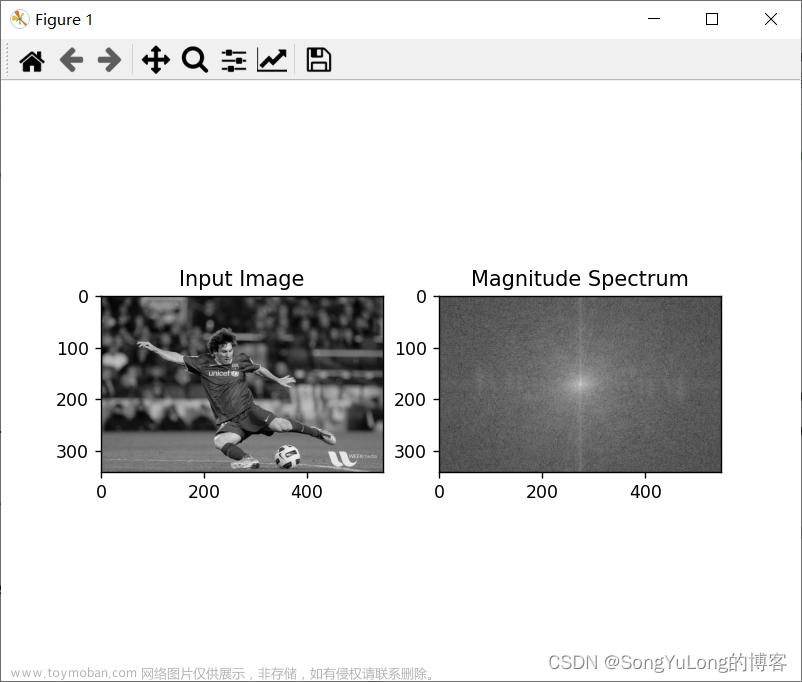
I=imread('exp2.tif');     %读入原图像
I1=I(:,:,1:3);    %四通道转为三通道去掉透明层
I2=rgb2gray(I1);    %对图像进行灰度处理
fftl=fft2(I2);     %二维离散傅里叶变换
sfftl=fftshift(fftl);     %直流分量移到频谱中心
SFFTl=log(sfftl);    %频谱增强
A=log(abs(sfftl));    %对幅度谱进行增强
E=A.^2;    %幅度谱平方得到能量谱
T=angle(sfftl)*180/pi;    %对相位谱进行增强
IA=log(ifft2(ifftshift(sfftl)));    %傅里叶逆变换
subplot(2,3,1);imshow(I2),title('原图');
subplot(2,3,2);imshow(SFFTl,[]),title('频谱');
subplot(2,3,3);imshow(A,[]),title('幅度谱');
subplot(2,3,4);imshow(E,[]),title('能量谱');
subplot(2,3,5);imshow(T),title('相位谱');
subplot(2,3,6);imshow(IA),title('傅里叶逆变换图像');

【MATLAB图像处理】傅里叶变换--幅度谱、相位谱、逆变换

I=imread('exp2.tif');     %读入原图像
I1=I(:,:,1:3);    %四通道转为三通道去掉透明层
I2=rgb2gray(I1);    %对图像进行灰度处理
fftl=fft2(I2);     %二维离散傅里叶变换
sfftl=fftshift(fftl);     %直流分量移到频谱中心
A1=abs(sfftl);    %幅度谱不增强
A=log(abs(sfftl));    %对幅度谱进行增强
T1=angle(sfftl);    %相位谱不增强
T=angle(sfftl)*180/pi;    %对相位谱进行增强
subplot(2,2,1);imshow(A1,[]),title('未增强幅度谱');
subplot(2,2,2);imshow(A,[]),title('已增强幅度谱');
subplot(2,2,3);imshow(T1),title('未增强相位谱');
subplot(2,2,4);imshow(T),title('已增强相位谱');

【MATLAB图像处理】傅里叶变换--幅度谱、相位谱、逆变换

I=imread('exp2.tif');     %读入原图像
I1=I(:,:,1:3);    %四通道转为三通道去掉透明层
I2=rgb2gray(I1);    %对图像进行灰度处理
fftl=fft2(I2);     %二维离散傅里叶变换
sfftl=fftshift(fftl);     %直流分量移到频谱中心
A=log(abs(sfftl));    %对幅度谱进行增强
T=angle(sfftl)*180/pi;    %对相位谱进行增强
IA=log(ifft2(ifftshift(sfftl)));    %傅里叶逆变换
A=log(ifft2(ifftshift(A)));    %傅里叶逆变换
T=log(ifft2(ifftshift(T)));    %傅里叶逆变换
subplot(2,2,1);imshow(I2),title('原图');
subplot(2,2,2);imshow(IA),title('频谱逆变换图像');
subplot(2,2,3);imshow(A),title('幅值逆变换图像');
subplot(2,2,4);imshow(T),title('相位逆变换图像');

【MATLAB图像处理】傅里叶变换--幅度谱、相位谱、逆变换

幅度谱只包含亮度信息（f），逆变换后由于没有位置信息（x，y）导致无法重构图像；相位谱只包含位置信息（x，y），逆变换后由于没有亮度信息（f）导致重构图像只有轮廓没有亮度。而同时利用幅度谱和相位谱可以进行双谱重构恢复出原图像。文章来源地址https://www.toymoban.com/news/detail-506919.html

到了这里，关于【MATLAB图像处理】傅里叶变换--幅度谱、相位谱、逆变换的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！