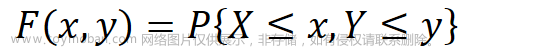一 定义
设D为平面上的有界区域， 其面积为S, 且S>0, 如果二维随机变量(X, Y)的概率密度为
则称(X, Y) 服从区域D上的均匀分布, 记作(X , Y) ~
.
看其两个特殊情形：
-
D为矩形区域
, 
, 此时
-
D为圆形区域， （X, Y）在以原点为圆心、R为半径的圆域上服从均匀分布， 则(X, Y)的概率密度为
二 看例题
设(X, Y) 服从区域D上的均匀分布， 其中D: x ≥y, 0≤x≤1, y≥0, 求P{X+Y ≤ 1}.
解：D区域的示意图如下
D的面积S = 0.5, 所以(X, Y)的概率密度(注意是说密度，没说密度对应的区域)为
事件{X+Y 
1}意味着随机点(X, Y)落在区域 
则文章来源：https://www.toymoban.com/news/detail-507958.html
P{X+Y1} =文章来源地址https://www.toymoban.com/news/detail-507958.html
到了这里，关于概论_第3章_二维随机变量__均匀分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
