哈工大计算机网络课程网络层协议详解之:路由算法概述与链路状态路由算法
在前面的小节中,我们介绍了网络中路由器的路由与转发等功能。我们说作为网络层,从功能上来说,核心功能就是要实现路由和转发。 对于转发来说,实际上就是路由器根据存储的转发表,将目的地址转发到对应的输出链路上去。在这个过程中,完成转发的重要依据,就是转发表,而转发表中的路由信息,就来自于路由算法。 通过路由算法来计算合适的路由信息,存储在转发表中,供后续转发时检索。
总而言之,路由的功能对于网络层来说非常重要,如果没有路由算法来确定路由信息,网络层设备就无法确定接收的数据报应该如何转发到目的地址。
网络抽象:图
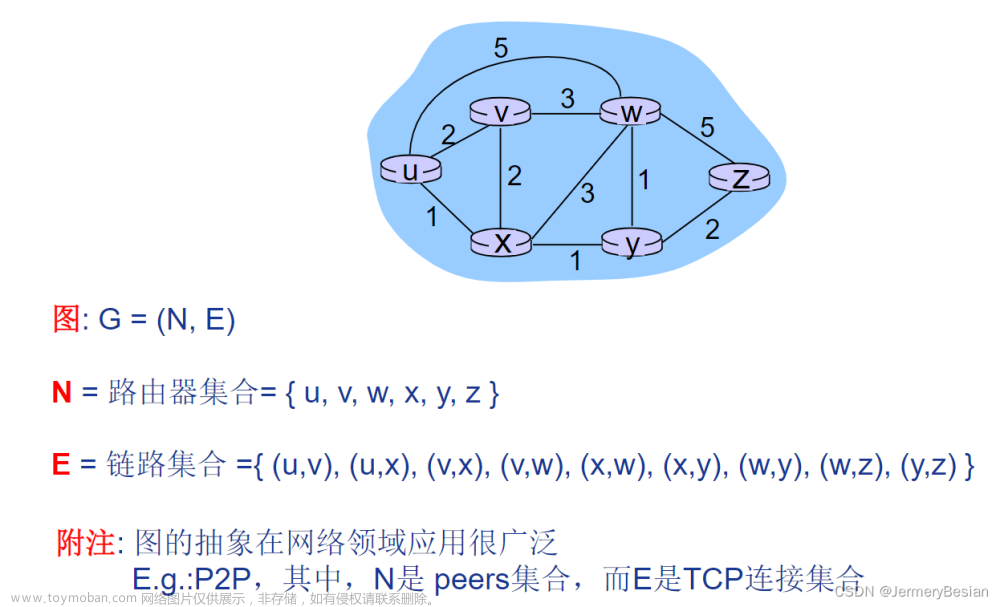
作为各种路由算法,首先都是将网络结构抽象成一个图的结构,如下所示。图的数据结构包含了一系列的节点,用N来表示,节点之间用线连起来表示边,用E来表示。图的抽象在网络领域应用应该说是非常广泛的。

除了顶点和边,还可以对边设定数值,这些数值被成为边的权重。在网络应用中,这些权重被抽象成表示链路传输的代价:cost(x, x’) = 链路(x, x’)的费用,比如图中c(w, z) = 5。实际上,这些权重可以根据网络的不同应用场景来设置,比如可以真实的表示链路的造价成本、带宽的倒数,或者拥塞程度等。
有个上述的权重/费用后,在描述从源主机到目的主机经过的路径费用,就是每条路径的费用之和。

有了上述的目标函数后,路由问题就被抽象成了,如何得到源到目的(如u到z)的最小路径费用是什么?
因此,路由算法就是寻找源到目的之间最小费用路径的算法。
路由算法分类
静态路由 vs 动态路由
静态路由:
-
手工配置。
网络管理员根据对网络的掌握,进行手工配置路由转发规则。
-
路由更新慢。
必须要手动更新
-
优先级高
动态路由:
-
基于路由算法计算得到,路由更新快
网络中的路由器可以快速计算得到新的路由信息,从而快速更新自身的转发表
-
周期性更新
-
及时响应链路费用或网络拓扑变化。
一旦网络链路费用或者拓扑结构发生变化,通过动态路由计算后,能够及时地响应这种变化。
全局信息 vs 分散信息
即路由算法是只需要局部信息,还是需要全局信息。
全局信息:
- 所有路由器掌握完整地网络拓扑和链路费用信息
- 最具有代表性的算法:链路状态(LS)路由算法
分散信息:
- 路由器只掌握物理相连的邻居以及链路费用
- 邻居间信息交换、运算的迭代过程
- 最具代表性的算法:距离向量(DV)路由算法
链路状态路由算法
熟悉数据结构的朋友应该知道,在图结构中求最短路径,一个比较经典的方法就是Dijkstra算法,而链路状态路由算法也恰好就是基于Dijkstra最短路径算法来求解的。
Dijkstra算法在求从一个节点出发,到其他节点的网络最短路径时,需要掌握图的完整拓扑信息和链路费用。 实际上,链路状态路由算法中的链路状态这个词的来历,就反应了我们怎么样保证所有的路由器都能够掌握这张图完整的拓扑信息。
链路状态算法要求每一个路由器,都要构造一个链路状态分组,并进行广播。 这个链路状态分组包含这个路由器与之相连的所有邻居路由器的IP地址,以及与这个路由器直接相连的链路费用。此时,任何路由器都会收集网络中所有其他路由器广播出来的链路状态分组,因此,路由器就可以基于这些链路状态分组中的链路状态信息,构造出完整的网络拓扑结构和链路费用信息。
这样,每个路由器都可以根据它所获取的信息,抽象出完整的网络拓扑结构图和链路费用信息,利用Dijkstra算法计算最短路径。
总结来说就是:
- 所有节点(路由器)掌握网络拓扑和链路费用
- 广播链路状态信息
- 每个路由器获取其他路由器广播的链路状态信息,最终所有节点拥有相同的信息
- 每个路由器根据其获取的信息,抽象出完整的网络拓扑结构和链路费用,计算从一个节点(“源”)到达所有其他节点的最短路径
- 获得该节点的转发表
- 迭代:K次迭代后,得到到达K个目的节点的最短路径(Dijkstra算法的特性)
为了后续对算法描述的便利,先列出使用的符号说明:
- c(x, y):节点x到节点y链路费用,如果x和y不直接相连,则=∞
- D(v): 从源到目的节点v的当前路径费用值
- p(v):沿从源到目的节点v的前序节点
- N‘:已经找到最小费用路径的结点集合
Dijkstra算法
Dijkstra算法的伪代码过程如下所示,与数据结构中图的求最短路径的算法过程是类似的。
首先初始化时将当前节点u放入到N’中,并遍历图中除u节点外的其他节点,如果是u的邻居节点,则计算链路费用D(v),如果不是邻居节点,这u节点到该节点的路径费用初始化为无穷大D(v) = ∞。
接着进入一个循环迭代过程。
首先找出刚刚计算的D(w)中,不在N‘集合中,且D(w)值最小的节点w。
找到后,将该节点w加入到N’中,相当于从邻居节点中,找到链路费用最小的邻居节点。
接下来,再计算w节点的所有不在N’集合中的邻居节点的链路费用。其中,D(v) = min(D(v), D(w) + c(w,v))。这个公式也好理解,因为我始终是要找u节点到其他所有节点的最短路径,所有每个D(v)保存的都应该是节点u到当前节点的最小值。
最后重复这个过程,直到所有的节点都包含在了N‘集合中,表示已经找到了所有其他节点的最短路径。
Dijkstra算法示例
假设有下图的网络拓扑结构,我们计算节点u到网络中其他各节点的最短路径。
-
首先将节点u加入到已确定最短路径节点集合N’,计算节点u的邻居节点的路径长度D(X)=5、D(W)=3、D(V)=7,并初始化其他节点的D(y)、D(Z) = ∞
-
选取节点u邻居节点的最短路径D(w) = 3,的节点W加入N‘,继续计算w节点的邻居节点(不在集合N’中邻居节点)的路径长度。
这里节点x在u->w->x的路径下D(x) = 7 < 原先从u->x的路径D(x)=5,所以仍然保留D(x) = 5。这也就是上面公式D(v) = min(D(v), D(w) + c(w,v))。而对于节点v来说,路径u->w->v的D(v) = 6 < 原先从u->v的路径D(v) = 7,因此节点v的最短路径D更新为D(v) = 6。
-
在节点w的邻居节点中,路径最短的节点是v,加入集合N‘中,继续计算v节点的邻居节点的路径长度。
-
同样的,这次取的邻居节点的最短路径是节点y,加入集合N’,此时D(y) = 10。继续计算y节点的邻居节点的路径长度。
-
最短路径是节点z,加入集合N‘,此时D(z) = 12。
-
最终,集合N’已经包含网络中所有节点,则遍历结束,此时节点对应的D(x)保存的就是节点u到当前节点的最短路径。
整体的流程记录如下图所示,每次红圈圈选出来的都是每一步的最短路径节点。

示例2,整理的流程步骤跟上述类似。

在示例2中我们最终可以得到的节点u到网络中其他各节点的最短路径树为:

这个最短路径树获取后,对于节点u来说,会把这个信息反映到最终的转发表中:

利用这个转发表,路由器u就知道如果需要将数据报发送到网络中其他节点时,应该走什么样的最短路径。比如要把数据送往路由器v,就可以通过u->v这个接口转发出去,如果要把数据送往路由器x、y、w、z,则都是通过u->x的接口转发出去。这就实现了基于Dijkstra算法的链路状态路由算法。
Dijkstra算法讨论
算法复杂性:n个节点文章来源:https://www.toymoban.com/news/detail-507962.html
- 每次迭代:需要检测所有不在集合N‘中的节点w
- n(+1)/2次比较:时间复杂度O(n²)
- 更高效的实现:O(nlogn)
链路状态路由算法的基础是每个节点都需要获取到整个网络的完整拓扑结构,这个在网络规模比较大时,很难适用。因此,接下来我们还会继续介绍距离向量路由算法,以及层次化路由算法。文章来源地址https://www.toymoban.com/news/detail-507962.html
到了这里,关于哈工大计算机网络课程网络层协议详解之:路由算法概述与链路状态路由算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!