Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

北太天元（Baltamatica）简介

北太天元（Baltam）是一款对标矩阵实验室（Matlab）的国产通用科学计算软件，目前版本还在持续更新迭代中，并在国内不断提升知名度，营造良好的生态社区氛围。在很多外行、内行人都不看好Matlab国产化，甚至面对工业软件国产化的项目“谈虎色变”的形势下，北太天元横空出世，带着一股国人特有的骨气踏实迈进，此举可谓意义重大。

北太天元官网：baltamatica.com
卢朓-研发北太天元的意义

Baltamatica 复现基于Matlab的旅行商问题

研0开学前还比较自由，由于已经决定研二期间参加一次数学建模研赛（在此立flag，三牌楼通院/物联网有意向组队的可以加个v噢），并听说现在很多数模竞赛都鼓励学生使用北太天元作为编程仿真工具，就尝试下载了 Baltamatica 2.3.1 想跑个demo看看，但实际上遇到的问题其实比想象的要多，甚至官方给出的example中也会有运行时闪退的情况。最后还是花了个把小时才把之前用matlab写的模拟退火TSP问题完整复现为 Baltamatica 版本，当结果都能正常运行时，感觉还是挺惊奇的，向国内有这样一支热血的研发团队致敬！

Matlab版本：Matlab【旅行商问题】—— 基于模拟退火算法的无人机药品配送路线最优化

Matlab【路径规划】—— 无人机药品配送路线最优化

问题描述

某市引进一架专业大型无人机用于紧急状态下的药品投递，每个站点只能投放一次，可选择指派任意站点的无人机起飞出发完成投递任务，但必须在配送完毕后返回原来的站点。站点地理位置坐标（单位为公理）如下图所示。每个站点及容纳的病人数量见附件data_all.mat数据，现要求通过数学建模，在保证速度和优先救治病人数量多的站点前提下，提供药品紧急配送策略，具体问题如下：

请制订无人机的飞行路线，使尽可能多的病人尽早得到救治。
Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题

模拟退火算法

模拟退火算法是一种基于随机搜索的优化算法，其灵感来源于铸炼工具时，先将固体加热至高温后缓慢冷却，就能使固体获得更好的韧性（可弯折），其原理是退火降温过程中固体内部的晶粒能够以较低的能量重新排列，模拟退火算法就是模拟加热后的退火过程。它的目标是在解空间中寻找全局最优解或接近最优解的解（不一定能找到全局最优，可能是比较接近全局最优的局部最优）。

在模拟退火算法中，首先随机生成一个初始解，然后通过一系列的状态转移来搜索更优的解。状态转移的过程（即马尔可夫链）中，算法会引入一个控制参数（温度），使得算法在搜索过程中能够以一定的概率接受劣解，从而避免陷入局部最优解。随着搜索的进行，温度会逐渐降低，接受劣解的概率也会逐渐减小，最终收敛到全局最优解或接近最优解。

Metropolis准则

模拟退火的主要思想是:在搜索区间随机游走（即随机选择点)，再利用Metropolis抽样准则，使随机游走逐渐收敛于局部最优解。而温度是Metropolis算法中的一个重要控制参数，可以认为这个参数的大小控制了随机过程向局部或全局最优解移动的快慢。

Metropolis准则是用于决定在Metropolis算法中是否接受状态转移的准则。根据Metropolis准则，状态转移被接受的概率为1或 $e x p (- Δ E / T))$ ，其中ΔE表示当前状态与下一个状态的能量差，T表示当前的温度。

具体来说，
如果ΔE小于0，即下一个状态的能量比当前状态更低，那么状态转移被接受（被接受的概率为1）；
如果ΔE大于0，即下一个状态的能量比当前状态更高，那么状态转移被接受的概率为 $e x p (- Δ E / T)$ （即有一定概率放弃状态转移）.

当温度较高时，接受劣解的概率较高，有助于跳出局部最优解；当温度较低时，接受劣解的概率较低，有助于收敛到全局最优解。

Metropolis准则的核心思想是通过接受概率来探索状态空间，从而达到对系统的采样和模拟。这种准则在Metropolis算法中起到了重要的作用，使得算法能够在搜索过程中兼顾探索和利用，从而更好地找到系统的平衡分布。

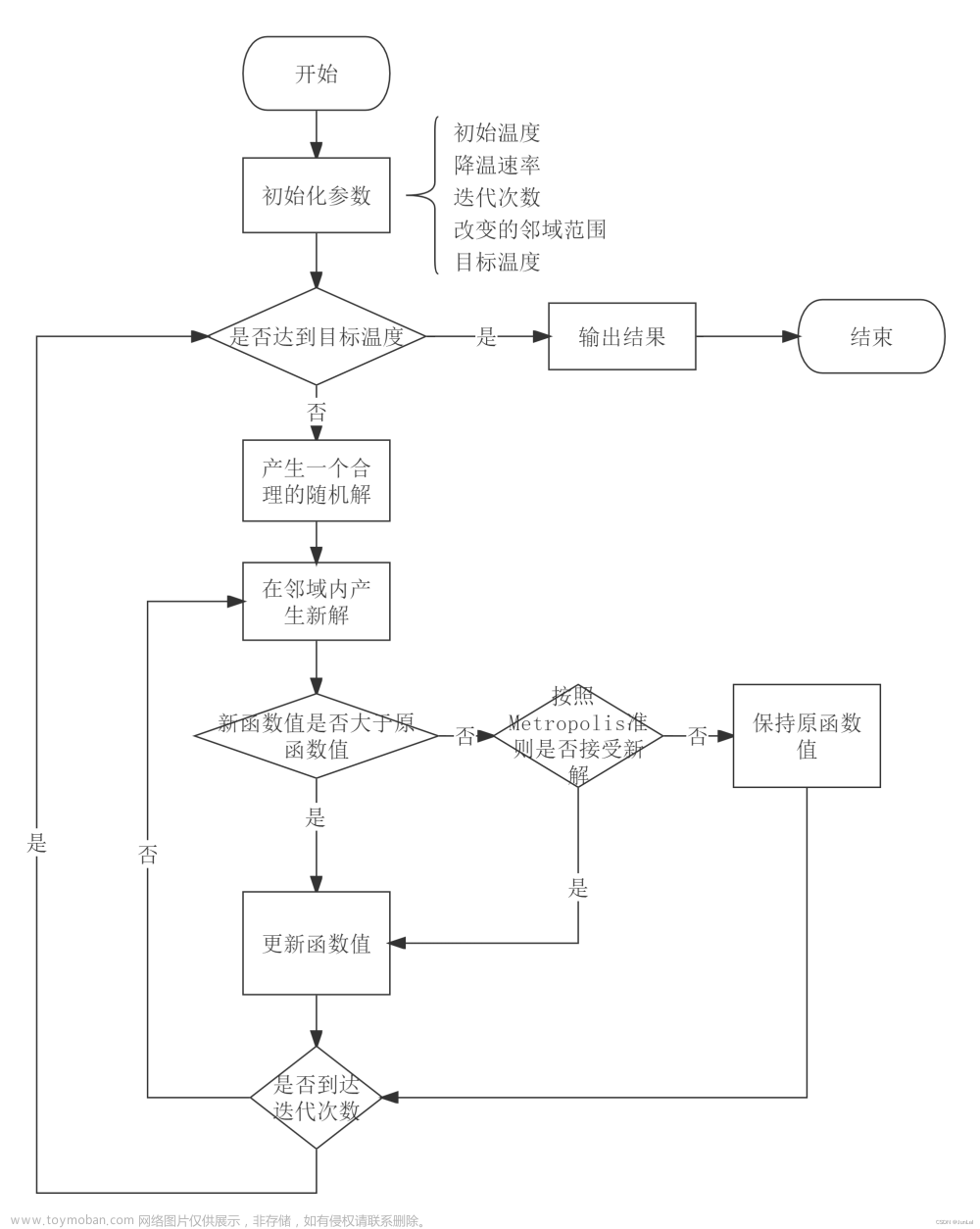
算法流程图：

Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题

Demo1：只考虑累计距离，通过模拟退火算法求解最短路径

先通过Demo1，感受一下模拟退火算法处理旅行商问题的优化过程。

matlab代码：

clc,clear,close all;
%% ------------------------------------------------------------------------
%加载数据
load data_all.mat
data = zeros(25,2);
data(:,1) = data_all(:,2);
data(:,2) = data_all(:,3);
%% ------------------------------------------------------------------------
%模拟退火参数设置
n = size(data,1);  %站点数量
T = 100*n;         %初始温度
L = 100;           %马尔可夫链长度
K = 0.99;          %衰减参数
%% ------------------------------------------------------------------------
%站点坐标结构体
cp = struct([]);
for i = 1:n
    cp(i).x = data(i,1);
    cp(i).y = data(i,2);
end
le = 1;            %迭代次数
len(le) = funcp(cp,n);
figure(1);
while T > 0.001    %停止迭代温度
    %多次迭代扰动，温度降低前多次实验
    for i = 1:L
        %计算原路线距离
        len1 = funcp(cp,n);
        %产生随机扰动
        %随机置换两个不同站点的坐标
        p1 = floor(1+n*rand());
        p2 = floor(1+n*rand());
        while p1 == p2
            p1 = floor(1+n*rand());
            p2 = floor(1+n*rand());
        end
        tmp_cp = cp;
        tmp = tmp_cp(p1);
        tmp_cp(p1) = tmp_cp(p2);
        tmp_cp(p2) = tmp;
        %% ----------------------------------------------------------------
        %计算新路线总距离
        len2 = funcp(tmp_cp,n);
        %% ----------------------------------------------------------------
        %新老距离的差值，相当于能量
        delta_e = len2-len1;
        %% ----------------------------------------------------------------
        %若新路线好于旧路线，用新路线代替旧路线
        if delta_e < 0
            cp = tmp_cp;
        else
            %依概率选择是否接收新解
            if exp(-delta_e/T) > rand()
                cp = tmp_cp;
            end
        end
    end
    le = le+1;
    %% --------------------------------------------------------------------
    %计算新路线距离
    len(le) = funcp(cp,n);
    %温度不断下降
    T =T*K;
    for i = 1:n-1
        plot([cp(i).x, cp(i+1).x], [cp(i).y, cp(i+1).y], "o-","LineWidth", 1.2);
        hold on;
        grid on;
    end
    plot([cp(n).x, cp(1).x], [cp(n).y, cp(1).y],'ro--',"LineWidth", 1.5);
    title(['优化最短距离：', num2str(len(le))]);
    disp(['优化最短距离：', num2str(len(le))])
    hold off;
    pause(0.001);
end
figure(2);
plot(len, 'LineWidth', 1.1)
grid on;
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进行曲线')
disp('优化结束')
%% ------------------------------------------------------------------------
%计算路线总长度函数
function len = funcp(cp,n)
len = 0;
for i = 1:n-1
    len = len+sqrt((cp(i).x-cp(i+1).x)^2+(cp(i).y-cp(i+1).y)^2);  %累计欧氏距离
end
len = len+sqrt((cp(n).x-cp(1).x)^2+(cp(n).y-cp(1).y)^2);
end

Baltam代码：

clc;
clear;
clf;
%% ------------------------------------------------------------------------
%加载数据
cp_x = load('cp_x.mat');
cp_y = load('cp_y.mat');
data = zeros(25,2);
%% ------------------------------------------------------------------------
%模拟退火参数设置
n = size(data,1);  %站点数量
indx = 1:n;
T = 100*n;         %初始温度
L = 100;           %马尔可夫链长度
K = 0.99;          %衰减参数
%% ------------------------------------------------------------------------
%站点坐标结构体
cp = struct('x',cp_x.cp_x,'y',cp_y.cp_y);
cpx = cp.x;
cpy = cp.y;
xx = cp.x;
yy = cp.y;
lem = 1;            %迭代次数
len(lem) = funcp(cpx,cpy,n);
figure('Color','white');
while T > 0.001    %停止迭代温度
    %多次迭代扰动，温度降低前多次实验
    for cnt = 1:L
        %计算原路线距离
        len1 = funcp(cpx,cpy,n);
        %产生随机扰动
        %随机置换两个不同站点的坐标
        p1 = floor(1+n*rand());
        p2 = floor(1+n*rand());
        while p1 == p2
            p1 = floor(1+n*rand());
            p2 = floor(1+n*rand());
        end
        tmp_cpx = cpx;
        tmpx = tmp_cpx(p1);
        tmp_cpx(p1) = tmp_cpx(p2);
        tmp_cpx(p2) = tmpx;
        tmp_cpy = cpy;
        tmpy = tmp_cpy(p1);
        tmp_cpy(p1) = tmp_cpy(p2);
        tmp_cpy(p2) = tmpy;
        %% ----------------------------------------------------------------
        %计算新路线总距离
        len2 = funcp(tmp_cpx,tmp_cpy,n);
        %% ----------------------------------------------------------------
        %新老距离的差值，相当于能量
        delta_e = len2-len1;
        %% ----------------------------------------------------------------
        %若新路线好于旧路线，用新路线代替旧路线
        if delta_e < 0
            cpx = tmp_cpx;
            cpy = tmp_cpy;
        else
            %依概率选择是否接收新解
            if exp(-delta_e/T) > rand()
                cpx = tmp_cpx;
                cpy = tmp_cpy;
            end
        end
    end
    lem = lem+1;
    %% --------------------------------------------------------------------
    %计算新路线距离
    len(lem) = funcp(cpx,cpy,n);
    disp(["优化最短距离：", num2str(len(lem))])
    disp(["起点坐标：", num2str([cpx(1), cpy(1)])])
    disp(["最后一个站点坐标：", num2str([cpx(n), cpy(n)])])
    %温度不断下降
    T =T*K;
    for jj = 1:n-1
        plot([cpx(jj), cpx(jj+1)], [cpy(jj), cpy(jj+1)], "o-","LineWidth", 1.2);
        hold on;
    end
    for kk = 1:n
        text(xx(kk)+0.5,yy(kk)+0.75,num2str(indx(kk)),'fontsize',10);
    end
    plot([cpx(n), cpx(1)], [cpy(n), cpy(1)],'r-.',"LineWidth", 1.5);
    axis([0,120,-2,58]);
    title(['优化最短距离：', num2str(len(lem))]);
    hold off;
end
figure('2');
plot(len, 'LineWidth', 1.1)
axis([0,length(len),floor(min(len)),ceil(max(len))])
xlabel("迭代次数")
ylabel("目标函数值")
title('适应度进行曲线')
disp("优化结束")
%% ------------------------------------------------------------------------
计算路线总长度函数
function len = funcp(cpx,cpy,n)
tar = 0;
len = 0;
for ii = 1:n-1
    len = len+sqrt((cpx(ii)-cpx(ii+1))^2+(cpy(ii)-cpy(ii+1))^2);
end
len = len+sqrt((cpx(n)-cpx(1))^2+(cpy(n)-cpy(1))^2);
end

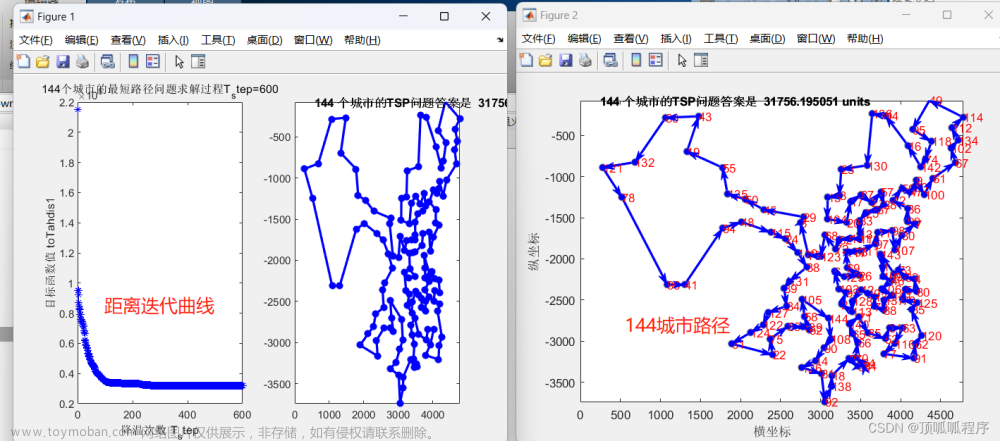
北太天元运行中的效果：

Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题

其实可以看出Baltam的代码风格已尽可能地贴近Matlab，这对于从matlab转入baltam来说是非常重要的，但还不足以达到直接把Matlab的代码、工程导入进去一键运行。

matlab求解情况：

由于模拟退火算法的优化过程具有随机性，所以得到的解不一定就是全局最优，但肯定比瞎猜一个局部最优要好。可以重复运行几次程序，观察最优解的变化，正常应该差距不大。

最优解之一：
Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题
只考虑距离的情况不用考虑路线顺序，因为正反走都是一样的距离。

适应度进行曲线：

Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题
可见适应度随着退火过程逐渐趋于稳定的最优解，算法具有收敛性。

Demo2：考虑每个站点的病人数量，优先给病人数量多的站点配送，同时兼顾累计最短距离

新建目标值变量tar，tar包含了累计距离变量len的大小，且加入了病人数量这个变量var，并乘以权重10，用1000-var是为了反向考虑优化过程中需要使得目标值tar越来越小：

tar = tar+sqrt((cp(i).x-cp(i+1).x)^2+(cp(i).y-cp(i+1).y)^2)+10*(1000-var(i));

matlab代码：

clc,clear,close all;
%% ------------------------------------------------------------------------
%加载数据
load data_all.mat
data = zeros(25,2);
data(:,1) = data_all(:,2);
data(:,2) = data_all(:,3);
var = data_all(:,4);
%% ------------------------------------------------------------------------
%模拟退火参数设置
n = size(data,1);  %站点数量
T = 100*n;         %初始温度
L = 100;           %马尔可夫链长度
K = 0.99;          %衰减参数
%% ------------------------------------------------------------------------
%站点坐标结构体
cp = struct([]);
for i = 1:n
    cp(i).x = data(i,1);
    cp(i).y = data(i,2);
end
le = 1;            %迭代次数
[tar(le), len(le)] = funcp(cp,n);
figure(1);
while T > 0.001    %停止迭代温度
    %多次迭代扰动，温度降低前多次实验
    for i = 1:L
        %计算原路线距离
        [tar1, ~] = funcp(cp,n);
        %产生随机扰动
        %随机置换两个不同站点的坐标
        p1 = floor(1+n*rand());
        p2 = floor(1+n*rand());
        while p1 == p2
            p1 = floor(1+n*rand());
            p2 = floor(1+n*rand());
        end
        tmp_cp = cp;
        tmp = tmp_cp(p1);
        tmp_cp(p1) = tmp_cp(p2);
        tmp_cp(p2) = tmp;
        %% ----------------------------------------------------------------
        %计算新路线总距离
        [tar2, ~] = funcp(tmp_cp,n);
        %% ----------------------------------------------------------------
        %新老距离的差值，相当于能量
        delta_e = tar2-tar1;
        %% ----------------------------------------------------------------
        %若新路线好于旧路线，用新路线代替旧路线
        if delta_e < 0
            cp = tmp_cp;
        else
            %依概率选择是否接收新解
            if exp(-delta_e/T) > rand()
                cp = tmp_cp;
            end
        end
    end
    le = le+1;
    %% --------------------------------------------------------------------
    %计算新路线距离
    [tar(le), len(le)] = funcp(cp,n);
    %温度不断下降
    T =T*K;
    for i = 1:n-1
        plot([cp(i).x, cp(i+1).x], [cp(i).y, cp(i+1).y], "o-","LineWidth", 1.2);
        hold on;
        grid on;
    end
    plot([cp(n).x, cp(1).x], [cp(n).y, cp(1).y],'r-.',"LineWidth", 1.5);
    for k = 1:n
        text(data(k,1)+0.5,data(k,2)+0.75,num2str(var(k)),'fontsize',10);
    end
    title(['优化最短距离：', num2str(len(le))]);
    disp(['优化最短距离：', num2str(len(le))])
    disp(['起点坐标：', num2str([cp(1).x, cp(1).y])])
    disp(['最后一个站点坐标：', num2str([cp(n).x, cp(n).y])])
    hold off;
    pause(0.001);
end
figure(2);
plot(tar, 'LineWidth', 1.1)
grid on;
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进行曲线')
disp('优化结束')
%% ------------------------------------------------------------------------
%计算目标函数和路线总长度函数
function [tar, len] = funcp(cp,n)
tar = 0;
len = 0;
for i = 1:n-1
    tar = tar+sqrt((cp(i).x-cp(i+1).x)^2+(cp(i).y-cp(i+1).y)^2)+10*(1000-var(i)); 
    len = len+sqrt((cp(i).x-cp(i+1).x)^2+(cp(i).y-cp(i+1).y)^2);
end
tar = tar+sqrt((cp(n).x-cp(1).x)^2+(cp(n).y-cp(1).y)^2)+10*(1000-var(1));
len = len+sqrt((cp(n).x-cp(1).x)^2+(cp(n).y-cp(1).y)^2);
end

最优解之一：

Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题
查看路线的起点和终点（最后一个配送站点）：

>> disp(['起点坐标：', num2str([cp(1).x, cp(1).y])])
起点坐标：18  28
>> disp(['最后一个站点坐标：', num2str([cp(n).x, cp(n).y])])
最后一个站点坐标：21  30

可在data_all.mat的第一列数据中看到各坐标点对应的节点标号。

适应度进行曲线：

Baltamatica 北太天元 —— 基于模拟退火算法的旅行商问题

baltam 代码：

clc;
clear;
clf;
%% ------------------------------------------------------------------------
%加载数据
cp_x = load('cp_x.mat');
cp_y = load('cp_y.mat');
vars = load('var.mat');
data = zeros(25,2);
%% ------------------------------------------------------------------------
%模拟退火参数设置
n = size(data,1);  %站点数量
indx = 1:n;
T = 100*n;         %初始温度
L = 100;           %马尔可夫链长度
K = 0.99;          %衰减参数
%% ------------------------------------------------------------------------
%站点坐标结构体
varm = vars.var;
cp = struct('x',cp_x.cp_x,'y',cp_y.cp_y);
cpx = cp.x;
cpy = cp.y;
xx = cp.x;
yy = cp.y;
lem = 1;            %迭代次数
[tar(lem), len(lem)] = funcp(cpx,cpy,n,varm);
figure('Color','white');
while T > 0.001    %停止迭代温度
    %多次迭代扰动，温度降低前多次实验
    for cnt = 1:L
        %计算原路线距离
        [tar1, ~] = funcp(cpx,cpy,n,varm);
        %产生随机扰动
        %随机置换两个不同站点的坐标
        p1 = floor(1+n*rand());
        p2 = floor(1+n*rand());
        while p1 == p2
            p1 = floor(1+n*rand());
            p2 = floor(1+n*rand());
        end
        tmp_cpx = cpx;
        tmpx = tmp_cpx(p1);
        tmp_cpx(p1) = tmp_cpx(p2);
        tmp_cpx(p2) = tmpx;
        tmp_cpy = cpy;
        tmpy = tmp_cpy(p1);
        tmp_cpy(p1) = tmp_cpy(p2);
        tmp_cpy(p2) = tmpy;
        %% ----------------------------------------------------------------
        %计算新路线总距离
        [tar2, ~] = funcp(tmp_cpx,tmp_cpy,n,varm);
        %% ----------------------------------------------------------------
        %新老距离的差值，相当于能量
        delta_e = tar2-tar1;
        %% ----------------------------------------------------------------
        %若新路线好于旧路线，用新路线代替旧路线
        if delta_e < 0
            cpx = tmp_cpx;
            cpy = tmp_cpy;
        else
            %依概率选择是否接收新解
            if exp(-delta_e/T) > rand()
                cpx = tmp_cpx;
                cpy = tmp_cpy;
            end
        end
    end
    lem = lem+1;
    %% --------------------------------------------------------------------
    %计算新路线距离
    [tar(lem), len(lem)] = funcp(cpx,cpy,n,varm);
    disp(["优化最短距离：", num2str(len(lem))])
    disp(["起点坐标：", num2str([cpx(1), cpy(1)])])
    disp(["最后一个站点坐标：", num2str([cpx(n), cpy(n)])])
    %温度不断下降
    T =T*K;
    for jj = 1:n-1
        plot([cpx(jj), cpx(jj+1)], [cpy(jj), cpy(jj+1)], "o-","LineWidth", 1.2);
        hold on;
    end
    plot([cpx(n), cpx(1)], [cpy(n), cpy(1)],'r-.',"LineWidth", 1.5);
    axis([0,120,-2,58]);
    for kk = 1:n
        text(xx(kk)+0.5,yy(kk)+0.75,num2str(varm(kk)),'fontsize',10);
        text(xx(kk)+0.5,yy(kk)-0.75,num2str(indx(kk)),'fontsize',8);
    end
    title(['优化最短距离：', num2str(len(lem))]);
    hold off;
end
figure('2');
plot(tar, 'LineWidth', 1.1)
axis([0,length(len),floor(min(len)),ceil(max(len))])
xlabel("迭代次数")
ylabel("目标函数值")
title('适应度进行曲线')
disp("优化结束")
%% ------------------------------------------------------------------------
计算目标函数和路线总长度函数
function [tar, len] = funcp(cpx,cpy,n,varm)
tar = 0;
len = 0;
for ii = 1:n-1
    tar = tar+sqrt((cpx(ii)-cpx(ii+1))^2+(cpy(ii)-cpy(ii+1))^2)+10*(1000-varm(ii)); 
    len = len+sqrt((cpx(ii)-cpx(ii+1))^2+(cpy(ii)-cpy(ii+1))^2);
end
tar = tar+sqrt((cpx(n)-cpx(1))^2+(cpy(n)-cpy(1))^2)+10*(1000-varm(1));
len = len+sqrt((cpx(n)-cpx(1))^2+(cpy(n)-cpy(1))^2);
end