【数据结构】算法题：邻接表构造相应的逆邻接表-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】算法题：邻接表构造相应的逆邻接表。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

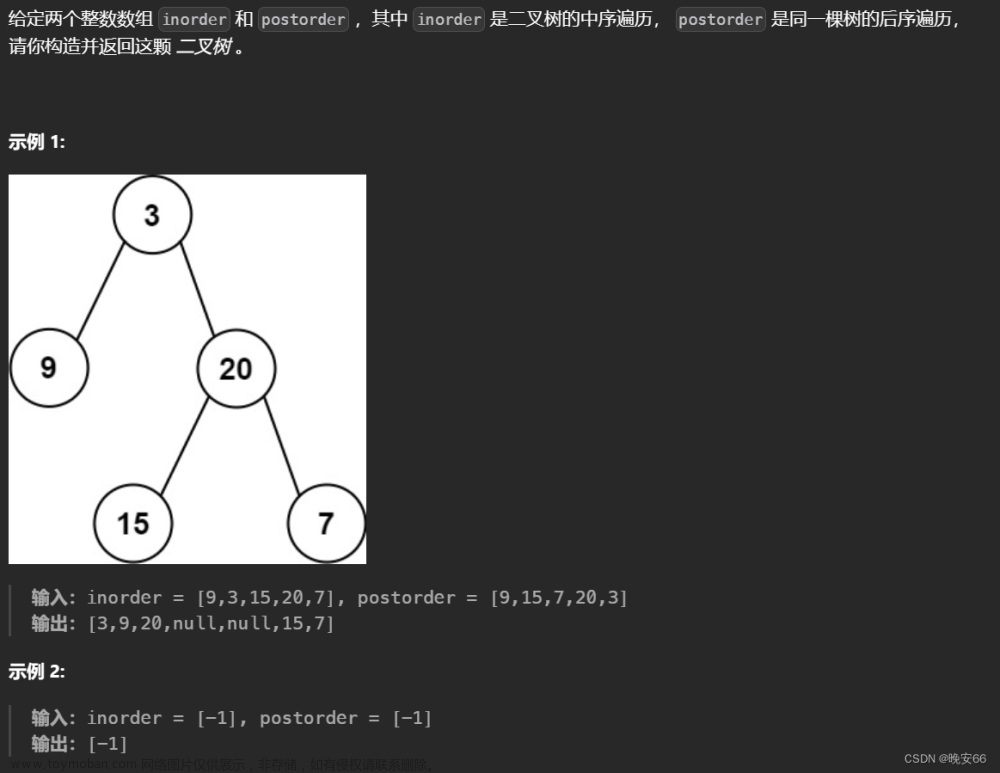
编写算法：根据含有n个顶点的有向图邻接表，构造相应的逆邻接表。

1.算法的思想：
邻接表和逆链接表的顶点信息是相同的，直接复制即可。把出边信息转换成入边信息，则需要逐一访问邻接表的各结点的出边表，把边结点通过头插法插入相应的入边表中。

2.算法的实现：

typedef struct node{		/*边表结点*/	
	int adjvex;				/*邻接点域*/	
	struct node * next;		/*指向下一个邻接点的指针域*/	
}EdgeNode;					/*若要表示边上信息，则应增加一个数据域info*/	

typedef struct ArcNode{
	int adjvex;				//该边所指向的结点的位置	
	ArcNode *nextarc;		//指向下一条边的指针	
}ArcNode;

typedef struct vnode{		/*顶点表结点*/	
	char vertex [20];		/*顶点域*/	
	EdgeNode *firstedge;	/*边表头指针*/	
	ArcNode *firstarc;		//指向第一条边的指针	
}VertexNode;

/*AdjList是邻接表类型*/	
typedef VertexNode AdjList[MaxVerNum];	

typedef struct {
	AdjList adjlist;		/*邻接表*/	
	int n,e;				/*顶点数和边数*/	
}ALGraph;

//将有向图的出度邻接表改为按入度建立的逆邻接表
void InvertAdjList(AdjList ginAdjList gout)
{
	int j;
	ArcNode *s;
	for(i=1;i<=n;i++)	   //设有向图有n个顶点，建逆邻接表的顶点	
	{
		gin[i].vertex==gout[i].vertex;	//邻接表和逆链接表的顶点信息是相同的，直接复制即	
		gin.firstarc=null;	//指向第一条边的指针为空	
	}
	for(i=1;i<=n;i++)	  //邻接表转为逆邻接表	
	{
		p=gout[i].firstarc;	//取指向邻接表的指针	
		while(p!=null){
			j=p->adjvex;	  			//该边所指向的结点的位置	
			s=(rcNode*)malloc(sizeof(ArcNode));	//申请结点空间	
			s->adjvex=i;	   			//把边结点通过头插法 插入到相应的入边表	
			s->next=gin[j].firstarc; gin[j].firstarc=s;
			p=p->next;					//下一个邻接点	
		}
	}
}

举个栗子：
【数据结构】算法题：邻接表构造相应的逆邻接表
邻接表：

逆邻接表：

注：
一个稀疏图顶点个数为n，边数为e。为了解决在存储稀疏图邻接矩阵（使用存储空间 n² ）浪费空间的这一劣势，引入邻接表（ n+2e）来减少存储空间的浪费。
邻接表虽然在空间上有很大的优势，但是对于有向图来说，若需查找入度的个数就需要遍历整个邻接表，所以也不方便，效率有点低哦，解决这个问题有两种方法：
1：十字交叉链表
2：逆邻接表（与邻接表共同使用，达到更好的效果）文章来源地址https://www.toymoban.com/news/detail-508679.html