支持向量机(support vector machine,SVM)是一种新的机器学习方法，其基础是Vapnik 创建的统计学习理论(statistical learning theory,STL)。统计学习理论采用结构风险最小化(structural risk minimization,SRM)准则，在最小化样本点误差的同时，最小化结构风险，提高了模型的泛化能力，且没有数据维数的限制。在进行线性分类时，将分类面取在离两类样本距离较大的地方；进行非线性分类时通过高维空间变换，将非线性分类变成高维空间的线性分类问题。
本章将详细介绍支持向量机的分类原理，并将其应用于基于乳腺组织电阻抗频谱特性的乳腺癌诊断。
1 理论基础
1.1 支持向量机分类原理
1.线性可分SVM
支持向量机最初是研究线性可分问题而提出的，因此，这里先详细介绍线性SVM的基本思想及原理。
值得一提的是，若数据集中的绝大多数样本是线性可分的，仅有少数几个样本(可能是异常点)导致寻找不到最优分类超平面。针对此类情况，通用的做法是引入松弛变量，并对式(28-7)中的优化目标及约束项进行修正，即
2.线性不可分SVM
在实际应用中，绝大多数问题都是非线性的，这时对于线性可分SVM是无能为力的。对于此类线性不可分问题，常用的方法是通过非线性映射φ:R?→H,将原输入空间的样本映射到高维的特征空间H中，再在高维特征空间H中构造最优分类超平面，如图28-2所示。另外，与线性可分SVM相同，考虑到通过非线性映射到高维特征空间后仍有因少量样本造成的线性不可分情况，亦考虑引入松弛变量。
3.多分类SVM
由线性可分SVM和线性不可分SVM的原理可知，支持向量机仅限于处理二分类问题，对于多分类问题，须做进一步的改进。目前，构造多分类SVM的方法主要有两个：直接法和间接法。直接法通过修改待求解的优化问题，直接计算出用于多分类的分类函数，该方法计算量较大、求解过程复杂、花费时间较长，实现起来比较困难。间接法主要是通过组合多个二分类SVM来实现多分类SVM的构建，常见的方法有一对一(one-against-one)和一对多(one-against-all)两种，
1.2 libsvm软件包简介
libsvm工具箱是台湾大学林智仁(C.JLin)等人开发的一套简单的、易于使用的SVM模式识别与回归机软件包，该软件包利用收敛性证明的成果改进算法，取得了很好的结果。libsvm共实现了5种类型的SVM:C-SVC,u-SVC,One Class-SVC,e-SVR和v-SVR等。下面将详细介绍libsvm软件包中主要函数的调用格式及注意事项。
1.SVM训练函数svmtrain
函数svmtrain用于创建一个SVM模型，其调用格式为
model= svmtrain(train_label,train_matrix,'libsvm_options');
其中，train_label为训练集样本对应的类别标签；train_matrix为训练集样本的输入矩阵；libsvm_options为SVM模型的参数及其取值(具体的参数、意义及其取值请参考libsvm软件包的参数说明文档，此处不再赘述);model为训练好的SVM模型。值得一提的是，与BP神经网络及RBF神经网络不同，train_label及train_matrix为列向量(矩阵),每行对应一个训练样本。
2.SVM预测函数svmpredict
函数svmpredict用于利用已建立的SVM模型进行仿真预测，其调用格式为
[predict _label,accuracy]= svmpredict(test_label,test _matrix,model);
其中，test_label为测试集样本对应的类别标签；test_matrix为测试集样本的输入矩阵；model为利用函数svmtrain训练好的SVM模型；predict_label为预测得到的测试集样本的类别标签；accuracy为测试集的分类正确率。需要说明的是，若测试集样本对应的类别标签test_label未知，为了符合函数svmpredict调用格式的要求，随机填写即可，在这种情况下，accuracy便没有具体的意义了，只需关注预测的类别标签predict_label即可。
2 案例背景
2.1 问题描述
乳腺是女性身体的重要器官，乳腺疾病类别繁多，病因复杂，其中，乳腺癌是乳腺疾病的一 种，逐渐成为危害女性健康的主要恶性肿瘤之一。近年来，乳腺癌等乳腺疾病发病率呈明显上升趋势，被医学界称为“女性健康第一杀手”。
相关研究结果表明，在直流状态下，不同生物组织表现出不同的电阻特性，生物组织电阻抗随着外加电信号频率的不同而表现出较大的差异。常见的电阻抗测量方法有：电阻抗频谱法(impedance spectroscopy)、阻抗扫描成像法(electrical impedance scanning,EIS)、电阻抗断层成像法(electrical impedance tomography,EIT)等。电阻抗频谱法的测量依据是生物组织的电阻抗随着外加电信号频率的不同而呈现出较大的差异。阻抗扫描成像法的原理是癌变组织与正常组织及良性肿瘤组织的电导(阻)率相比，存在着显著性的差异，从而使得均匀分布在组织外的外加电流或电压场产生畸变。电阻抗断层成像法则利用设于体表外周的电极阵列及微弱测量电流，提取相关特征并重新构造出截面的电阻抗特性图像。
尽管目前的电阻抗测量结果还存在一些偏差，但相关研究已经证实癌变组织与正常组织的电阻抗特性存在显著的差异。因此，乳腺组织的电阻抗特征可以应用于乳腺癌的检查与诊断中。由于电阻抗测量法具有无创、廉价、操作简单、医生与病人易于接受等优点，随着测量技术的不断发展，电阻抗测量系统精度的日益提高，基于乳腺组织电阻抗特性的乳腺癌诊断技术势必会在临床检查与诊断中发挥其特有的作用。
1996年，Jossinet研究小组利用电阻抗频谱法测量了来自64位妇女的106个乳腺样本的电阻抗特性，并将其分为6组：乳腺组织、结缔组织、脂肪组织、乳腺病、纤维腺瘤和乳腺癌，其中前3组是正常组织，后3组是病变组织(其中前2组是良性病变)。各组的乳腺样本数如表28-1所列。
2.2 解题思路及步骤
依据问题描述中的要求，利用SVM建立乳腺癌诊断模型并对模型的性能进行评价，大体上可以分为以下几个步骤，如图28-5所示。
1.产生训练集/测试集
与前面几章类似，要求所产生的训练集样本数不宜太少，且应具有代表性。同时，由于libsvm软件包对输入的数据有格式上的要求，需要转换产生的训练集和测试集输入矩阵和类别标签以满足函数svmtrain和函数svmpredict调用格式的要求。
2.创建/训练SVM诊断模型
利用函数svmtrain可以方便地创建/训练一个SVM模型，值得一提的是，在创建之前，如若需要，还应对数据进行归一化。同时，由于不同核函数类型及参数对模型的泛化能力影响较大，因此，需要确定核函数类型及选择较好的参数。一般选用RBF核函数，且利用交叉验证方法选择较好的模型参数。
3.仿真测试
当SVM诊断模型训练好后，输入测试集的类别标签及输入矩阵函数svmpredict,便可以得到对应的预测类别标签及正确率。
4.性能评价
依据函数svmpredict返回的正确率，可以对建立的模型性能进行评价。若模型性能不理想，可以从以下3个方面进行调整：训练集的选择、核函数的选择及模型参数的取值，并在此基础上重新建立模型，直到模型的性能达到要求为止。
3 MATLAB程序实现
利用MATLAB及libsvm软件包中提供的函数，可以方便地在MATLAB环境下实现上述步骤。
%% 清空环境变量
clear all
clc
%% 导入数据
load BreastTissue_data.mat
% 随机产生训练集和测试集
n = randperm(size(matrix,1));
% 训练集——80个样本
train_matrix = matrix(n(1:80),:);
train_label = label(n(1:80),:);
% 测试集——26个样本
test_matrix = matrix(n(81:end),:);
test_label = label(n(81:end),:);
%% 数据归一化
[Train_matrix,PS] = mapminmax(train_matrix');
Train_matrix = Train_matrix';
Test_matrix = mapminmax('apply',test_matrix',PS);
Test_matrix = Test_matrix';
%% SVM创建/训练(RBF核函数)
% 寻找最佳c/g参数——交叉验证方法
[c,g] = meshgrid(-10:0.2:10,-10:0.2:10);
[m,n] = size(c);
cg = zeros(m,n);
eps = 10^(-4);
v = 5;
bestc = 1;
bestg = 0.1;
bestacc = 0;
for i = 1:m
for j = 1:n
cmd = ['-v ',num2str(v),' -t 2',' -c ',num2str(2^c(i,j)),' -g ',num2str(2^g(i,j))];
cg(i,j) = svmtrain(train_label,Train_matrix,cmd);
if cg(i,j) > bestacc
bestacc = cg(i,j);
bestc = 2^c(i,j);
bestg = 2^g(i,j);
end
if abs( cg(i,j)-bestacc )<=eps && bestc > 2^c(i,j)
bestacc = cg(i,j);
bestc = 2^c(i,j);
bestg = 2^g(i,j);
end
end
end
cmd = [' -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg)];
% 创建/训练SVM模型
model = svmtrain(train_label,Train_matrix,cmd);
%% SVM仿真测试
[predict_label_1,accuracy_1] = svmpredict(train_label,Train_matrix,model);
[predict_label_2,accuracy_2] = svmpredict(test_label,Test_matrix,model);
result_1 = [train_label predict_label_1];
result_2 = [test_label predict_label_2];
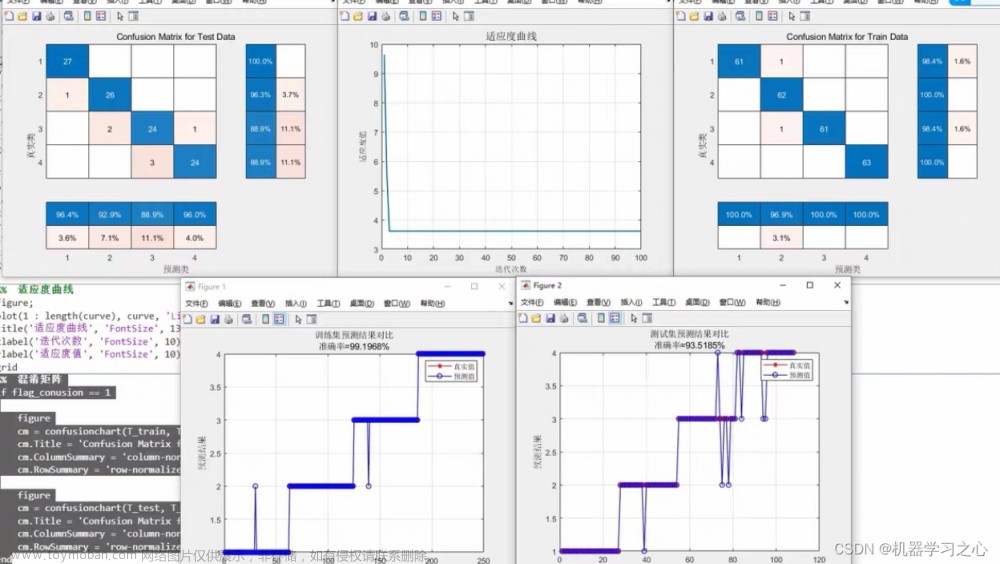
%% 绘图
figure
plot(1:length(test_label),test_label,'r-*')
hold on
plot(1:length(test_label),predict_label_2,'b:o')
grid on
legend('真实类别','预测类别')
xlabel('测试集样本编号')
ylabel('测试集样本类别')
string = {'测试集SVM预测结果对比(RBF核函数)';
['accuracy = ' num2str(accuracy_2(1)) '%']};
title(string)PS:如果提示：错误使用 svmtrain (line xxx) Y must be a vector or a character array.说明你的matlab中已经不包含libsvm工具箱以及svmtrain函数，改用fitcsvm即可。
由于训练集和测试集是随机产生的，所以程序每次运行的结果都会不同。某次运行的测试集预测结果如表28-3所列。从表中可以清晰地看到，只有样本7和9预测错误，测试集的预测正确率达到92.31%(24/26)。且如前文所述，乳腺癌、纤维腺瘤和乳腺病(标签分别为1、2和3)为病变组织，乳腺组织、结缔组织和脂肪组织(标签分别为4、5、6)为正常组织，若仅判断为病变组织或正常组织(即二分类),则样本9则判断正确(将乳腺癌诊断为纤维腺瘤，同为病变组织),预测正确率将达到96.15%(25/26),这也从另外一个角度体现了SVM用于二分类的优越性。
4 延伸阅读
4.1 性能对比
1.归一化对模型性能的影响
为了评价归一化对模型性能的影响，这里尝试不对输入矩阵进行归一化，测试集的预测结果如表28-4所列。从表中可以看出，相比于归一化情况，未归一化的测试集预测正确率要低很多，仅为23.08%(6/26)。然而，需要说明的是，归一化并非一个不可或缺的处理步骤，针对具体问题应进行具体分析，从而决定是否要进行归一化。
文章来源：https://www.toymoban.com/news/detail-509146.html
2.核函数对模型性能的影响
保证其他模型参数不变，仅修改核函数的类型，选择不同核函数时的训练集及测试集预测正确率如表28-5所列。从表中可以清晰地看到，线性核函数和Sigmoid核函数对应的正确率较低，而RBF核函数和多项式核函数对应的训练集预测正确率相当，但从模型的泛化能力考虑，即同时衡量测试集的预测正确率，则RBF核函数对应的模型性能最佳。因此，如前文所述，一般采用默认设置的RBF核函数进行建模。
文章来源地址https://www.toymoban.com/news/detail-509146.html
4.2 案例延伸
近年来，越来越多的专家与学者致力于SVM方面的研究，取得了许多进展。一方面，针对目前的SVM训练算法复杂度较大、计算时间较长等问题，不少学者提出了新的训练算法；另一方面，一些专家尝试着寻找更简单、更有效的核函数以简化运算并提升SVM的性能。同时，为了解决模型参数大多依靠经验选取或者大范围网格搜索耗时较长等问题，不少学者引入遗传算法、粒子群算法等优化算法，从而自动寻找最佳的模型参数使得模型的性能达到最优。
到了这里，关于(转载)支持向量机(support vector machine, SVM)的分类(matlab实现)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
