多状态动态规划之删除并获得点数-Toy模板网

这篇具有很好参考价值的文章主要介绍了多状态动态规划之删除并获得点数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 题目分析

题目链接选自力扣 : 删除并获得点数

结合示例 1 来分析 : 由于它不是有序的, 对于我们理解实例有点不太方便, 因此我们将示例 1 排序后在来看

也就是说, 选择那个节点删除后就获得这个值对应节点数. 同时这个节点的值相邻的值不能选

2. 状态表示

这时候用用动态规划来解还是一头雾水中, 怎么就能和动态规划联系上了呢 ?

先来看这样一组示例 : 1 2 3 4 5

当我们把 1 选上后, 相邻值的 2 就要被删掉. 因此它下一个位置只能在 3 开始往后, 例如下面这样

这时候这个问题就变成了当选中 1 以后, 相邻的不能选, 选择后面 3 ~ 5 位置的最大节点数加上 1 位置的节点数.即为最终的最大节点数.

这时候惊人的发现, 有没有很像我们的 " 打家劫舍(详细链接) " 问题 ? 相邻两个数不能偷窃, 从任意一个位置开始到结束时的最大偷窃金额.

虽然它非常接近我们的 " 打家劫舍 " , 但是此处我们的数组之间的数值不一定是连续的. 例如 : 1 1 2 2 4 4 6

此时在带入到 " 打家劫舍(详细链接) " 问题时就不合适了. 偷了 1 位置则不能偷 2 位置, 可以从 3 位置开始偷, 但这不符合我们题目的要求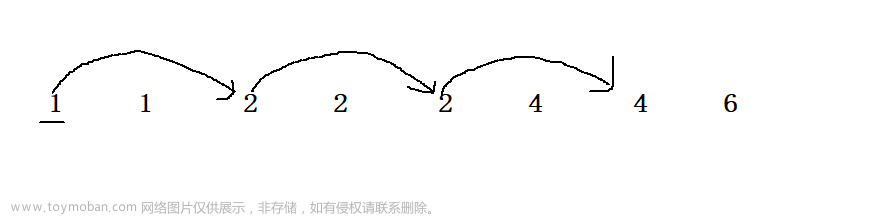

这是按照 " 打家劫舍(详细链接) " 问题的思路来偷窃的. 显然是不行的, 因为题目要求选了 1 以后, 相邻数值的节点数 2 和 0 都要被删除, 应该为这样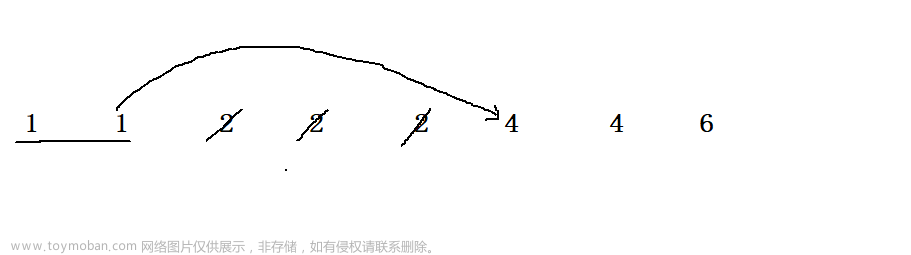

因此, 为了解决这种情况, 我们需要将这个数组给它进行预处理, 让它变成可以使用 " 打家劫舍(详细链接) " 问题来解决的数组形式, 即:利用下标连续来对应 " 打家劫舍 " 问题的连续数组 !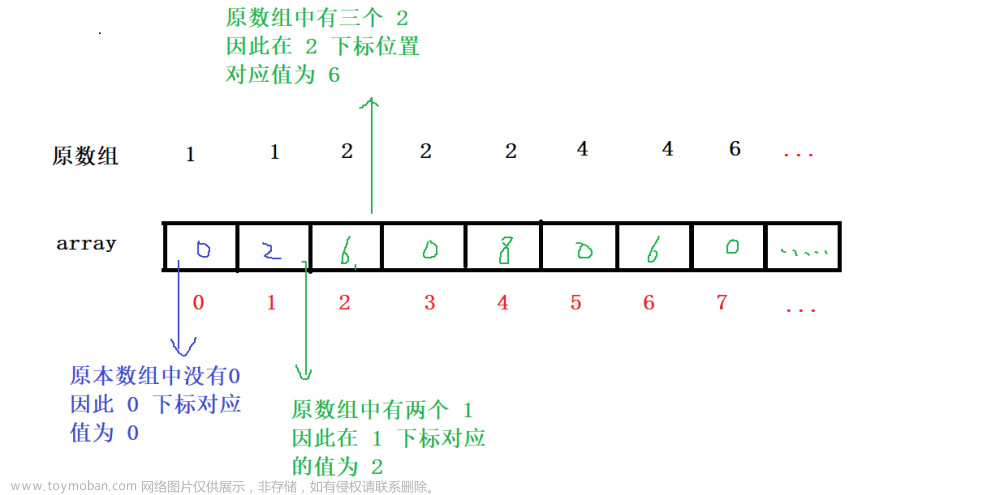

创建一个数组来存储统计原数组中的相同的值. 0 下标处就统计原数组中有多少个 0, 1 下标处就统计原数组中有多少个 1, 2 下标处就统计原数组中有多少个 2 … 以此类推. 最终根据下标的连续性来进行 " 打家劫舍(详细链接) " 问题的处理.
处理后的数组我们来演示一下 :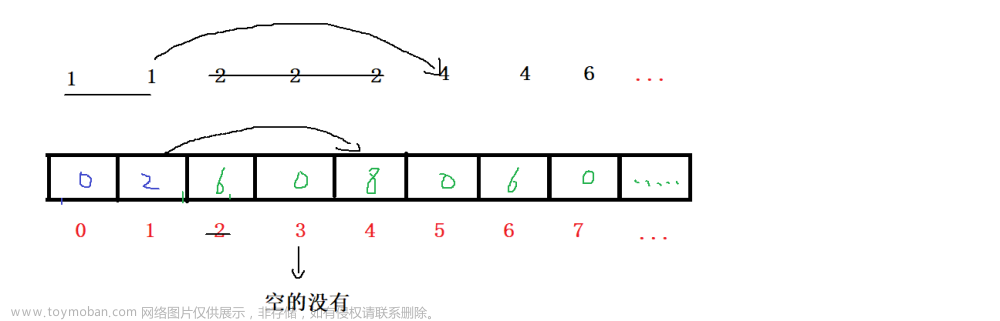
当选择所有 1 节点数后, 所有的节点值为 0 和 2 的都要被删除. 此时选择两个 1 节点获得 2 点节点数. 下一次只能选从 4 位置开始.

在看我们的处理后的数组. 偷窃 1 号房间后, 2 号房间就不能偷了, 那么只能从 3 号房间开始偷. 但是 3 号房间不存在. 因此只能从 4 号房间开始偷. 最终的最多盗窃金额就为 nums[1] + [4-n-1] 区间内的最多盗窃金额. 就可以对应上我们的 " 打家劫舍(详细链接) " 问题了.

3. 状态转移方程

既然是一个 " 打家劫舍 " 问题. 那么就来回顾一下它的状态转移方程. 下面的盗窃金额即为题目的最大节点数 !

以 i 位置为结尾, 从任意位置开始偷窃到 i 位置时的最大盗窃金额. 即 dp[i]. 偷窃到 i 位置时, 我们还可以细分为两个状态, 也就是偷窃 i 位置的 array[i] 和不偷窃 i 位置的 array[i]

偷窃到 i 位置时, 偷窃 array[i]

这种情况我们表示为 f[i]. 即从某一位置开始偷窃到 i 位置时, 并偷窃 array[i]

偷窃到 i 位置时, 不偷窃 array[i]

这种情况我们表示为 g[i]. 即从某一个位置开始偷窃到 i 位置时, 不偷窃 array[i]

来推导一下这两种情况下的状态转移方程.

偷窃到 i 位置时, 偷窃 array[i]

偷窃到 i 位置后, 选择偷窃 array[i], 那么此时 i - 1 位置是必定不能偷的. 因此最大的偷窃金额就为从任意位置起始到 i - 1 位置并且 array[i-1] 位置不偷窃. 对应到我们的状态表示则为 g[i-1], 最后在加上必偷的 array[i].

最终最大的偷窃金额为, 即状态转移方程:f[i] = g[i-1] + array[i]

偷窃到 i 位置时, 不偷窃 array[i]

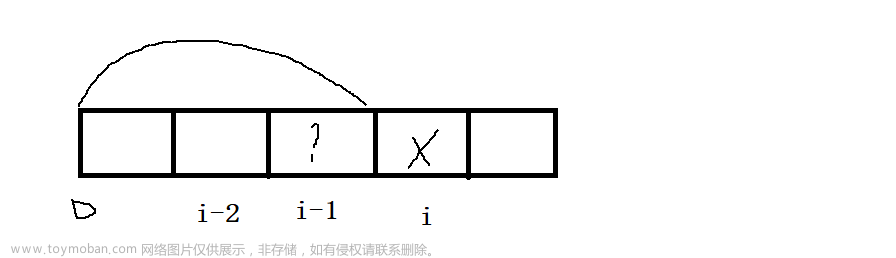
这种情况下, 偷窃到 i 位置时, array[i] 不偷窃, 那么 i - 1 位置就有两种情况可以选

i-1 位置偷窃 array[i-1]

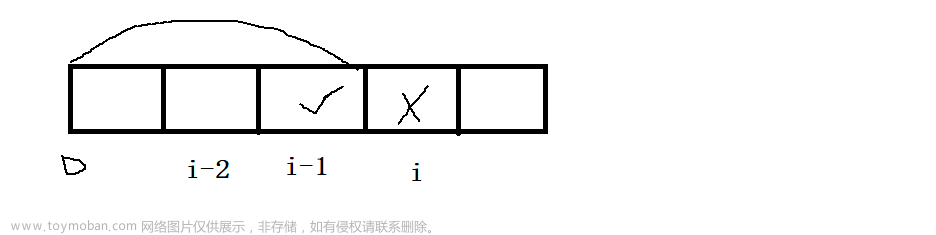
这个情况下, 也就是从起始位置偷窃到 i - 1 位置, 并且偷窃 array[i-1] 正好对应到我们的状态表示中的 f[i-1]. 最大的盗窃金额即为 f[i-1]

i-1 位置不偷窃 array[i-1]

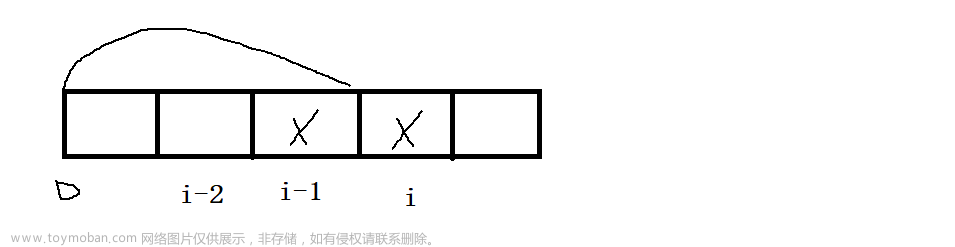
偷窃到 i -1 位置时, 不偷窃 array[i-1], 正好对应我们的状态表示中的 g[i-1]. 最大盗窃金额即为 f[i-1]

第二种情况的状态转移方程是有两种细分的情况组成的. 最终这种情况下的最大偷窃金额为两种情况的最大值, 即状态转移方程 : g[i] = Math.max(f[i-1], g[i-1])

4. 初始化

根据两种不同转态的状态转移方程 f[i] = g[i-1] + array[i] 和 g[i] = Math.max(f[i-1], g[i-1]) 知道, 填写 g[0] 和 f[0] 时会发生越界错误. 因此这两个位置需要进行初始化.

经过分析, 当只有一个元素时, 此时有两种偷窃情况.

偷窃这个位置的 array[0], 最终的偷窃金额为 f[0] = array[0]
不偷窃这个位置的 array[0], 最终的偷窃金额为 g[0] = 0

5. 填表顺序

根据状态转移方程, 想要填写 i 位置的值, 就必须先知道前一个位置的值. 因此填表的顺序为从左往右

6. 返回值

题目要求从某一位置开始到数组末尾 n-1 位置结束时存储的最大盗窃金额. 由于存在两种状态, 因此对这两种状态的结尾值取最大值返回. Math.max(f[n-1], g[n-1])文章来源地址https://www.toymoban.com/news/detail-509360.html

7. 代码演示

class Solution {
    public int deleteAndEarn(int[] nums) {

        // 1. 创建 dp 表
        int n = 10001; // 和预处理的数组一样大, 下标直接对应不需要考虑映射关系

        int[] f = new int[n]; // 从任意位置删除到 i 位置时, 选择 nums[i]时所获得的最大节点数
        int[] g = new int[n]; // 从任意位置删除到 i 位置时, 不选择 nums[i]所获得的最大节点数
        
        // 预处理 nums 数组让其下标连续对应 "打家劫舍" 问题
        int[] array = new int[n]; // 根据题目开辟足够大的空间存储
        for(int x : nums) {
            array[x] += x; 
        }

        // 2. 初始化
        f[0] = array[0];

        // 3. 填写 dp 表
        for(int i = 1; i < n; i++) {
            // 根据不同的状态转移方程填写
            f[i] =  g[i-1] + array[i];
            g[i] = Math.max(f[i-1], g[i-1]);
        }

        // 4. 确认返回值
        return Math.max(f[n-1], g[n-1]);
    }
}