稀疏矩阵的运算-加、减、乘、转置(C-数据结构)-Toy模板网

这篇具有很好参考价值的文章主要介绍了稀疏矩阵的运算-加、减、乘、转置(C-数据结构)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

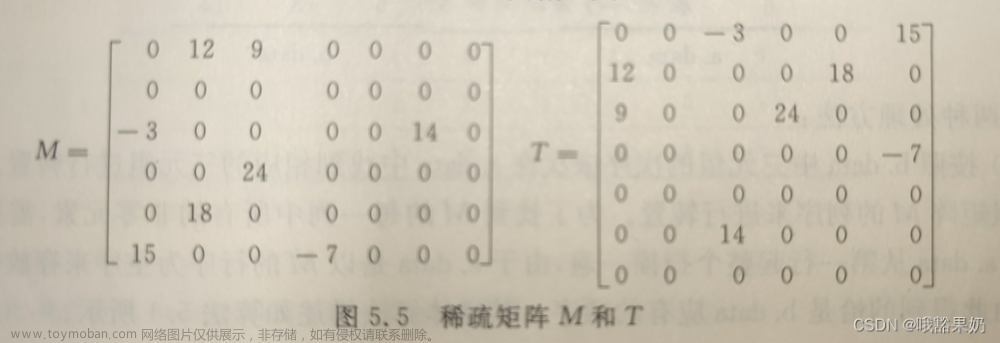
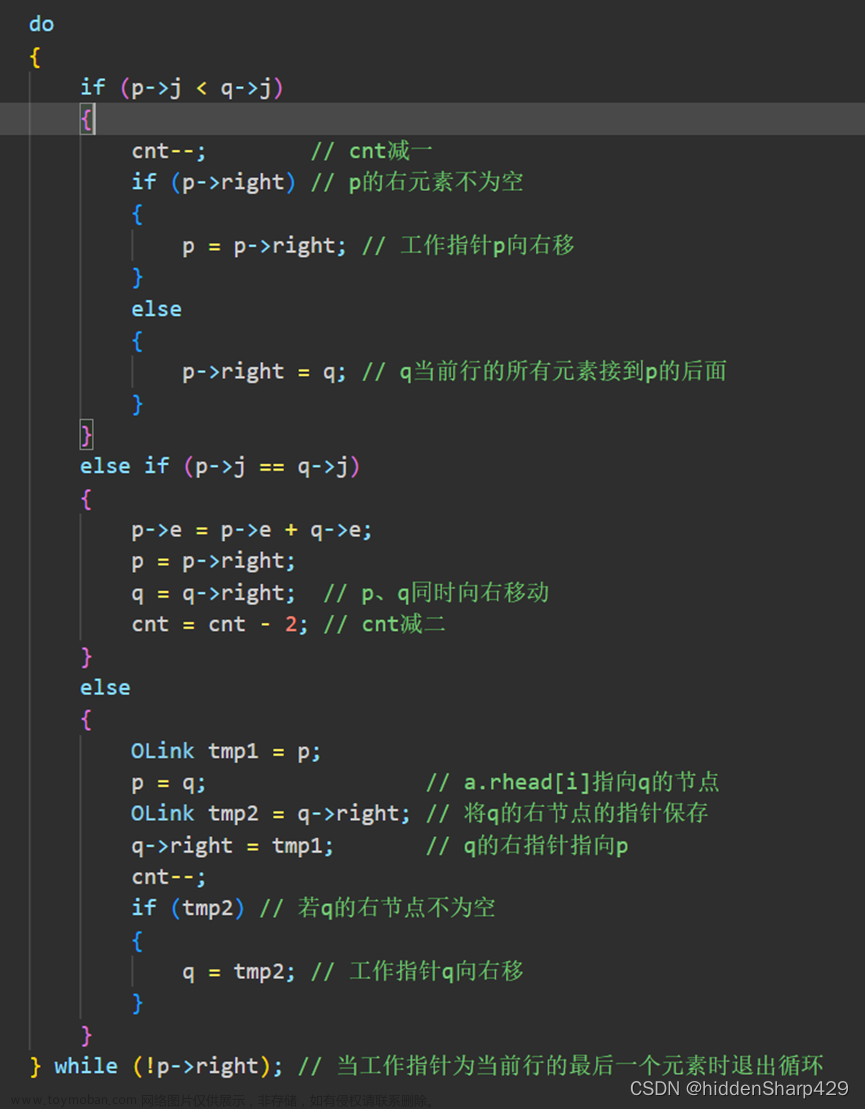
题目

以三元组的形式给出输入数据，选择对应的运算后给出对应输出结果(稀疏矩阵的运算器)

思路

页面布局就不说了，这里大概说一下各个运算模块的实现
加减法
将三元组中对应的元素行列位置进行比较，将较为靠前的元素直接放进新的三元组存储结构，位置相同的元素通过对应符号判断是加法还是减法，运算后放入新的三元组存储结构，最后输出即可，具体结合代码
乘法
根据输入的两个矩阵，对结果矩阵的行数和列数进行初始化，然后分别求结果矩阵的每一个元素，如果为非零元素，将其加入三元组存储结构，具体结合代码
转置
使用num1数组记录每一列的元素数量，用pos数组记录结果矩阵中每一行的第一个非零元素的位置，然后遍历需要计算的矩阵的非零元素，放入对应位置即可，每次放入后需要将pos数组中对应位置加一，因为此处已经放元素了，下一次就应该放在下一个位置(所以pos[i]数组实际上表示的是原矩阵对应列为i的元素应该放在结果矩阵中的位置)。具体结合代码。

测试数据

加法
输入

结果
稀疏矩阵的运算-加、减、乘、转置(C-数据结构)

乘法
输入

结果
稀疏矩阵的运算-加、减、乘、转置(C-数据结构)
转置
输入

结果
稀疏矩阵的运算-加、减、乘、转置(C-数据结构) 文章来源地址https://www.toymoban.com/news/detail-510090.html

代码

#include<stdio.h>

#define MAXSIZE 10000

typedef struct {
	int row;
	int col;
	double value;
}Triple;
typedef struct {
	Triple data[MAXSIZE+1];
	int rows,cols,nums; //行数，列数，非零元素个数 
}TSMatrix;

void init(TSMatrix *p,int m,int n); //初始化 
void input(TSMatrix *p,int num); //输入 
void compute(TSMatrix *p1,TSMatrix *p2,TSMatrix *p3,char c); //计算
void mulCompute(TSMatrix *p1,TSMatrix *p2,TSMatrix *p3); //乘法 
double get(TSMatrix *p,int m,int n);//获取三元组p中存储中处于m行n列的元素值 
void transpose(TSMatrix *p,TSMatrix *p3); //稀疏矩阵的转置 

int main()
{
	TSMatrix x1,x2,x3;
	while(1){
		printf("1--加\n2--减\n3-乘\n4--转置\n5--退出\n请输入计算方式：");
		int choice;
		scanf("%d",&choice);
		switch(choice){
			case 1:
				compute(&x1,&x2,&x3,'+');
				break;
			case 2:
				compute(&x1,&x2,&x3,'-');
				break;
			case 3:
				mulCompute(&x1,&x2,&x3); 
				break;
			case 4:
				transpose(&x1,&x3);
		}
		if(choice==5){
			break;
		}
		printf("结果为(三元组形式---行 列 值)：\n");
		for(int i=1;i<=x3.nums;i++){
			printf("%4d %4d %4.0lf\n",x3.data[i].row,x3.data[i].col,x3.data[i].value);
		}
		printf("矩阵形式为：\n");
		int cnt1=1;
		for(int i=1;i<=x3.rows;i++){
			for(int j=1;j<=x3.cols;j++){
				printf("%4.0lf",cnt1<=x3.nums&&i==x3.data[cnt1].row&&j==x3.data[cnt1].col?x3.data[cnt1++].value:0);
			}
			printf("\n");
		}
		
	}
 } 
 //初始化 
void init(TSMatrix *p,int m,int n)
{
	p->rows=m;
	p->cols=n;
	p->nums=0;
}
//输入 
void input(TSMatrix *p,int num)
{
	int cnt=1;
	for(int i=1;i<=num;i++){
		scanf("%d %d %lf",&p->data[cnt].row,&p->data[cnt].col,&p->data[cnt].value);
		p->nums++;
		cnt++;
	} 
} 
//计算
void compute(TSMatrix *p1,TSMatrix *p2,TSMatrix *p3,char c)
{
	int m,n,num; 
	printf("请输入要进行计算的稀疏矩阵的行数和列数 m n：");
	scanf("%d %d",&m,&n); 
	init(p1,m,n);
	init(p2,m,n);
	init(p3,m,n);	
	printf("请输入第一个矩阵的非零元素个数：\n"); 
	scanf("%d",&num);
	printf("请输入第一个矩阵的非零元素三元组：\n"); 
	input(p1,num);
	printf("请输入第二个矩阵的非零元素个数：\n"); 
	scanf("%d",&num);
	printf("请输入第二个矩阵的非零元素三元组：\n"); 
	input(p2,num);
	int cnt=1;
	int i=1,j=1;
	while(i<=p1->nums&&j<=p2->nums){
		if(p1->data[i].row<p2->data[j].row){
			p3->data[cnt]=p1->data[i];
			p3->nums++;
			cnt++;
			i++;	
		}else if(p1->data[i].row>p2->data[j].row){
			p3->data[cnt]=p2->data[j];
			p3->nums++;
			cnt++;
			j++;
		}else{
			if(p1->data[i].col<p2->data[j].col){
				p3->data[cnt]=p1->data[i];
				p3->nums++;
				cnt++;
				i++;
			}else if(p1->data[i].col<p2->data[j].col){
				p3->data[cnt]=p2->data[j];
				p3->nums++;
				cnt++;
				j++;
			}else{
				p3->data[cnt]=p1->data[i];
				p3->data[cnt].value= c=='+'?p1->data[i].value+p2->data[j].value:p1->data[i].value-p2->data[j].value;
				p3->nums++;
				cnt++;
				i++;
				j++;
			}
		}
	}
	while(i<=p1->nums) {
		p3->data[cnt]=p1->data[i];
		p3->nums++;
		cnt++;
		i++;
	}
	while(j<=p2->nums){
		p3->data[cnt]=p2->data[j];
		p3->nums++;
		cnt++;
		j++;
	}
}
//乘法 
void mulCompute(TSMatrix *p1,TSMatrix *p2,TSMatrix *p3)
{
	int m,n,num,cnt=1;
	printf("请输入第一个稀疏矩阵的行数和列数 m n：");
	scanf("%d %d",&m,&n);
	init(p1,m,n);
	printf("请输入第二个稀疏矩阵的行数和列数 m n：");
	scanf("%d %d",&m,&n);
	init(p2,m,n);
	if(p1->cols!=p2->rows){
		printf("无法进行乘法运算");
		return; 
	}
	init(p3,p1->rows,p2->cols);
	printf("请输入第一个矩阵的非零元素个数：\n"); 
	scanf("%d",&num);
	printf("请输入第一个矩阵的非零元素三元组：\n"); 
	input(p1,num);
	printf("请输入第二个矩阵的非零元素个数：\n"); 
	scanf("%d",&num);
	printf("请输入第二个矩阵的非零元素三元组：\n"); 
	input(p2,num);
	for(int i=1;i<=p1->rows;i++){
		for(int j=1;j<=p2->cols;j++){
			double sum=0;
			//sum表示p1中第i行元素与p2中第j列元素对应相乘之和 
			for(int k=1;k<=p1->cols;k++){
				sum+=get(p1,i,k)*get(p2,k,j); 
			}
			if(sum){
				p3->data[cnt].row=i;
				p3->data[cnt].col=j;
				p3->data[cnt].value=sum;
				cnt++;
				p3->nums++;
			}
		}
	} 
}
//获取三元组p中存储中处于m行n列的元素值
double get(TSMatrix *p,int m,int n)
{
	for(int i=0;i<=p->nums;i++){
		if(p->data[i].row==m&&p->data[i].col==n){
			return p->data[i].value;
		}
	}
	return 0;
}
//稀疏矩阵的转置 
void transpose(TSMatrix *p,TSMatrix *p3)
{
	int m,n,num;
	printf("请输入要进行转置的稀疏矩阵的行数和列数 m n：");
	scanf("%d %d",&m,&n);
	init(p,m,n); 
	printf("请输入该矩阵的非零元素个数：\n"); 
	scanf("%d",&num);
	printf("请输入该矩阵的非零元素三元组：\n"); 
	input(p,num);
	p3->cols=p->rows;
	p3->rows=p->cols;
	p3->nums=p->nums;
	int num1[(p->nums)+1]={0};
	int pos[(p->nums)+1]={0};
	if(p->nums){
		for(int i=1;i<=p->nums;i++){
			num1[p->data[i].col]++;
		}
		pos[1]=1;
		for(int i=2;i<=p->nums;i++){
			pos[i]=pos[i-1]+num1[i-1];
		}
		for(int i=1;i<=p->nums;i++){
			p3->data[pos[p->data[i].col]].col=p->data[i].row;
			p3->data[pos[p->data[i].col]].row=p->data[i].col;
			p3->data[pos[p->data[i].col]].value=p->data[i].value;
			pos[p->data[i].col]++;
		}
	}
}

到了这里，关于稀疏矩阵的运算-加、减、乘、转置(C-数据结构)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！