一、最小生成树
我们先解释一下什么是最小生成树。
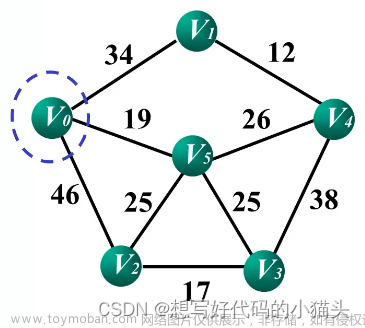
这个概念是基于图的，如果说存在一条路线串通起来了所有的点，那么这条路线就叫做生成树。而在这些路线中最短的那一条就叫做最小生成树。
如上图所示，图中的红色路线就是一个生成树，假设这条红色路线是众多生成树路线中最小的，那么这个路线就叫做最小生成树。而我们后续所讲解的普利姆算法和克鲁斯卡尔算法就是用来解决最小生成树问题的。
二、prim算法
1、算法思路
我们可以将上述图中的点看作两个集合。其中一个集合st是已经确定最小生成树中的边上的点。另外一个集合是还没有确定是否是最小生成树中的边上的点。
我们每次都将未确定的集合dis中，挑选一个距离st集合最近的边对应的点进入集合st。
我每次都选择距离集合最近的边，那么最终得到的就会是最小的生成树。
那么我们如何判断最短的边呢？
其实很简单，就是比较dis集合中点到st集合中的点的距离。距离最近的那个边，自然就是我们想要的边。
那么我们如何判断不存在最小生成树呢？
如果一个不确定的集合内的点，到已经确定的点的集合最短的距离是正无穷。那么就说明此时不存在最小生成树。
那么负环的存在对最小生成树有影响吗？
答案是没有影响，负环之所以会对之前的算法产生影响，是因为我们可以利用负环无限松弛。但是我们现在的prim算法中不需要松弛。我们只在乎边权的大小。
2、算法模板
（1）问题
（2）模板
#include<iostream>
#include<cstring>
using namespace std;
const int N=510;
int g[N][N],dis[N];
bool st[N];
int n,m;
int prim()
{
int ans=0;
memset(dis,0x3f,sizeof dis);
dis[1]=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||dis[t]>dis[j]))t=j;
st[t]=true;
if(dis[t]==0x3f3f3f3f)return 0x3f3f3f3f;
ans+=dis[t];
for(int j=1;j<=n;j++)
if(!st[j]&&dis[j]>g[t][j])dis[j]=g[t][j];
}
return ans;
}
int main()
{
memset(g,0x3f,sizeof g);
cin>>n>>m;
for(int i=0;i<m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(a!=b)
g[a][b]=g[b][a]=min(g[a][b],c);
}
int res=prim();
if(res==0x3f3f3f3f)puts("impossible");
else cout<<res<<endl;
return 0;
}
（3）分析
4、常见疑惑
（1）与dijkstra算法的区别以及循环次数问题：
看完这个思路，我想大家应该会想到我们之前讲解的一个算法：dijkstra算法。这个算法和prim算法是很相似的。都是分成了两个集合。但是不同的是，dijkstra算法中的dis数组是每个点到源点的距离，而prim算法中的dis数组是每个点到集合的距离。
而每个点到源点的距离最多也就经过n-1条边，所以dijkstra算法循环n-1次。
与此同时，最小生成树包含n个点，而我们要判断每个点到集合的距离，所以prim算法需要循环n次。
但两者都采用了相同的思想：贪心思想。
（2）正确性证明：
其实我们的prim算法的核心思想就是dis集合中的点距离st集合内的点最短的边，就是最小生成树路径上的边。
所以我们只需要证明这个观点是正确的。
我们采用反证法的方式去证明：在某次循环中，假设dis数组中存在一个点A其到st集合的点B的距离不是最小的，但是此时的g[a][b]边却是最小生成树的一部分。由于g[a][b]此时不是最小的，那么就必存在一个当前的最小边g[c][d]。如下图所示：
那么我们假设的最小生成树就应该是红色线对应的路径：S+g[a][b]。但是由于g[a][b]>g[c][d]。
所以，S+g[a][b]>S+g[c][d] 。 所以通过AB边构成的最小生成树并不是最小生成树，与刚刚的假设矛盾。
因此，我们的原定理：dis集合中的点距离st集合内的点最短的边，就是最小生成树路径上的边，成立
三、kruskal算法
1、算法用途
我们发现我们刚刚的普利姆算法一般适用于稠密图，因为我们遇到稠密图的时候喜欢用邻接矩阵。
那么假设我们遇到了稀疏图，我们可以选择用prim算法，然后利用优先队列去优化这个算法（和dijkstra算法的优化是一样的），但是这种做法过于麻烦。因此，在这种情况下，我们习惯用的就是相对简单、时间复杂度和优化后的prim算法相同的kruskal算法。
2、算法思想
我们想选择的是最小生成树，也就是说我们想选的是尽可能小的边。好，那么既然这样我不管三七二十一，先将所有的边进行升序排序，然后假设一个st数组，这个数组存储的是最小生成树中的边。接着，我们从小到大遍历所有的边。如果我们遍历的边和当前st数组中的边没有构成环，那么就把这个边放到st数组中，如果构成了环，则说明当前的边不是最小生成树中的边，因此就不把这个边放到st数组中。
3、正确性证明
在开始之前我们需要明确一点：
在排好序的边中，先遍历的边的权重小于后遍历的边的权重。
在明确了这个性质之后，我们先来解决下面的两个问题：
（1）为什么构成环的边不是最小生成树中的边？
我们画出下面的图帮助大家理解：
我们再加入新的边后，某几个点构成了环，这就说明，在新的边加入之前，我们的这几个点已经被连结成了一串联通块。如果一个环，我们删除任意的一条边，也仅仅是将这个环变成线，但这几个点依旧是连通块。同时，最小生成树的边数是n-1，也就是说我们不能存在环。即，我们必须删除环中的任意一条边。由于我们要的是最小生成树，所以我们一定是删除环中最大的边，即我们新加入的边。
同时，我们删除任意一边，都不会影响这一部分和其他连通块的连接。因为，不管我们删除哪一条边，这几个点都是连通的，并且我们的点数也没变，即和外界相连的边都没变。所以，我们删除环上的边，并不影响环上的点和连通块之外的点的连接。也就是说，我们删除新来的成环的边对其余连通块和本连通块之间的连接不会产生任何的影响。
因此，我们新加入的成环的边一定不是答案。
（2）为什么不构成环的边就一定是最小生成树的边？
首先，不构成环也就是说明本条边的加入，连接了两个之前不相连的连通块。那么现在要解决的问题就是，为什么这次加入的连接两个连通块的边就是连接两个连通块的边中最小的。
从我们一开始说的那个规律：**在排好序的边中，先遍历的边的权重小于后遍历的边的权重。**所以如果后面再次出现一个连接两个连通块的边，那么新出现的边也必定是大于我们现在的边的。因此，当我们出现了一个不构成环的边的时候，这个边必定是在最小生成树里的。
4、代码实现思路
好了。通过我们上面的讲解我们已经了解大体的逻辑，同时大概知道了这个算法的正确性。那么我们纵观整体，其实这就是一个集合的合并问题。而集合的合并这个操作可以利用我们之前学过的一个算法—并查集。
如果新遍历的边所对的连通块和遍历之前的连通块的祖先是一样的，这就说明现在我们新遍历的边所在的连通块和我们st数组中的点所在的连通块，就是一个连通块。因此，根据我们刚才的推导，如果我们将已经在一个连通块上的点的新边加进来，就会成环。所以，如果两个连通块的祖先是一样的，则扔掉当前正在遍历的边。
同理，如果我们新加入的边所在的连通块和我们st数组内的边所在的连通块，这二者的祖先是不一样的。说明我们应该加入这个边。所以我们只需要将这个边并入我们的集合，即新边的祖先认爹的过程。
5、模板
（1）问题：
文章来源：https://www.toymoban.com/news/detail-510548.html
（2）代码：
#include<iostream>
#include<algorithm>
using namespace std;
const int N=2e5+10,M=3e5+10;
struct edge
{
int a,b,c;
}edges[N];
int p[N];
int n,m;
int find(int x)
{
if(p[x]!=x)p[x]=find(p[x]);
else return p[x];
}
bool cmp(edge a,edge b)
{
return a.c<b.c;
}
int kruskal()
{
int cnt=0,nums=0;
sort(edges,edges+m,cmp);
for(int i=0;i<m;i++)
{
int pa=find(edges[i].a),pb=find(edges[i].b);
if(pa!=pb)
{
p[pb]=pa;
cnt+=edges[i].c;
nums++;
}
if(nums==n-1)return cnt;
}
return 0x3f3f3f3f;
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
if(x!=y)
edges[i]={x,y,z};
}
for(int i=1;i<=n;i++)
p[i]=i;
int res=kruskal();
if(res!=0x3f3f3f3f)cout<<res<<endl;
else puts("impossible");
return 0;
}
（3）分析：
文章来源地址https://www.toymoban.com/news/detail-510548.html
到了这里，关于第二十一章 Prim算法与Kruskal算法（通俗证明与详细讲解）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
