分支限界法的基本思想
分支限界法的基本思想是,在分支结点上,预先分别估算沿着它的各个儿子结点向下搜索的路径中,目标函数可能取得的“界”,然后把这些儿子结点和它们可能所取得的“界”保存在一张结点表中,再根据题目要求选择表中“界”最大或最小的结点向下搜索。(一般用优先队列来处理这张结点表)这样当搜索到一个叶子结点时,如果该结点所估算的目标函数值就是结点表中的最大或者最小值,那么沿叶子结点到根结点的路径所确定的解就是问题的最优解,叶子结点的目标函数值就是问题的最大值或最小值。
参考:《算法分析与设计(第三版)》(郑宗汉、郑晓明编著)
解决背包问题的基本思路
首先要将物品按重量价值比排序。
同样还是一棵二叉树,沿左孩子则选,右孩子则不选。
初始化最大上界bound = 0。对于一个结点,计算其理想状态下可能获得的最大上界bound(理想状态也就是把物体看成可分割),将结点按bound递减顺序存入优先队列中;然后队头出队(也就是bound最大的结点),对于其左孩子和右孩子分别计算bound,重复上述步骤。如果到达叶子结点,且该叶子结点的bound比当前bound大,则更新bound值。如果队列内的一些结点的值小于bound,则无需沿着小于bound的值的结点继续搜索。(随着二叉树搜索深度增加,bound值越来越接近真实值),那么如果当前结点bound值都比另一条分支上的叶子结点bound值小,那继续搜索只会更小)
源程序代码
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<malloc.h>
#include<Windows.h>
#define N 100
int n;
int M;
typedef struct {
float weight;
float value;
float x;// 价值重量比
int num;//排序前的初始序号
int flag;
}Goods[N];
typedef struct BiTNode {
Goods g;
float bound;//上界
float w;//已选道路重量
float v;
int k;//搜索深度
}BiTNode;
BiTNode* qbase[N];
int choose[N];//物品选择情况
int rear = 0;
int front = 0;//队列指针
//初始化
void Init(Goods goods) {
printf("输入物品数量和背包容量:");
scanf("%d %d", &n, &M);
for (int i = 0; i < n; i++) {
printf("输入第%d个物品的重量和价值:", i + 1);
scanf("%f %f", &goods[i].weight, &goods[i].value);
goods[i].x = goods[i].value / goods[i].weight;
goods[i].num = i;
goods[i].flag = 0;
}
}
//按物品价值重量比递减排序
void sort(Goods goods) {
Goods temp;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - 1 - i; j++) {
if (goods[j].x < goods[j + 1].x) {
temp[0] = goods[j + 1];
goods[j + 1] = goods[j];
goods[j] = temp[0];
}
}
}
}
//入队
void Q_Insert(BiTNode* qbase[], BiTNode* xnode) {
qbase[rear] = xnode;
rear++;
}
//将最大值放在队首
BiTNode* Max_Q(BiTNode* qbase[]) {
float max = 0;
for (int i = front;i < rear;i++) {
if (qbase[i]->bound > max) {
max = qbase[i]->bound;
}
}
for (int i = front;i < rear;i++) {
if (qbase[i]->bound == max) {
BiTNode* xnode = new BiTNode;
xnode = qbase[i];
qbase[i] = qbase[front];
qbase[front] = xnode;
}
}
return qbase[front];
}
//计算结点上界
void knap_bound(BiTNode* node, int M, int n) {
float w = node->w;
float v = node->v;
int m = node->k;
if (node->w > M) {
//已选道路重量如果已经大于背包重量
node->bound = 0;
}
else {
while (m < n && node->w + node->g[m].weight <= M) {
//按实际情况(不可分割)将背包容量尽可能达到最大值
//也就是说加下一个物品超重,但不加则不超重
w += node->g[m].weight;
v += node->g[m].value;
m++;
}
if (m < n) {
//对物品进行分割
//背包剩余容量*物品的价值重量比
//就是该物品一部分(这一部分刚好满足背包装满)的价值
node->bound = v + (M - w) * node->g[m].x;
}
else {
node->bound = v;
}
}
}
//背包问题
float KnapSack(Goods goods) {
BiTNode* xnode, * ynode, * znode;
float bound = 0;
xnode = new BiTNode;
xnode->w = xnode->v = 0;
xnode->k = 0;
for (int i = 0;i < n;i++) {
//将物品信息复制到结点中
xnode->g[i] = goods[i];
}
// ----------------初始化结束-----------------
while (xnode->k < n) {
ynode = new BiTNode;
*ynode = *xnode;
ynode->g[ynode->k].flag = 1;//选
ynode->w += goods[ynode->k].weight;
ynode->v += goods[ynode->k].value;
ynode->k += 1;//搜索深度加一
knap_bound(ynode, M, n);
if (ynode->bound > bound) {
Q_Insert(qbase, ynode);
if (ynode->k == n) {
//叶子结点则更新bound
bound = ynode->bound;
}
}
else {
delete ynode;
}
znode = new BiTNode;
*znode = *xnode;
znode->g[znode->k].flag = 0;//不选
znode->k += 1;
knap_bound(znode, M, n);
if (znode->bound > bound) {
Q_Insert(qbase, znode);
if (znode->k == n) {
bound = znode->bound;
}
}
else {
delete znode;
}
delete xnode;//不要忘记释放结点空间
xnode = Max_Q(qbase);//优先对列中bound最大的结点赋值给xnode
front++;//队头出队,front++
}
float v = xnode->v;//输出最优解
for (int i = 0;i < n;i++) {
if (xnode->g[i].flag != 0) {
//输出最优解向量
choose[xnode->g[i].num] = 1;//num是未排序前的原始序号
}
}
delete xnode;
return v;
}
int main() {
Goods goods;
Init(goods);
sort(goods);
printf("选择物品情况:");
float value = KnapSack(goods);
for (int i = 0;i < n;i++) {
printf("%d ", choose[i]);
}
printf("\n最大价值:");
printf("%.1f", value);
system("pause");
return 0;
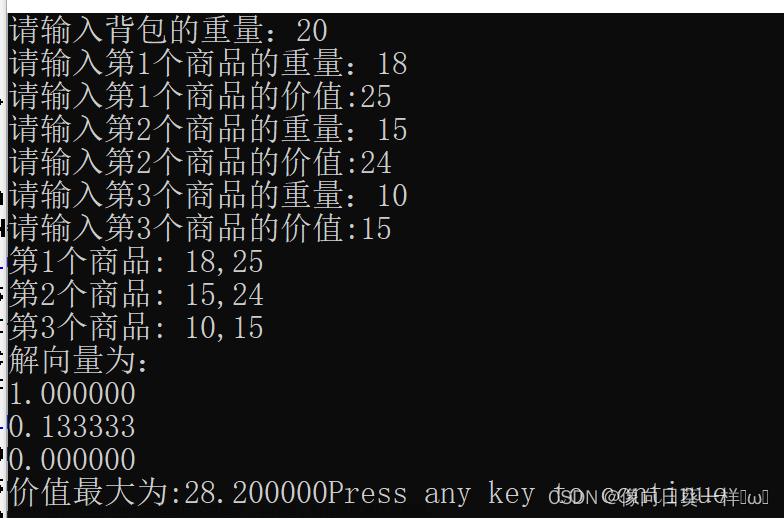
}运行结果
 文章来源:https://www.toymoban.com/news/detail-510984.html
文章来源:https://www.toymoban.com/news/detail-510984.html
ps:由于笔者水平有限,并且也是刚刚学习分支限界法,花了很长的时间写+调试,若有错误,敬请指正。文章来源地址https://www.toymoban.com/news/detail-510984.html
到了这里,关于分支限界法解决0/1背包问题(C语言实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!