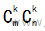这篇具有很好参考价值的文章主要介绍了过渡矩阵、线性变换矩阵在对应基下坐标的求法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
在求过渡矩阵时尤其要注意的是过渡矩阵和哪个向量组相乘得另一个向量组。
一般情况下，若描述是：求A到B的过渡矩阵，则形式应当是B=AC，其中C为过渡矩阵。
下面的这个例题就是求过渡矩阵和基下的坐标。
下面的这个例子主要是求线性变换矩阵在相应的基下的坐标。
文章来源地址https://www.toymoban.com/news/detail-511006.html
文章来源：https://www.toymoban.com/news/detail-511006.html
到了这里，关于过渡矩阵、线性变换矩阵在对应基下坐标的求法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
x = [ x y ] boldsymbol{x} =begin{bmatrix}x\\\\yend{bmatrix} x = [ x y ] 1. 平移变换 [ x ′ y ′ ] = [ x y ] + [ a b ] begin{bmatrix}x\\\'\\\\y\\\'end{bmatrix} = begin{bmatrix}x\\\\yend{bmatrix} + begin{bmatrix}a\\\\bend{bmatrix} [ x ′ y ′ ] = [ x y ] + [ a b ] 将向量 [ a b ] begin{bmatrix}a\\\\bend{bmatrix} [ a b ] 加到 [
💕 恭喜本博客浏览量达到两百万，CSDN内容合伙人，CSDN人工智能领域实力新星~ 🧡 本文章为2021版本迭代更新版本，在结合有效知识的基础上对文章进行合理的增加，使得整个文章时刻顺应时代需要 🧡 本专栏将通过系统的深度学习实例，从可解释性的角度对深度学习的原理
一个平面向量，用a(1,0),b( − 1 2 , 3 2 -frac{1}{2},frac{sqrt3}{2} − 2 1 , 2 3 ),c( − 1 2 , − 3 2 -frac{1}{2},-frac{sqrt3}{2} − 2 1 , − 2 3 )这三个单位向量线性表示，显然有无穷多种解，即某一特解加上N倍的(a+b+c)零向量 根据a,b,c向量的空间对称性可知 a ⃗ + b ⃗ + c ⃗
在线性代数中，逆矩阵是一个非常重要且有趣的概念。一个 n 阶方阵 A 的逆矩阵，记作 A^-1，是指存在另一个 n 阶方阵 B，使得 A 和 B 的乘积等于单位矩阵 E，即： A * B = E 或者等价地： B * A = E 这里，E 表示 n 阶单位矩阵，其对角线元素全为 1，其他位置的元素全为 0。 逆矩阵
本文讨论 3阶矩阵 的特征值的快速求法。 分为速写特征多项式和速解方程两部分。 速写特征多项式 不妨令： A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] boldsymbol{A}=left[begin{array}{lll} a_{11} a_{12} a_{13} \\\\ a_{21} a_{22} a_{23} \\\\ a_{31} a_{32} a_{33} end{array}right] A = a 11 a 21 a 31
在 n n n 维欧几里得空间 V V V 中，有子空间 W W W . 如果用自然基 ( e i ) 1 ≤ i ≤ n (mathbf{e}_i)_{1leq i leq n} ( e i ) 1 ≤ i ≤ n ，设 W = s p a n ( w 1 , … , w d ) ( 0 d n ) W=mathrm{span}(w_1, ldots, w_d); (0 d n) W = span ( w 1 , … , w d ) ( 0 d n ) . 将这个基作Schmidt正交化（并单位化
线性代数之矩阵秩的求法 在m×n的矩阵A中，任取k行、k列(k小于等于m、k小于等于n)，位于这些行和列交叉处的 个元素，在不改变原有次序的情况下组成的矩阵叫做矩阵A的k阶子式。 不难发现矩阵A有个 个k阶子式。 比如有矩阵A 比如取第1行，第3行，第1列，第4列交叉上的元素
玩转线性代数(21)线性方程组解的判断与求法的笔记，相关证明以及例子见原文 对n元线性方程组 A x = b Ax=b A x = b ，A为系数矩阵， B = ( A ∣ b ) B=(A|b) B = ( A ∣ b ) 为增广矩阵，则有 （1） A x = b Ax=b A x = b 无解 ⇔ R ( A ) R ( A , b ) Leftrightarrow R(A)lt R(A,b) ⇔ R ( A ) R ( A , b ) ; （2）
前言：基变换在做图像压缩等计算的时候，经常用到。基变换和相似矩阵的定义也有非常密切的联系：基变换的本质就是变换了基向量的一个关联计算，在最小二乘的算法里面，通过选择正确的基可以将计算进行简化。 而正确的的特征向量和特征值的确定，又和本节的基变
本节主要记录ardupilot 中坐标变换矩阵和坐标系变换矩阵的区别，这里非常重要，特别是进行姿态误差计算时，如果理解错误，很难搞明白后面算法。 坐标变换矩阵的本质含义： 是可以把一个向量的坐标从一个坐标系变换到另外一个坐标系。 而坐标系变换矩阵含义： 两个坐
