源码或数据集请点赞关注收藏后评论区留言或者私信博主要
由于独特的设计结构 LSTM适合于处理和预测时间序列中间隔和延迟非常长的重要事件。
LSTM是一种含有LSTM区块(blocks)或其他的一种类神经网络,文献或其他资料中LSTM区块可能被描述成智能网络单元,因为它可以记忆不定时间长度的数值,区块中有一个gate能够决定input是否重要到能被记住及能不能被输出output
LSTM有很多个版本,其中一个重要的版本是GRU(Gated Recurrent Unit),根据谷歌的测试表明,LSTM中最重要的是Forget gate,其次是Input gate,最次是Output gate。
介绍完LSTM的基本内容 接下来实战通过LSTM来预测股市收盘价格
先上结果
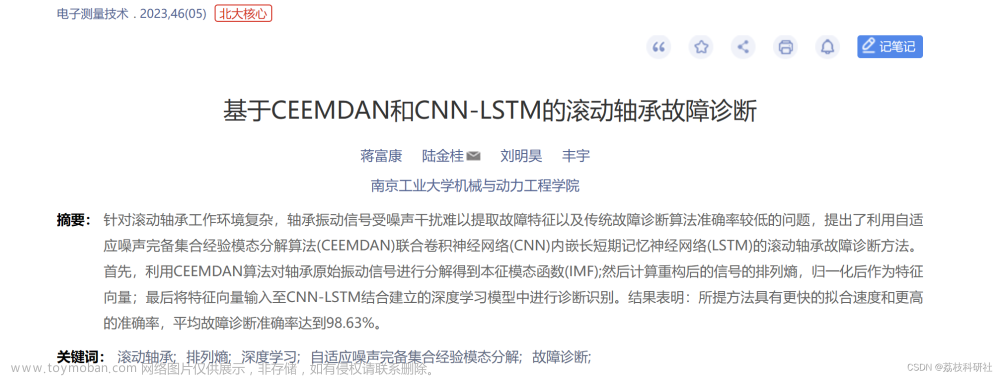
1:随着训练次数增加损失函数的图像如下 可以看出基本符合肘部方法 但是局部会产生突变


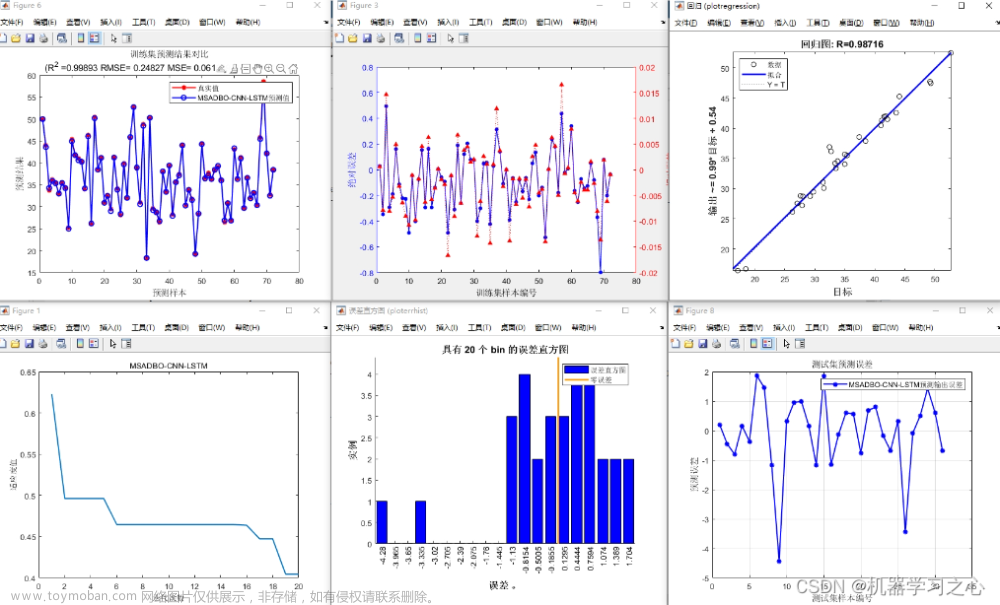
2:预测结果如下 红色的是预测值 蓝色的是真实值 可以看出除了某几个极值点正确率较高
 文章来源:https://www.toymoban.com/news/detail-511500.html
文章来源:https://www.toymoban.com/news/detail-511500.html
代码如下文章来源地址https://www.toymoban.com/news/detail-511500.html
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.utils.data import DataLoader, Dataset
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
def read_dataset(dataset_type):
assert dataset_type == "train" or dataset_type == "test"
df = pd.read_csv(stock_market_price_{}.csv'.format(dataset_type)) # 读入股票数据
data = np.array(df['close']) # 获取收盘价序列
data = data[::-1] # 反转,使数据按照日期先后顺序排列
normalize_data = (data - np.mean(data)) / np.std(data) # 标准化
normalize_data = normalize_data[:, np.newaxis] # 增加维度
X, y = [], []
for i in range(len(normalize_data) - time_step):
_x = normalize_data[i:i + time_step]
_y = normalize_data[i + time_step]
X.append(_x.tolist())
y.append(_y.tolist())
# plt.figure()
# plt.plot(data)
# plt.show() # 以折线图展示data
return X, y
# 实验参数设置
time_step = 7 # 用前七天的数据预测第八天
hidden_size = 4 # 隐藏层维度
lstm_layers = 1 # 网络层数
batch_size = 64 # 每一批次训练多少个样例
input_size = 1 # 输入层维度
output_size = 1 # 输出层维度
lr = 0.05 # 学习率
class myDataset(Dataset):
def __init__(self, x, y):
self.x = x
self.y = y
def __getitem__(self, index):
return torch.Tensor(self.x[index]), torch.Tensor(self.y[index])
def __len__(self):
return len(self.x)
class LSTM(nn.Module):
def __init__(self, input_size, output_size, hidden_size, device):
super(LSTM, self).__init__()
self.input_size=input_size
self.output_size=output_size
self.hidden_size=hidden_size
self.device=device
def _one(a,b):
return nn.Parameter(torch.FloatTensor(a,b).to(self.device))
def _three():
return(_one(input_size,hidden_size),
_one(hidden_size,hidden_size),
nn.Parameter(torch.zeros(hidden_size).to(self.device)))
self.W_xi,self.W_hi,self.b_i=_three()
self.W_xf, self.W_hf, self.b_f = _three()
self.W_xo, self.W_ho, self.b_o = _three()
self.W_xc, self.W_hc, self.b_c = _three()
self.W_hq=_one(hidden_size,output_size)
self.b_q=nn.Parameter(torch.zeros(output_size).to(self.device))
self.params=[self.W_xi,self.W_hi,self.b_i,self.W_xf, self.W_hf, self.b_f, self.W_xo, self.W_ho, self.b_o,self.W_xc, self.W_hc, self.b_c,
self.W_hq,self.b_q]
for param in self.params:
if param.dim()==2:
nn.init.xavier_normal_(param)
def init_lstm_state(self, batch_size):
return (torch.zeros((batch_size, self.hidden_size), device=self.device),
torch.zeros((batch_size, self.hidden_size), device=self.device))
def forward(self, seq):
(H,C)=self.init_lstm_state(seq.shape[0])
for step in range(seq.shape[1]):
X=seq[:,step,:]
I=torch.sigmoid((X@self.W_xi)+(H@self.W_hi)+self.b_i)
F = torch.sigmoid((X @ self.W_xf) + (H @ self.W_hf) + self.b_f)
O = torch.sigmoid((X @ self.W_xo) + (H @ self.W_ho) + self.b_o)
C_tilda=torch.tanh(torch.matmul(X.float(),self.W_xc)+torch.matmul(H.float(),self.W_hc)+self.b_c)
C=F*C+I*C_tilda
H=O*torch.tanh(C)
Y=(H@self.W_hq)+self.b_q
return Y,(H,C)
X_train, y_train = read_dataset('train')
X_test, y_test = read_dataset('test')
train_dataset = myDataset(X_train, y_train)
test_dataset = myDataset(X_test, y_test)
train_loader = DataLoader(train_dataset, batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, 1)
# 设定训练轮数
num_epochs = 50
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
hist = np.zeros(num_epochs)
model = LSTM(input_size, output_size, hidden_size, device)
# 定义优化器和损失函数
optimiser = torch.optim.Adam(model.parameters(), lr=lr) # 使用Adam优化算法
loss_func = torch.nn.MSELoss(reduction='mean') # 使用均方差作为损失函数
for epoch in range(num_epochs):
epoch_loss = 0
for i, data in enumerate(train_loader):
X, y = data
pred_y, _ = model(X.to(device))
loss = loss_func(pred_y, y.to(device))
optimiser.zero_grad()
loss.backward()
optimiser.step()
epoch_loss += loss.item()
print("Epoch ", epoch, "MSE: ", epoch_loss)
hist[epoch] = epoch_loss
plt.plot(hist)
plt.show()
# 测试
model.eval()
result = []
for i, data in enumerate(test_loader):
X, y = data
pred_y, _ = model(X.to(device))
result.append(pred_y.item())
plt.plot(range(len(y_test)), y_test, label="true_y", color="blue")
plt.plot(range(len(result)), result, label="pred_y", color="red")
plt.legend(loc='best')
plt.show()
到了这里,关于LSTM神经网络实现对股市收盘价格的预测实战(python实现 附源码 超详细)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!