图的几个基本概念：连通图、强连通图、完全图等-Toy模板网

这篇具有很好参考价值的文章主要介绍了图的几个基本概念：连通图、强连通图、完全图等。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

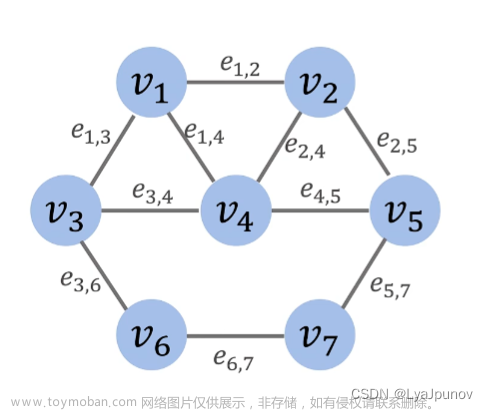
1、<v,w>表示v到w的一条弧，v是弧尾、w是弧头

2、无向完全图：任意两个顶点之间都有边，n个顶点有1/2 *n *(n-1)条边；

3、有向完全图：任意两个顶点之间都存在方向相反的两条弧 n个顶点有 n *(n-1) 条边；

4、子图：假设有两个图G=（V,{E}）和g=（v,{e}）,如果v⊆V，e⊆E，则称g为G的子图；

例：假设有图G=（V,{E}），顶点集A⊆V，B⊆E，则A和{B}构成G的子图。

答：错误，因为A和B未必能构成图。定义中g是G的子图，是因为给条件时已经明确g是图。

5、简单路径：序列中顶点不重复出现的路径；

6、简单回路或简单环：除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路；

7、在无向图G中，如果从顶点v到顶点v1有路径，则称v和v1是连通的；

8、连通图：图中任意两个顶点vi,vj都是连通的；

9、连通分量：指的是无向图中的极大连通子图；

10、在有向图G中，如果对于每对vi,vj(vi != vj)，从vi到vj和从vj到vi都存在路径，则称G是强连通图

11、一个连通图的生成树是一个极小连通子图;

12、Ve()【事件也就是顶点】：事件最早发生时间，从前往后，取最大值

Vl()：事件最晚发生时间，从后往前推，取最小值

e()【活动也就是弧】：活动最早开始时间，e=<v1,v2>，e(i) = Ve(v1);

l()：活动最晚发生时间：从后往前，l=Vl - 活动时间

d(i)=l(i) - e(i);d=0为关键活动【关键路径可能有许多条，只有减少关键路径上共享的活动才可能减少工期】文章来源地址https://www.toymoban.com/news/detail-511549.html

到了这里，关于图的几个基本概念：连通图、强连通图、完全图等的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

图的几个基本概念：连通图、强连通图、完全图等