高斯混合模型（GMM）及EM算法---MATLAB程序-Toy模板网

这篇具有很好参考价值的文章主要介绍了高斯混合模型（GMM）及EM算法---MATLAB程序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

大家喜欢的话记得关注、点赞、收藏哦~

高斯混合模型（Gaussian Mixed Model,GMM）是由多个高斯分布函数组成的线性组合。理论上，GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同分布的情况。---转自：http://t.csdn.cn/SPEcN

高斯混合模型（GMM）及EM算法---MATLAB程序

设随机变量 X服从混合高斯分布（Mixture Gaussian Distribution），其概率密度函数如下所示：

高斯混合模型（GMM）及EM算法---MATLAB程序

其中，K为分量数，若用两个二维高斯分布来表示，则有分量数K = 2 ；为混合系数（mixture coefficient），可以看作每个分量的权重，也可以看作每个分量被选中的概率，混合系数满足如下关系：

高斯混合模型（GMM）及EM算法---MATLAB程序

读到这里，想必各位心中都会自然而然地产生一个问题：各分量的分布参数和混合系数要怎么确定？这里就需要引入最大期望算法（Expectation-maximization algorithm,EM）对各参数进行估计！！！（核心）

为了确保文章的完整性，GMM的参数估计过程引用了博客http://t.csdn.cn/SPEcN的部分内容：

引入一个新的K维随机变量z（0-1变量），表示第k个分量被选中的概率为，满足如下关系：

高斯混合模型（GMM）及EM算法---MATLAB程序

假设之间独立同分布，我们可以写出z的联合概率分布：

高斯混合模型（GMM）及EM算法---MATLAB程序

被选中分量的概率密度函数可以写作如下形式：

高斯混合模型（GMM）及EM算法---MATLAB程序

进而，

高斯混合模型（GMM）及EM算法---MATLAB程序

上面分别给出了和，根据全概率公式，可以求出

高斯混合模型（GMM）及EM算法---MATLAB程序

其中，表示对z的K种情况进行累加。上式与GMM的定义式具有相同的形式，但上式引入了新的变量z，通常称为隐含变量（latent variable）。『隐含』的意义是：我们知道数据可以分成两类，但是随机抽取一个数据点，我们不知道这个数据点属于第一类还是第二类，有多少概率属于第一类，有多少概率属于第二类，它的归属我们观察不到，因此引入一个隐含变量z来描述这个现象。（转自：http://t.csdn.cn/SPEcN，我感觉这段话写得特别好）

EM算法即可用于求解具有隐含变量的参数估计问题。

在贝叶斯的思想下，是先验概率，是似然概率，是后验概率。为方便使用EM算法估计GMM模型的参数，需要推导后验概率的表达式，如下所示：

高斯混合模型（GMM）及EM算法---MATLAB程序

至此，我们完成了所有的前期准备工作，接下来引入EM算法以估计GMM模型的各个参数。

EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐性变量。

EM算法经过两个步骤交替进行计算：

第一步：计算期望（E步），利用对隐藏变量的现有估计值，计算其最大似然估计值；
第二步：最大化（M步），最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。（转自：http://t.csdn.cn/gTdx1）

GMM模型中待估计的参数有，将定义式改写为以下形式

高斯混合模型（GMM）及EM算法---MATLAB程序

写出上式的极大似然函数：

高斯混合模型（GMM）及EM算法---MATLAB程序

对各参数求偏导并令导数为0可得（推导过程详见 http://t.csdn.cn/iRa9n ）

高斯混合模型（GMM）及EM算法---MATLAB程序

其中，

高斯混合模型（GMM）及EM算法---MATLAB程序

算法流程如下：

1) 确定分量数K，利用k-means算法对样本进行划分，计算各分量对应样本的均值和协方差作为和的初值，取1/K，即各分量的权重相等

2） E步：根据当前的,和计算后验概率

高斯混合模型（GMM）及EM算法---MATLAB程序

3) M步：根据步骤2）中的重新计算 ,和

高斯混合模型（GMM）及EM算法---MATLAB程序

其中，

高斯混合模型（GMM）及EM算法---MATLAB程序

4) 计算极大似然函数

高斯混合模型（GMM）及EM算法---MATLAB程序

5) 检查极大似然函数是否收敛，若收敛，输出当前的,和，否则返回步骤2)。

本文的MATLAB代码如下：

一维数据：

clear all
clc
close all

samples = [normrnd(5,2,[1000,1]);normrnd(0,1,[1000,1])];%这里的sigma是标准差standard deviation

D=size(samples,2);
N=size(samples,1);

K=2;%用K个正态分布拟合
Pi=ones(1,K)/K;
Miu=cell(K,1);
Sigma2=cell(K,1);

%% %K均值聚类确定初值
[idx,center]=kmeans(samples,K);
for i=1:K
    miu0=center(i,:);
    sigma0=var(samples(find(idx==i),:));
    Miu{i,1}=miu0;
    Sigma2{i,1}=sigma0;
end

beta=inf;
likelihood_function_value=0;
record=[];
%% %EM算法
while(1)
    %% %E步
    gama=zeros(N,K);
    samples_pd=zeros(N,K);
    for j=1:K
        samples_pd(:,j)=normpdf(samples,Miu{j,1},sqrt(Sigma2{j,1}));
    end
    for i=1:N
        for j=1:K
            gama(i,j)=Pi(j)*samples_pd(i,j)/(Pi*samples_pd(i,:)');
        end
    end
    
    likelihood_function_value_old=likelihood_function_value;
    likelihood_function_value=sum(log(sum(samples_pd.*repmat(Pi,N,1),1)));
    record=[record,likelihood_function_value];
    beta=abs(likelihood_function_value-likelihood_function_value_old);    
    if beta<0.0001
        plot(1:length(record),record)
        break
    end
    %% %M步
    Nk=sum(gama,1);
    for j=1:K
        Miu{j,1}=zeros(1,D);
        Sigma2{j,1}=zeros(D,D);
        for i=1:N
            Miu{j,1}=Miu{j,1}+gama(i,j)*samples(i,:)/Nk(j);
        end 
        for i=1:N
            Sigma2{j,1}=Sigma2{j,1}+(gama(i,j)*(samples(i,:)-Miu{j,1})'*(samples(i,:)-Miu{j,1}))/Nk(j);
        end
    end
    Pi=Nk/N;
end



X = [min(samples(:,1)):0.01:max(samples(:,1))]';
YX=zeros(size(X,1),K);
for j=1:K
    YX(:,j)=normpdf(X,Miu{j,1},sqrt(Sigma2{j,1}));
end

figure(2)
[count,centers]=hist(samples,100); 
bar(centers,count,'FaceColor',[0.72,0.89,0.98])
hold on
plot(X, YX(:,1)/max(YX(:,1))*max(count),'color',[0.85,0.33,0.10],'linewidth',2)
plot(X, YX(:,2)/max(YX(:,2))*max(count),'color',[0.93,0.69,0.13],'linewidth',2)
YX = sum(YX.*repmat(Pi,size(X,1),1),2);
YX=YX/max(YX)*max(count);
plot(X,YX,'color',[0.00,0.45,0.74],'linewidth',2)

高斯混合模型（GMM）及EM算法---MATLAB程序

多维数据：

clear all
clc
close all


mu1 = [5,2];     % 均值
sigma1 = [1  , 0.9; 
         0.9  , 1];  % 协方差
mu2 = [2,5];     % 均值
sigma2 = [1  , 0.45; 
         0.45  , 1];  % 协方差 
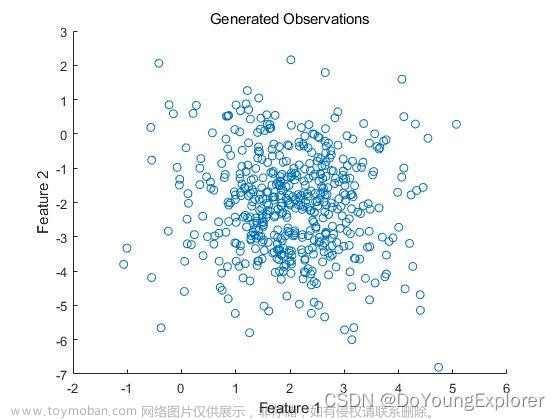
samples = [mvnrnd(mu1,sigma1,1000);mvnrnd(mu2,sigma2,1000)];%这里的sigma是协方差covariances


D=size(samples,2);
N=size(samples,1);

K=2;%用K个正态分布拟合
Pi=ones(1,K)/K;
Miu=cell(K,1);
Sigma=cell(K,1);

[idx,center]=kmeans(samples,K);
for i=1:K
    miu0=center(i,:);
    sigma0=cov(samples(find(idx==i),:));
    Miu{i,1}=miu0;
    Sigma{i,1}=sigma0;
end

beta=inf;
likelihood_function_value=0;
record=[];
%% %EM算法
while(1)
    %% %E步
    gama=zeros(N,K);
    samples_pd=zeros(N,K);
    for j=1:K
        samples_pd(:,j)=mvnpdf(samples,Miu{j,1},Sigma{j,1});
    end
    for i=1:N
        for j=1:K
            gama(i,j)=Pi(j)*samples_pd(i,j)/(Pi*samples_pd(i,:)');
        end
    end
    
    likelihood_function_value_old=likelihood_function_value;
    likelihood_function_value=sum(log(sum(samples_pd.*repmat(Pi,N,1),1)));
    record=[record,likelihood_function_value];
    beta=abs(likelihood_function_value-likelihood_function_value_old);    
    if beta<0.001
        plot(1:length(record),record)
        break
    end
    %% %M步
    Nk=sum(gama,1);
    for j=1:K
        Miu{j,1}=zeros(1,D);
        Sigma{j,1}=zeros(D,D);
        for i=1:N
            Miu{j,1}=Miu{j,1}+gama(i,j)*samples(i,:)/Nk(j);
        end
        for i=1:N
            Sigma{j,1}=Sigma{j,1}+(gama(i,j)*(samples(i,:)-Miu{j,1})'*(samples(i,:)-Miu{j,1}))/Nk(j);
        end
    end
    Pi=Nk/N;
end

X = gridsamp([min(samples(:,1)) min(samples(:,2));max(samples(:,1)) max(samples(:,2))], 40);
YX0=zeros(size(X,1),K);
for j=1:K
    YX0(:,j)=mvnpdf(X,Miu{j,1},Sigma{j,1});
end

X1 = reshape(X(:,1),40,40); X2 = reshape(X(:,2),40,40);
YX = reshape(YX0(:,1), size(X1));
figure(2), mesh(X1, X2, YX,'edgecolor',[0.85,0.33,0.10])
YX = reshape(YX0(:,2), size(X1));
hold on,mesh(X1, X2, YX,'edgecolor',[0.93,0.69,0.13])
YX = reshape(sum(YX0.*repmat(Pi,size(X,1),1),2), size(X1));
figure(3),mesh(X1, X2, YX,'edgecolor',[0.00,0.45,0.74])

高斯混合模型（GMM）及EM算法---MATLAB程序文章来源地址https://www.toymoban.com/news/detail-512407.html

function  S = gridsamp(range, q)
%GRIDSAMP  n-dimensional grid over given range
%
% Call:    S = gridsamp(range, q)
%
% range :  2*n matrix with lower and upper limits
% q     :  n-vector, q(j) is the number of points
%          in the j'th direction.
%          If q is a scalar, then all q(j) = q
% S     :  m*n array with points, m = prod(q)

% hbn@imm.dtu.dk  
% Last update June 25, 2002

[mr n] = size(range);    dr = diff(range);
if  mr ~= 2 | any(dr < 0)
  error('range must be an array with two rows and range(1,:) <= range(2,:)')
end 
sq = size(q);
if  min(sq) > 1 | any(q <= 0)
  error('q must be a vector with non-negative elements')
end
p = length(q);   
if  p == 1,  q = repmat(q,1,n); 
elseif  p ~= n
  error(sprintf('length of q must be either 1 or %d',n))
end 

% Check for degenerate intervals
i = find(dr == 0);
if  ~isempty(i),  q(i) = 0*q(i); end

% Recursive computation
if  n > 1
  A = gridsamp(range(:,2:end), q(2:end));  % Recursive call
  [m p] = size(A);   q = q(1);
  S = [zeros(m*q,1) repmat(A,q,1)];
  y = linspace(range(1,1),range(2,1), q);
  k = 1:m;
  for  i = 1 : q
    S(k,1) = repmat(y(i),m,1);  k = k + m;
  end
else    
  S = linspace(range(1,1),range(2,1), q).';
end

到了这里，关于高斯混合模型（GMM）及EM算法---MATLAB程序的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！