一、转置矩阵
假设矩阵 A 如下表示:

则其转置矩阵表示为:

二、对称矩阵
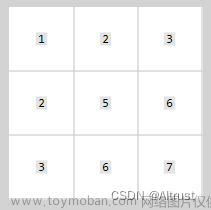
若矩阵 B 与其转置矩阵相等,则称矩阵 B 为对称矩阵,如:

三、反对称矩阵
若矩阵 C 与其转置矩阵取负后相等,则称矩阵 C 为反对称矩阵,其对角线元素的值为0,如:

四、向量的反对称矩阵
分别定义两个向量如下:

对两个向量进行叉乘得到:
 文章来源:https://www.toymoban.com/news/detail-512981.html
文章来源:https://www.toymoban.com/news/detail-512981.html
则向量的反对称矩阵为:
 文章来源地址https://www.toymoban.com/news/detail-512981.html
文章来源地址https://www.toymoban.com/news/detail-512981.html
到了这里,关于转置矩阵、对称矩阵、反对称矩阵以及向量的反对称矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!





![[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置)](https://imgs.yssmx.com/Uploads/2024/02/435123-1.png)





