矩阵标准化处理(内附MATLAB代码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了矩阵标准化处理(内附MATLAB代码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

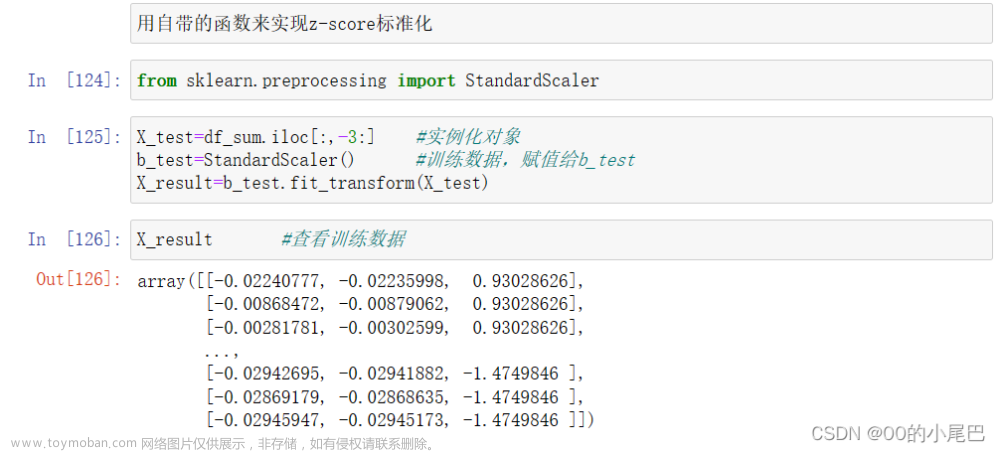
矩阵指标标准化处理

文章目录

矩阵指标标准化处理

1.原理

2.代码实现

2.1正向指标标准化

2.2负向指标标准化

3.运行结果

3.1 工作区变量

3.2 矩阵R标准化结果

4.总结

1.原理

2.代码实现

2.1正向指标标准化

R=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];

[rows,cols]=size(R);   % 输入矩阵的大小,rows为行数（对象个数），cols为列数（指标个数）

Rmin = min(R);         %矩阵中最小行
Rmax = max(R);         %矩阵中最大行
A = max(R) - min(R);   %分母 矩阵中最大行减最小行

y = R - repmat(Rmin,rows,1);      %分子 R矩阵每一行减去最小行
for j = 1 : cols                  %该循环用于标准化处理 分子/分母
     y(:,j) = y(:,j)/A(j);
end
S = sum(y,1);                     %列之和（用于列归一化）        
for i = 1 : cols                  %该循环用于列的归一化
    Y(:,i) = y(:,i)/S(i); 
end
Y                                 %打印R矩阵正向指标标准化处理结果

2.2负向指标标准化

R=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
[rows,cols]=size(R);   % 输入矩阵的大小,rows为行数（对象个数），cols为列数（指标个数）

Rmin = min(R);         %矩阵中最小行
Rmax = max(R);         %矩阵中最大行
A = max(R) - min(R);   %分母 矩阵中最大行减最小行

y1 = repmat(Rmax,rows,1) - R;     %分子 最大行减去R矩阵每一行

for j = 1 : cols                  %该循环用于负向指标标准化处理 分子/分母
     y1(:,j) = y1(:,j)/A(j);
end
S = sum(y1,1);                    %列之和（用于列归一化）
for i = 1 : cols                  %该循环用于列的归一化
    Y1(:,i) = y1(:,i)/S(i); 
end
Y1;                               %打印矩阵负向指标标准化处理结果