矩阵理论| 特殊矩阵：正定矩阵-Toy模板网

这篇具有很好参考价值的文章主要介绍了矩阵理论| 特殊矩阵：正定矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

正定矩阵Positive definite matrix

实数域中，满足 $\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0)$ 的矩阵 $\boldsymbol{A}$ 就是正定矩阵；
在复数域，满足 $\mathbf{x}^{H} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0)$ 的矩阵 $\boldsymbol{A}$ 就是正定矩阵（下面谈论的都是复正定矩阵）

注意，当谈论“正定矩阵”，一般默认的前提是矩阵已经是“（实）对称/（复）Hermite矩阵”

ps.
①严格意义上，对于实矩阵，正定矩阵不一定是对称的，而应该说：“实对称正定矩阵”通常简称为正定矩阵
因为从更广的定义上来说，只要满足 $\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0)$ 就是正定矩阵
但是，我们习惯将对称性纳入正定矩阵的定义，一方面因为实对称正定矩阵拥有良好性质，另一个原因是实对称正定矩阵的分析就足以应付其他一般的正定矩阵（原理：任何矩阵 $\boldsymbol{B}$ 的二次型均可被化为一个对称矩阵的等价二次型： $\mathbf{x}^{T} \boldsymbol{B} \mathbf{x}=\frac{1}{2}\mathbf{x}^{T}(\boldsymbol{B}+\boldsymbol{B}^T)\mathbf{x}$ ，其中 $\boldsymbol{A}=\frac{1}{2}(\boldsymbol{B}+\boldsymbol{B}^T)$ 是对称矩阵）
②对于复矩阵，正定矩阵一定是Hermite矩阵：“复Hermite正定矩阵”=复正定矩阵
i.e. $\boldsymbol{A}$ 为Hermite矩阵 $\iff$ 对于任意 $\bold x\in\mathbb C^n$ ，二次型 $\boldsymbol{x^HAx}$ 为实数
原因详见：正定矩阵的性质与判别方法

正定矩阵的性质和判别

先简单回顾对称矩阵的特殊性质：
①特征值为实数；
②拥有一套正交特征向量；
③正 / 负主元的数目等于正 / 负特征值的数目

正定矩阵在此基础上，有以下良好性质：

$\mathbf A$ 为正定矩阵 $\iff$ 所有特征值都为正实数
推论： $\mathbf A$ 的行列式>0（必然可逆）、迹>0
$\mathbf A$ 为正定矩阵 $\iff$ 所有主元pivot都为正实数
$\mathbf A$ 为正定矩阵 $\iff$ 左上角的所有任意k阶（1<=k<=n）顺序主子式(i.e.左上角的子矩阵的行列式)均为正
$\mathbf A$ 为正定矩阵 $\iff$ 存在可逆矩阵 $\mathbf B$ 使得 $\mathbf A=\mathbf B^H\mathbf B$
ps. 对任意矩阵 $\mathbf B$ ， $\mathbf B^H\mathbf B$ 、 $\mathbf B\mathbf B^H$ 至少为半正定矩阵（原因： $\mathbf B^H\mathbf B$ 可能不满秩，从而有0特征值）
当 $\mathbf B$ 列满秩 $\Rightarrow \mathbf B^H\mathbf B$ 为正定矩阵（原因： $\mathbf{x}^{T} (\mathbf B^T \mathbf B)\mathbf{x}=(\mathbf B\mathbf{x})^T\mathbf B\mathbf{x}$ ，而 $\mathbf B$ 列满秩时必有 $(\mathbf B\mathbf{x})\neq 0$ ）
当 $\mathbf B$ 为可逆方阵 $\iff \mathbf B^H\mathbf B$ 为正定矩阵

证明：
必要性：令 $B=\Lambda^{1 / 2} U^{H}$ ，则有 $\Lambda U^{H}=\left(U \Lambda^{1 / 2}\right)\left(\Lambda^{1 / 2} U^{H}\right) )=B^{H} B$
充分性：若 $\mathbf B$ 可逆， $\mathbf B$ 的零空间为{0}，则对任意非零向量 $\mathbf x$ 必有 $\mathbf{y}=\mathbf B\mathbf{x} \neq \mathbf{0}$ ，进而有 $\mathbf{x}^{H} A \mathbf{x}=\mathbf{x}^{H} B^{H} B \mathbf{x}=\mathbf{y}^{H} \mathbf{y}>0$

上一条的推论： $\mathbf A$ 为正定矩阵 $\iff$ 存在可逆下三角矩阵 $\mathbf L$ 使得 $\mathbf A=\mathbf L\mathbf L^H$ （Cholesky 分解）
详见：Cholesky 分解
$\mathbf A$ 为正定矩阵 $\Rightarrow$ $\mathbf A^{-1}$ 、 $\mathbf A^{k}$ 、 $\mathbf A$ 的任意主子阵（取出若干个第i行+第i列组合得到的子矩阵）都是正定矩阵‘
$\mathbf A$ 为正定矩阵 $\Rightarrow$ $det(\mathbf A)\le a_{11}...a_{nn}$

这些性质的证明：正定矩阵的性质与判别方法

正定矩阵的几何意义

（下面在实数域讨论，在复数域可以类似推广）

正定矩阵 $\boldsymbol{A}$ 满足 $\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0)$ ，其几何意义可以从三个角度来解释：文章来源地址https://www.toymoban.com/news/detail-515226.html

非零向量 $\mathbf{x}$ 与线性变换后的向量 $\boldsymbol{A} \mathbf{x}$ 的夹角< $\pi/2$
$\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \Rightarrow\mathbf{x}^{T} (\boldsymbol{A} \mathbf{x})>0\Rightarrow\cos \theta=\frac{\mathbf{x}^{T}(A \mathbf{x})}{\|\mathbf{x}\|\|A \mathbf{x}\|}>0\Rightarrow\theta<\pi/2$
画图理解：
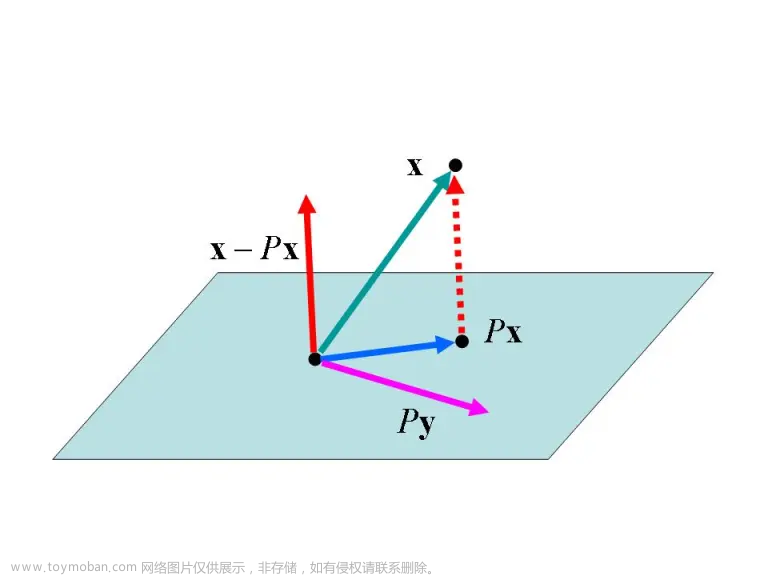
对于任意向量 $\mathbf{x}$ （我们画出了与之垂直的超平面 $P$ ），变换后的向量 $\boldsymbol{A} \mathbf{x}$ 与 $\mathbf{x}$ 都位于超平面 $P$ 的同一侧（ $\boldsymbol{A} \mathbf{x}$ 不是位于超平面 $P$ 内/ $P$ 的另一侧）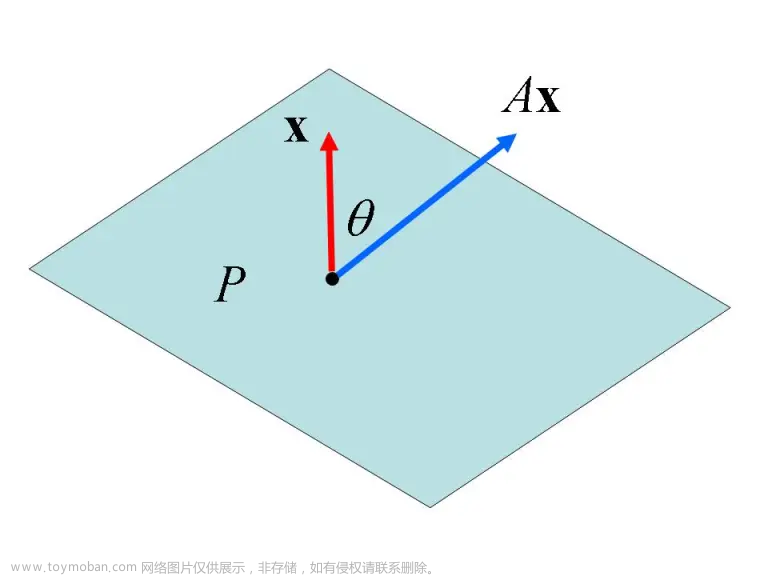
而正交投影矩阵满足 $\mathbf A^2=\mathbf A=\mathbf A^H$ ，这是半正定矩阵（因为存在酉矩阵 $\mathbf U$ 使得正交投影矩阵满足 $\mathbf A=\mathbf A^H=\mathbf U\mathbf U^H$ ，则 $\mathbf{x}^{H} \boldsymbol{A} \mathbf{x}=(\mathbf U^H\mathbf x)^H(\mathbf U^H\mathbf x)\geq 0$ ）；因而存在这样向量 $\mathbf{x}$ ，其投影后的结果 $\boldsymbol{A} \mathbf{x}$ 在与 $\mathbf{x}$ 垂直的超平面 $P$ 内
正定矩阵对应的线性变换，在一组合适的标准正交基下观察，表现为分別拉伸各主轴
由相似对角化 $\boldsymbol{A=Q\Lambda Q^T}$ 得，这个坐标系的主轴就是特征向量，而伸缩量就是特征值（全部大于0）
也可以将 $\boldsymbol{A=Q\Lambda Q^T}$ 解释为旋转+拉伸+旋转（旋转这个说法不是非常准确，前提是正交矩阵 $Q$ 的行向量必须适当排序，否则也可能包含镜像变换)