【手撕算法|动态规划系列No.1】leetcode1137. 第 N 个泰波那契数-Toy模板网

这篇具有很好参考价值的文章主要介绍了【手撕算法|动态规划系列No.1】leetcode1137. 第 N 个泰波那契数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

个人主页：平行线也会相交
欢迎点赞👍 收藏✨ 留言✉ 加关注💓本文由平行线也会相交原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

点击直接跳转到该题目

🍬题目描述

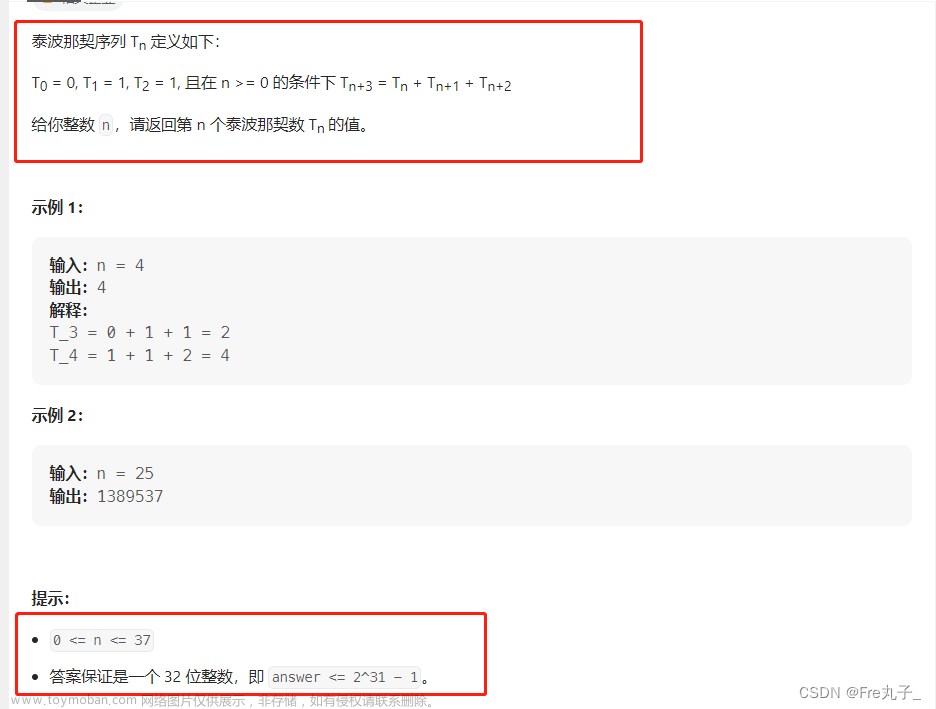
泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

示例 2：

输入：n = 25
输出：1389537

🍦动态规划算法原理+题目解析。

这里要求的是第n个泰波那契数，泰波那契数不同于斐波那契数，两者区别如下：

斐波那契数列是以0和1为初始值，每个数字是前两个数字的和，形成的数列是0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …。
泰波那契数列是以0、1和1为初始值，每个数字是前三个数字的和，形成的数列是0, 1, 1, 2, 4, 7, 13, 24, 44, …。

说白了，第n个泰波那契数其实就是前面3项加起来的和。用一个公式来表示就是Tn = Tn-3 + Tn-2 + Tn-1。

现在我们先来简单介绍一下什么是动态规划。

动态规划算法通过将问题分解成子问题，并利用子问题的解推导出更大规模问题的解，避免了重复计算，从而提高了算法的效率。

我们今后在练习动态规划的题目的时候，一般会按照如下几个步骤进行题目的分析、解答。请看：
步骤1（最重要）.状态表示

状态表示是什么意思呢？我们要先建立一个dp表（一般是一个一维数组或者二维数组），状态表示其实就是dp表中每个位置的具体含义。
那我们应该如果来求取题目的状态表示呢？状态表示又是怎么来的？这里给出了3种方法，请看：
①根据题目要求，题目怎么要求的我们就怎么来
②（重点）根据自己的经验+题目要求
③分析问题的过程中，发现了重复的子问题

【手撕算法|动态规划系列No.1】leetcode1137. 第 N 个泰波那契数

由于这个题目（第 N 个泰波那契数）比较简单，所以我们可以直接根据题目要求来得到题目的状态表示。在本题目中，dp表即dp[i]就表示第 N 个泰波那契数。

步骤2（最难）：状态转移方程

我们先来看看官方是怎么定义状态转移方程的，请看：找到子问题之间的递推关系，即通过已知子问题的解推导出更大规模的子问题的解。
其实说简单一点，就是求dp[i]等于什么：
在本题目中，dp[i]=d[i-3]+d[i-2]+dp[i-1]。

步骤3：初始化

步骤3就是根据状态转移方程来填表，而且必须保证填表的时候不能越界。
在本题目中，根据状态转移方程dp[i]=d[i-3]+d[i-2]+dp[i-1]来进行初始化，由于必须要保证不越界，所以根据题目要求，我们只需要初始化dp[0]=0、dp[1]=1、dp[2]=1

步骤4：填表顺序

为了填写当前状态的时候，所需要的状态已经计算过了。
这里举个例子，我们已经知道了dp[0]、dp[1]、dp[2]位置的状态，可以根据这三个位置的状态来填写dp[3]。但是我们如果想要知道dp[4]的话，我们就需要三个位置的状态（即dp[1]、dp[2]、dp[3]位置的状态）。

步骤5：返回值

由于这里dp[i]表示第i个泰波那契数，所以dp[n]就表示第n个泰波那契数。所以这里返回值很简单
，我们直接返回dp[i]就好了。

以上就是动态规划的几个基本的步骤。

🍰解题代码1

class Solution {
public:
    int tribonacci(int n) {

        //处理越界问题
        if(n==0) return 0;
        if(n==1||n==2) return 1;
        //创建dp表
        vector<int> dp(n+1);
        //初始化
        dp[0]=0,dp[1]=1,dp[2]=1;
        //填表
        for(int i = 3;i <= n;i++)
            dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
        //返回值
        return dp[n];
    }
};

🍔解题代码2（空间优化—滚动数组）

我们可以对本题进行一个空间优化，即利用滚动数组。
那这里是怎样一个空间优化呢？我们先来分析一下在哪里我们可以进行空间优化。

就比如说我们在求取dp[4]的值的时候需要用到dp[1]、dp[2]、dp[3]的值，而dp[0]的值是用不到的；
所以这里就造成了一部分空间的浪费。
在比如说，我们在求取dp[6]的值的时候需要用到dp[3]、dp[4]、dp[5]的值，而dp[0]、dp[1]、dp[2]的值是用不到的；所以这里一下子就造成了dp[0]、dp[1]、dp[2]所占空间的浪费。

【手撕算法|动态规划系列No.1】leetcode1137. 第 N 个泰波那契数

需要注意的是，当我们在进行变量a、b、c的赋值操作的时候，必须从前往后赋值，而不能从后往前赋值。

总结：当我们一次求取dp[i]的时候，前面的某些状态如果可以舍去，仅仅使用中间有效的若干个状态，这种情况我们就可以使用滚动数组来解决问题。
下面来看解题代码，请看：

class Solution {
    public int tribonacci(int n) {
        if(n==0) return 0;
        if(n==1||n==2) return 1;
        int a = 0, b = 1, c = 1, d = 0;
        for(int i = 3; i <= n; i++)
        {
            //滚动数组
            d = a + b + c;
            a = b; b = c; c = d;
        }
        return d;
    }
}