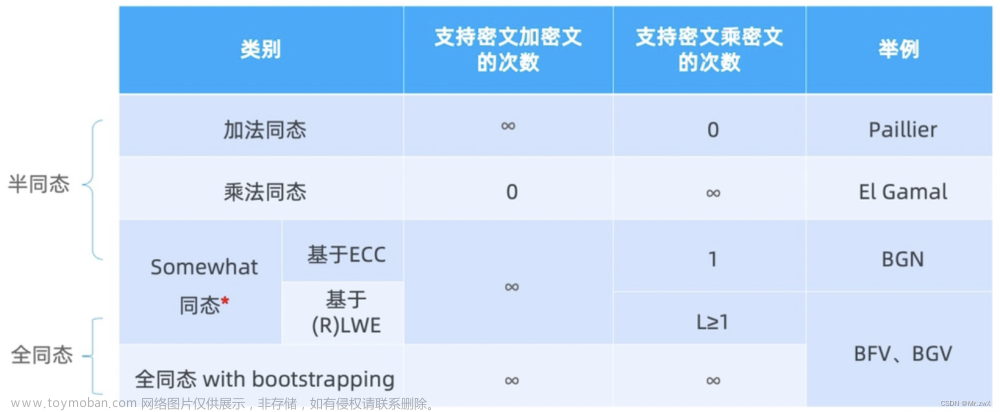
维吉尼亚加密
古典密码,属于多表加密。
-
怎么就是多表了?
维吉尼亚密码的加密算法实质是凯撒密码,因为他是先分好小组,然后用密钥串对应着分好组的每一个字母进行加密(因为一个凯撒表用密钥串的一个字母加密),当然是遵循下标相同的,比如秘钥为:abc,明文为qwer,然后明文可分组为qwe, r
然后加密就是不断迭代密钥和明文组,q对应密钥a,然后w对应密钥b,然后明文e对应密钥c,然后第一组遍历完了继续第二组,r对应密钥a,然后加密完成。注意这里即使不够分组也是照样加密,每组加密完成后密钥从头开始遍历
-
属于分组加密算法
按照密钥长度进行分组,但是每组字母都不是来自连续的明文或者密文
我们在分组之前要按照每一个密钥长度为一组,然后每一组的第一个为密钥第一个字母所加密,也就是凯撒加密。
如图:
密钥采用五个的字母: JANET
很明显就是将给出的信息,首先按照原来的顺序按照密钥长度5个分开,然后再根据每一个组的相同下标的字母给与之对应下标的密钥字母进行凯撒加密,比如每一小组的第一个组成的凯撒加密表就是用J加密的,因为秘钥中的第一个字母就是J,然后我们要在分好的小组里面全部的小组第一个都用J加密

-
密钥是一串字母
加密要将密钥转换为数字,因此就变成了每一组由密钥中每一个字母进行加密,所以就变成了多个凯撒密码加密,由此得来多表加密。
就好比分好组排好队之后每一个表去密钥串中领取自己对应组好的密钥(组号就是密钥的下标,每一个秘钥字母对应一个凯撒加密表)
加密算法
- 在这里采用查表的方式加密,事先生成一个26×26的凯撒的加密表,如图。
声明:其实这里可以采用传统的凯撒加密方式就是一个一个的移动,我这里之所以采用查表的方式首先是因为书本是这么写的,老师是这么教的,为何要查表我的理解是因为维吉尼亚加密算法是用于文本加密,字母很多的那种,如果我们采用一个个移动的话速度会大大减慢,但是我们事先有了这么一个二维表只需要使用下标即可,而且这个表设计的非常巧妙,无论你纵横怎么看都可以进行加密,因为我们凯撒是明文+密钥,所以比如这里的我们看横排a,然后用纵排的c加密,那么我得到的就是c,你也可以只用使用(a,c)进行查表。(同理解密表也用这个)
- 生成加解密表
- 这里的np是要下载numpy包
def generate_Dit(): p = 26 # 生成Vigenere表 Cipher_list = [] for row in range(p): for column in range(p): Cipher_list.append((row + column) % p) Cipher_list = np.asarray(Cipher_list) # 转为矩阵 # reshape成26*26矩阵,也即Vigenere表 Cipher_list = Cipher_list.reshape(p, p) return Cipher_list # 返回Vigenere表- 开始加密
- 分组打包
- 加密的时候采用二层循环进行加密
因为已经分好组了,只需要将每组分别取出,然后采用对应下标与密钥进行对应的凯撒加密即可(这里需要注意的是,我是采用了分好组的下标,所以我只需要取出每组然后再对每组进行循环,而第二层循环的下标我直接给到Key使用,这样保证了不会因为不够一组的数量而导致下标越界,毕竟我遍历的是分好的组,取出该组长度进行遍历,作为key下标,而不是遍历key,因为有的人会采用遍历key的方式给每一个明文加密,我这里用了自己的方法),拿到了密钥与密文就直接到26×26中查表即可,这个表已经写好了一个函数,直接调用即可。
def enCode(): saveMess = [] key = 'cipher' #密钥 n = len(key) tempch = [''] * n #用来开辟空间,然后转储给其他变量 count = 0 #计数器,防止分组出现不够然后需要将最后剩余的一并添加进去 for ch in mess: if ord('A') <= ord(ch) <= ord('Z') \ or ord('a') <= ord(ch) <= ord('z'): # 确保了只能是字母才能添加进去 tempch[count % n] = ch # count计数器,但是为了与分组数一致要%每组字母数 count += 1 if count % n == 0 and count != 0: saveMess.append(tempch[0:n + 1]) # 使用切片进行 tempch = [''] * n if count % n != 0: # 将最后剩下的也打包成一组 saveMess.append(tempch[0:(count % n)]) # 使用切片将最后一部分单开成一组出来添加 print(saveMess) # 加密 for ch in saveMess: for index in range(len(ch)): # 每一组单独加密 k = ord(key[index].upper()) - ord('A') # 每一个密钥都对应一个ch明文字母 s = ord(ch[index].upper()) - ord('A') self.cipher.append(Cipher_list[k, s]) # 输出 for num in self.cipher: ch = chr(num + ord('A')) self.message += ch - 生成加解密表
解密算法
解密没什么好说的,会了加密解密就是减法的过程,因为维吉尼亚就是查表加密的凯撒密码
- 分组打包
- 对应密钥解密
def deCode()
# 分组打包
saveCipher = []
key = 'cipher' #密钥
n = len(key)
tempch = [''] * n
count = 0
for ch in cipher:
if ord('A') <= ord(ch) <= ord('Z') \
or ord('a') <= ord(ch) <= ord('z'):
# 确保了只能是字母才能添加进去
tempch[count % n] = ch
# count计数器,但是为了与分组数一致要%每组字母数
count += 1
if count % n == 0 and count != 0:
saveCipher.append(tempch[0:n + 1]) # 使用切片进行
tempch = [''] * n
if count % n != 0: # 将最后剩下的也打包成一组
saveCipher.append(tempch[0:(count % n)])
# 使用切片将最后一部分单开成一组出来添加
# 解码
deCipher = []
for ch in saveCipher:
for index in range(len(ch)): # 每一组单独解密
# 行不用找,密钥对应每一行,应该在每一行中找对应密文的列,该列就是明文对应的字母数字
for column in range(p): # 找列
if ord(ch[index].upper()) - ord('A') \
== Cipher_list[(ord(key[index].upper())\
- ord('A')), column]:
# print(ch[index].upper(),'key,列:',ord(key[index].upper()) - ord('A'),column)
deCipher.append(column)
break
# 找到了就退出,继续下一下解密字母而不是再继续next密钥,因为一个密钥对应一个字母
# 输出
message = ''
for num in deCipher:
ch = chr(num + ord('A'))
message += ch
print(message)
注意事项
维吉尼亚加密中比较容易犯错的就是没有将明文按照密钥长度进行分小组,然后用key对应着小组的下标进行加密(所以是多表加密,每一个表就是凯撒密码)文章来源:https://www.toymoban.com/news/detail-515497.html
这里我开始有一个误解,就是以为他分好小组之后还需要将其分成每一个组大组然后给每一个密钥的字母进行对应加密,这里我有点过度理解了。到后面真正实现加密解密的时候发现我这里根本就是多此一举,因为我们分号小组之后不可以打乱原本明文或者密文的排序,这里根据密钥长度分小组的意思就是方便我们使用密钥对小组每个字母对应着密钥字母来加密,不然我们也不会说按照密钥长度来分组 ,之后的操作就是双层遍历分好组的列表,然后用每个小组的下标给到对应的秘钥取出来,然后就加密对应的字母即可。文章来源地址https://www.toymoban.com/news/detail-515497.html
到了这里,关于密码学—Vigenere加密Python程序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!