SM2加密算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了SM2加密算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

几何学基础

欧式几何

从一点向另一点可以引一条直线。
任意线段能无限延伸成一条直线。
给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。
所有直角都相等。
若两条直线都与第三条直线相交，并且在同一边的内角之和小于两个直角，则这两条直线在这一边必定相交。

罗巴切夫斯基几何

第五公设不能被证明。
在新的公理体系中展开的一连串推理，得到了一系列在逻辑上无矛盾的新的定理，并形成了新的理论。这个理论像欧氏几何一样是完善的、严密的几何学。

黎曼几何
对于三维空间，有以下三种情形：

曲率恒等于零
曲率为负常数
曲率为正常数

前两种情形分别对应于欧几里得几何学和罗巴切夫斯基几何学，而第三种情形则是黎曼本人的创造，它对应于另一种非欧几何学。黎曼的这第三种几何就是用命题“过直线外一点所作任何直线都与该直线相交”代替第五公设作为前提，保留欧氏几何学的其他公理与公设，经过严密逻辑推理而建立起来的几何体系。这种几何否认“平行线”的存在，是另一种全新的非欧几何，这就是如今狭义意义下的黎曼几何，它是曲率为正常数的几何，也就是普通球面上的几何，又叫球面几何。

椭圆曲线

定义：一条椭圆曲线就是一组被 \(y^2 = x^3 + ax + b\) 定义的且满足 \(4a3+27b2≠0\) 的点集。

椭圆曲线加法（非有限域）：
在椭圆曲线上取一点P(Xp,Yp)，再取一点Q(Xq,Yq)，连接P、Q两点作一条直线，这条直线将在椭圆曲线上交于第三点G，过G点作垂直于X轴的直线，将过椭圆曲线另一点R（一般是关于X轴对称的点），R点则被定义为P+Q的结果，既P+Q=R：
椭圆曲线加法（有限域）：
公式如下
Xr = (λ² - Xp - Xq) mod p
Yr = (λ(Xp - Xr) - Yp) mod p
椭圆曲线乘法：
乘法简化成加法

伽罗瓦域

有限域亦称伽罗瓦域（galois field），是仅含有限个元素的域,它是伽罗瓦(Galois,E.)于18世纪30年代研究代数方程根式求解问题时引出的.有限域的特征数必为某一素数p,因此它含的素域同构于Zp.若F是特征为p的有限域,则F中元素的个数为pⁿ,n为某一正整数.元素个数相同的有限域是同构的.因此,通常用GF(pⁿ)表示pⁿ元的有限域.GF(pⁿ)的乘法群是(pⁿ-1)阶的循环群.

有限域椭圆曲线点的阶

如果椭圆曲线上一点P，存在最小的正整数n使得数乘 \(n P = O ∞ \) ,则将n称为P的阶
若n不存在，则P是无限阶的.

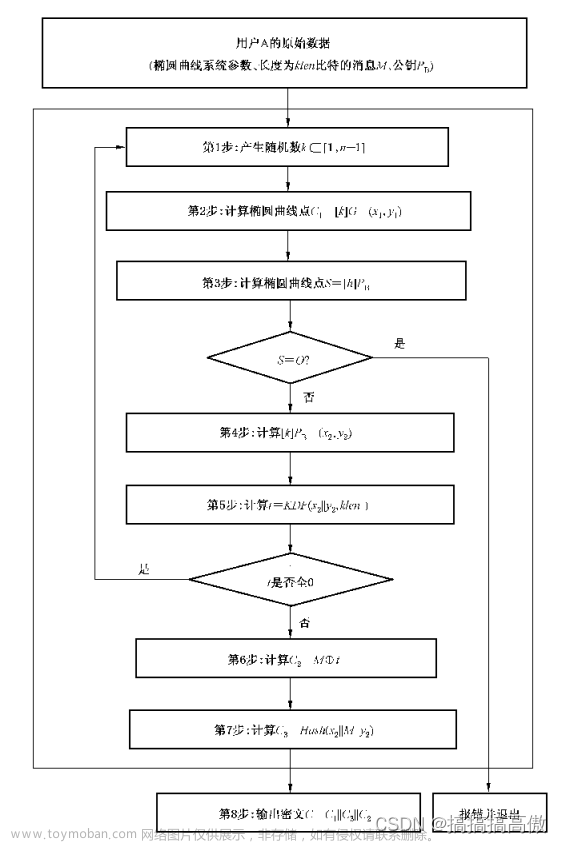
加密原理

考虑 \(K=kG\) ，其中K、G为椭圆曲线Ep(a,b)上的点，n为G的阶（\(nG=O∞ \) ），k为小于n的整数。则给定k和G，根据加法法则，计算K很容易但反过来，给定K和G，求k就非常困难。因为实际使用中的ECC原则上把p取得相当大，n也相当大，要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据。

点G称为基点（base point）
\(k(k<n)\) 为私有密钥（private key）
K为公开密钥（public key)

下面是利用椭圆曲线进行加密通信的过程：
1. 用户A选定一条椭圆曲线Ep(a,b)，并取椭圆曲线上一点，作为基点G。
2. 用户A选择一个私有密钥k，并生成公开密钥K=kG。
3. 用户A将Ep(a,b)和点K，G传给用户B。
4. 用户B接到信息后，将待传输的明文编码到Ep(a,b)上一点M（编码方法很多，这里不作讨论），并产生一个随机整数r（r<n）。
5. 用户B计算点 \(C1 = M + r K \)和\(C2 = M + r K \)。
6. 用户B将 C 1 、 C 2传给用户A。
7. 用户A接到信息后，计算 \(C 1 − k C 2\) ，结果就是点M。再对点M进行解码就可以得到明文。因为\( C 1 − k C 2 = M + r K − k ( r G ) = M + r k G − k r G = M\)