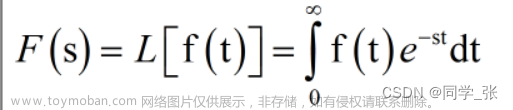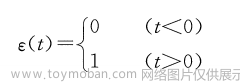概论_第5章_中心极限定理1__定理2(棣莫弗-拉普拉斯中心极限定理)-Toy模板网

这篇具有很好参考价值的文章主要介绍了概论_第5章_中心极限定理1__定理2(棣莫弗-拉普拉斯中心极限定理)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在概率论中，把有关论证随机变量和的极限分布为正态分布的一类定理 $称为中心极限定理$ 。

本文介绍独立同分布序列的中心极限定理。

一独立同分布序列的中心极限定理

定理1 设 $X_1, X_2, ...X_n,...$ 是独立同分布的随机变量序列，且具有相同数学期望和方差， $E(X_i)=\mu, D(X_i)=\sigma^2(i=1,2, ...)$ , 记随机变量 $Y_n=$ $\frac{\sum\limits_{i=1}^{n}X_i-n\mu}{\sqrt{n}\sigma}$ 的分布函数为 $F_n(x)$ , 则对于任意实数 $x$ ,

$\lim\limits_{n \rightarrow \infty}F_n(x) =\lim\limits_{n \rightarrow \infty}P\{Y_n \leqslant x\} =$ $\lim\limits_{n \rightarrow \infty}P$ $\{$ $\frac{\sum\limits_{i=1}^{n}-n\mu}{ \sqrt{n}\sigma}$ $\}$

$=\int_{- \infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt=\Phi(x)$ ,

由这一定理可知以下结论：

1.

当n充分大时，独立同分布的随机变量之和 $Z_n=\sum\limits_{i=1}^{n}X_i$ 的分布近似于正态分布 $N(n\mu, n\sigma^2)$ .
中心极限定理告诉我们，不论 $X_1,X_2, ..., X_n,...$ 同服从什么分布，当n充分大时，其和 $Z_n$ 近似服从正态分布.

2.

考虑独立同分布的随机变量 $X_1, X_2,..., X_n,...$ 的平均值 $\overline X = \frac{1}{n}\sum\limits_{i=1}^{n}X_i$ , 有

E(\overline X) =

\mu

D(\overline X)=

\frac{\sigma^2}{n}

它的标准化随机变量为 $\frac{\overline X - \mu}{\sigma/ \sqrt{n}}$ 即为上述 $Y_n$ , 因此 $\frac{\overline X - \mu}{\sigma/ \sqrt{n}}$ 的分布函数即是上述的 $F_n(x)$ , 因而有

$\lim\limits_{n \rightarrow \infty}F_n(x) =\int_{- \infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt = \Phi(x)$ .

由此可见，当n充分大时，独立同分布随机变量的平均值 $\overline X = \frac{1}{n}\sum\limits_{i=1}^{n}X_i$ 的分布近似于正态分布 $N$ $(\mu, \frac{\sigma^2}{n})$ , 这是独立同分布中心极限定理的另一表达形式。

二棣莫弗—拉普拉斯中心极限定理

此定理是定理1 的特殊情况。

定理2(棣—拉中心极限定理)

设随机变量 $Z_n$ 是n次独立重复试验中事件A发生的次数， p是事件A发生的概率，则对于任意实数 $x$

$\lim\limits_{n \rightarrow \infty}$ P $\{$ $\frac{Z_n-np}{\sqrt{np(1-p)}}\leqslant x$ $\}$ $=\int_{- \infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt = \Phi(x)$ .

由棣—拉中心极限定理，得到下列结论：

1.

在贝努利试验中，若事件A发生的概率为p, 设 $Z_n$ 为n次独立重复试验中事件A发生的频数，则当n充分大时， $Z_n$ 近似服从 $N (n p, n p (1 - p))$ .

2.

在贝努利试验中，若事件A发生的概率为p, $\frac{Z_n}{n}$ 为n次独立重复试验中事件A 发生的频率，则当n充分大时， $\frac{Z_n}{n}$ 近似服从 $\frac{p(1-p)}{n})$ .

文章来源地址https://www.toymoban.com/news/detail-516342.html

三例题

设随机变量X~B（100， 0.2）, $\Phi(x)$ 为标准正态分布函数，已知 $\Phi(2.5)=0.9938$ , 应用中心极限定理，可得 P{ $20\leqslant x \leqslant 30$ } $\approx$ ___________。

解： X ~ B(100, 0.2), np=20, npq = 16, 则P{20 $\leqslant x \leqslant 30$ } = $P\{{\frac{20-20}{\sqrt{16}} \leqslant \frac{X-20}{\sqrt{16}} \leqslant \frac{30-20}{\sqrt{16}}}\}$ (这一步用到定理2)
$\approx \Phi(\frac{30-20}{4}) - \Phi(\frac{20-20}{4}) = \Phi(2.5) - \Phi(0) = 0.9938-0.5 = 0.4938$ .
答案为 0.4938。