c++红与黑（DFS之连通性模型）-Toy模板网

这篇具有很好参考价值的文章主要介绍了c++红与黑（DFS之连通性模型）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

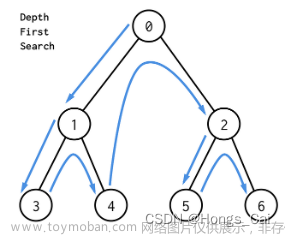
连通性是图论中一个重要的概念，用于描述图中的点与点之间是否存在路径。在连通图中，任意两个点之间都存在至少一条路径。而在非连通图中，存在一些点与其它点没有连通的路径。

在使用深度优先搜索（DFS）算法解决图论问题中，连通性模型是一个经典且重要的应用场景。简单来说，连通性模型就是通过 DFS 算法判定一幅图是否是连通图。具体实现过程中，我们可以从一个起点开始遍历整个图，标记遍历到的节点为已访问，若最终遍历到的节点数量等于图中节点总数，则说明整个图是连通的；反之，如果存在未遍历到的节点，则说明图是非连通的。

通过连通性模型，我们可以解决一些和图连通性有关的问题，例如：

- 问一个图是否是连通图；
- 求一个图中有多少个连通分量；
- 求一个图中任意两个点之间的距离。

这些问题都可以通过 DFS 算法来解决，其中连通性模型是基础且重要的部分，因此深入掌握该模型对于理解和解决图论问题非常有帮助。

先看题目：

有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。

你站在其中一块黑色的瓷砖上，只能向相邻（上下左右四个方向）的黑色瓷砖移动。

请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

输入格式
输入包括多个数据集合。

每个数据集合的第一行是两个整数 W 和 H，分别表示 x 方向和 y 方向瓷砖的数量。

在接下来的 H 行中，每行包括 W 个字符。每个字符表示一块瓷砖的颜色，规则如下

1）‘.’：黑色的瓷砖；
2）‘#’：红色的瓷砖；
3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。

当在一行中读入的是两个零时，表示输入结束。

输出格式
对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

数据范围
1≤W,H≤20

输入数据：

6 9 
....#. 
.....# 
...... 
...... 
...... 
...... 
...... 
#@...# 
.#..#. 
0 0

输出数据

注意：其实这题也可以用bfs做，但是可以用dfs，代码量可以减少，更方便理解和解题，所以我们在既可以用dfs，也可以用bfs，一般选择dfs

老规矩，先看代码

#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 25;

int n, m;
char g[N][N];
bool st[N][N];

int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};

int dfs(int x, int y)
{
    int cnt = 1;
    
    st[x][y] = true;

    for(int i = 0; i < 4; i ++ )
    {
        int a = x + dx[i], b = y + dy[i];
        
        if(a < 0 || a >=n || b < 0 || b >= m) continue;
        if(st[a][b]) continue;
        if(g[a][b] != '.') continue;
        
        cnt += dfs(a, b);
    }
    
    return cnt;
}

int main()
{
    while(cin >> m >> n, m || n)
    {
        for(int i = 0; i < n; i ++ ) cin >> g[i];
    
        int x, y;
        for(int i = 0; i < n; i ++ )
        {
            for(int j = 0; j < m; j ++ )
            {
                if(g[i][j] == '@')
                {
                    x = i;
                    y = j;
                }
            }
        }
        
        memset(st, 0, sizeof st);
        
        cout<< dfs(x, y) << endl;
    }
    
    return 0;
}

1、注意输出格式，在输入两个0的时候结束

2、g[N][N]存储图，st[N]代表判断当前某个点有没有被使用过

3、判断开始的条件，并且每一遍都要初始化st数组，因为换数据的时候每一个点都是没有被使用过的

4、使用cnt来存储总数，标记当前点，已经被使用过了

5、使用偏移量来让当前点移动，而且点的移动一般都是从最外圈开始，慢慢到最内圈，类似于蛇形矩阵

6、出界和当前点被使用过了就重新开始，不然的话cnt++，继续深搜，然后回溯，返回cnt

理解的小伙伴麻烦点个赞吧文章来源地址https://www.toymoban.com/news/detail-516999.html

到了这里，关于c++红与黑（DFS之连通性模型）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！