1.背景介绍
樽海鞘,身体呈透明的桶状。它们的组织与水母非常相似。它们的运动也非常类似于水母,在水母中,水被泵送通过身体作为推进向前运动。输卵管的形状如图1(a)所示。

关于这种生物的生物学研究处于早期阶段,主要是因为它们的生活环境极难进入,而且很难将它们保存在实验室环境中。樽海鞘最有趣的行为之一,也是论文中感兴趣的,是它们的群集行为。在深海中,沙鱼经常形成一个称为沙鱼链的群体。该链条如图1(b)所示。这种行为的主要原因尚不清楚,但一些研究人员认为,这样做是为了通过快速协调的变化和觅食来实现更好的运动。
2.数学模型
2.1 提出的移动樽海鞘链的数学模型
为了对樽海鞘(salp)链进行数学建模,首先将种群分为两组:领导者和追随者。领导者是链前面的salp,而salp的其余部分则被视为追随者。正如这些salps的名字所暗示的那样,领导者引导群体,追随者相互跟随(以及领导者直接或间接)。
类似于其他基于群的技术,salps的位置是在n维搜索空间中定义的,其中n是给定问题的变量数。因此,所有salps的位置都存储在一个称为x的二维矩阵中。还假设在搜索空间中有一个名为F的食物源作为群体的目标。
为了更新领导者的位置,提出了以下等式:

其中,x1j表示第一个salp(前导)在第j维中的位置,Fj是食物源在第j维度中的位置、ubj表示第j维的上界、lbj表示第i维的下界,c1、c2和c3是随机数。
等式(3.1)表明,引导器仅更新其相对于食物源的位置。系数c1是SSA中最重要的参数,因为它平衡了勘探和开采,定义如下:

其中l是当前迭代,l是迭代的最大次数。
参数c2和c3是在[0,1]的区间中均匀生成的随机数。事实上,它们决定了第j维中的下一个位置是朝向正无穷大还是负无穷大,以及步长。
为了更新从动件的位置,使用以下方程(牛顿运动定律):

当i≥2时,xi j表示第i个跟随器salp在j维的位置,t是时间,v0是初始速度,a=v_final/v_0,其中v=(x−x_0)/t。
因为优化中的时间是迭代,所以迭代之间的差异等于1,并且考虑v0=0,这个方程可以表示如下:

其中i≥2,xi j表示第i个跟随器salp在j维中的位置。
利用等式(3.1)和(3.4),可以模拟salp链。
2.2 Swarm仿真
为了观察上述数学模型的效果,在本小节中进行了模拟。二十条salps被随机放置在有固定或移动食物来源的搜索空间中。输卵管链的位置和每条输卵管的历史如图2-5所示。请注意,图中的蓝色点表示食物来源的位置,最深的圆圈是最前面的salp。跟随者的萨尔普根据其在萨尔普链中相对于引导者的位置而被涂上灰色。在图2和图4中检查salp链在九次连续迭代中的行为,可以观察到,在第一次迭代后,可以使用有效提出的方程形成和移动群。此外,可以看出,在迭代过程中,领先的salp会改变其在食物来源周围的位置,而跟随的salp则会逐渐跟随它。两个模拟都使用了相同的模型,并且在两个2D中都使用了该模型的优点
图3和图5显示了100次迭代后,在2D和3D空间中固定和移动食物源周围的salp的位置历史。在固定食物源周围搜索的点表明,salp在搜索空间周围有效地移动。点的分布是合理的,表明所提出的模型能够探索和利用固定食物源周围的空间。此外,图3和图5显示,所提出的数学模型要求salp链中的salp追逐移动的食物源。在起点周围搜索的点的分布高于终点。这是由于控制勘探和开发的c1参数。这些发现证明,salp链运动模型能够探索和利用固定和移动食物来源周围的空间。




2.3 单目标Salp Swarm算法(SSA)
不用说,模拟salp链的数学模型不能直接用于解决优化问题。换句话说,需要稍微调整一下模型,使其适用于优化问题。单目标优化器的最终目标是确定全局最优。在SSA群模型中,跟随salp跟随前导salp。主要的沙拉酱也向食物来源移动。因此,如果食物源被全局最优替代,salp链会自动向其移动。然而,问题是优化问题的全局最优是未知的。在这种情况下,假设到目前为止获得的最佳解决方案是全局最优的,并假设为salp链追逐的食物来源。
SSA算法的伪代码如图6.1所示。该图显示SSA算法通过启动具有随机位置的多个salp来开始逼近全局最优。然后,它计算每个salp的适应度,找到适应度最好的salp,并将最佳salp的位置分配给变量F,作为salp链要追逐的源食物。同时,使用等式(3.2)更新系数c1。对于每个维度,使用等式(3.1)来更新前导salp的位置和使用等式(3.4)来更新跟随salp的地位。如果任何salp超出搜索空间,它将被带回到边界上。除了初始化之外的所有上述步骤都被反复执行,直到满足结束标准为止。
3.算法流程图

4.文件结构

func_plot.m % 绘制的基准函数
Get_Functions_details.m % 基准的全部信息和实现
initialization.m % 初始化
main.m % 主函数
SSA.m % 樽海鞘群优化算法
5.伪代码

6.详细代码及注释
6.1 func_plot.m
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
end
6.2 Get_Functions_details.m
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=30;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=10;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=10;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=10;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=10;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=10;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=10;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=10;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=10;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=10;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=10;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=10;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=10;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
6.3 initialization.m
function Positions=initialization(SearchAgents_no,dim,ub,lb)
Boundary_no= size(ub,1); % numnber of boundaries
% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1
Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end
% If each variable has a different lb and ub
if Boundary_no>1
for i=1:dim
ub_i=ub(i);
lb_i=lb(i);
Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end
end
6.4 main.m
clear all
clc
SearchAgents_no=30; % Number of search agents
Function_name='F1'; % Name of the test function that can be from F1 to F23 (
Max_iteration=1000; % Maximum numbef of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,SSA_cg_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
figure('Position',[500 500 660 290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
%Draw objective space
subplot(1,2,2);
semilogy(SSA_cg_curve,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
box on
legend('SSA')
display(['The best solution obtained by SSA is \m ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by SSA is \n ', num2str(Best_score)]);
6.5 SSA.m
function [FoodFitness,FoodPosition,Convergence_curve]=SSA(N,Max_iter,lb,ub,dim,fobj)
if size(ub,1)==1
ub=ones(dim,1)*ub;
lb=ones(dim,1)*lb;
end
Convergence_curve = zeros(1,Max_iter);
%Initialize the positions of salps
SalpPositions=initialization(N,dim,ub,lb);
FoodPosition=zeros(1,dim);
FoodFitness=inf;
%calculate the fitness of initial salps
for i=1:size(SalpPositions,1)
SalpFitness(1,i)=fobj(SalpPositions(i,:));
end
[sorted_salps_fitness,sorted_indexes]=sort(SalpFitness);
for newindex=1:N
Sorted_salps(newindex,:)=SalpPositions(sorted_indexes(newindex),:);
end
FoodPosition=Sorted_salps(1,:);
FoodFitness=sorted_salps_fitness(1);
%Main loop
l=2; % start from the second iteration since the first iteration was dedicated to calculating the fitness of salps
while l<Max_iter+1
c1 = 2*exp(-(4*l/Max_iter)^2); % Eq. (3.2) in the paper
for i=1:size(SalpPositions,1)
SalpPositions= SalpPositions';
if i<=N/2
for j=1:1:dim
c2=rand();
c3=rand();
%%%%%%%%%%%%% % Eq. (3.1) in the paper %%%%%%%%%%%%%%
if c3<0.5
SalpPositions(j,i)=FoodPosition(j)+c1*((ub(j)-lb(j))*c2+lb(j));
else
SalpPositions(j,i)=FoodPosition(j)-c1*((ub(j)-lb(j))*c2+lb(j));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end
elseif i>N/2 && i<N+1
point1=SalpPositions(:,i-1);
point2=SalpPositions(:,i);
SalpPositions(:,i)=(point2+point1)/2; % % Eq. (3.4) in the paper
end
SalpPositions= SalpPositions';
end
for i=1:size(SalpPositions,1)
Tp=SalpPositions(i,:)>ub';Tm=SalpPositions(i,:)<lb';SalpPositions(i,:)=(SalpPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;
SalpFitness(1,i)=fobj(SalpPositions(i,:));
if SalpFitness(1,i)<FoodFitness
FoodPosition=SalpPositions(i,:);
FoodFitness=SalpFitness(1,i);
end
end
Convergence_curve(l)=FoodFitness;
l = l + 1;
end
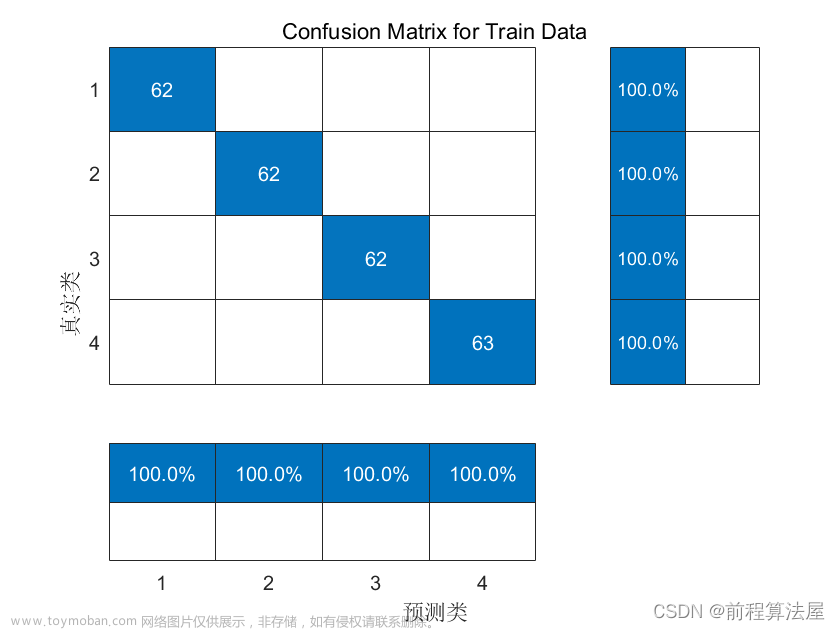
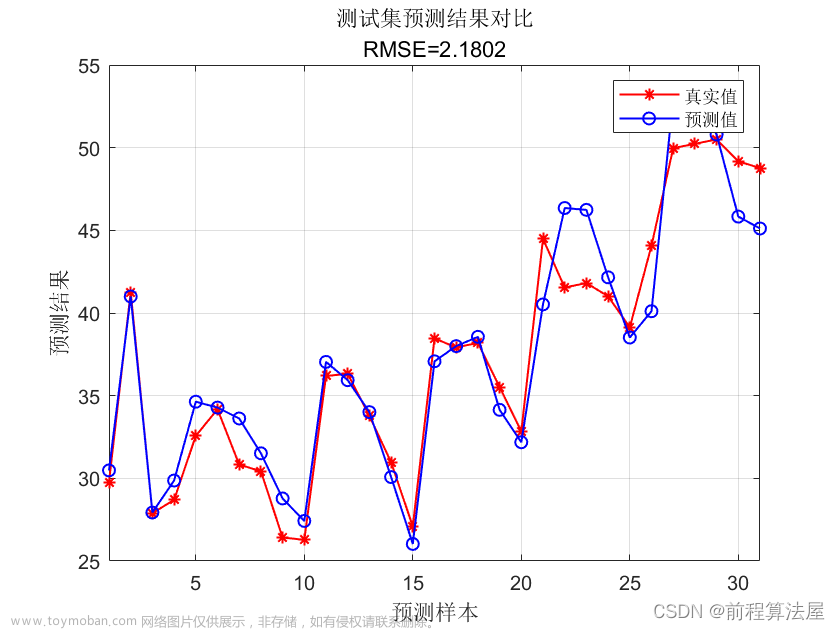
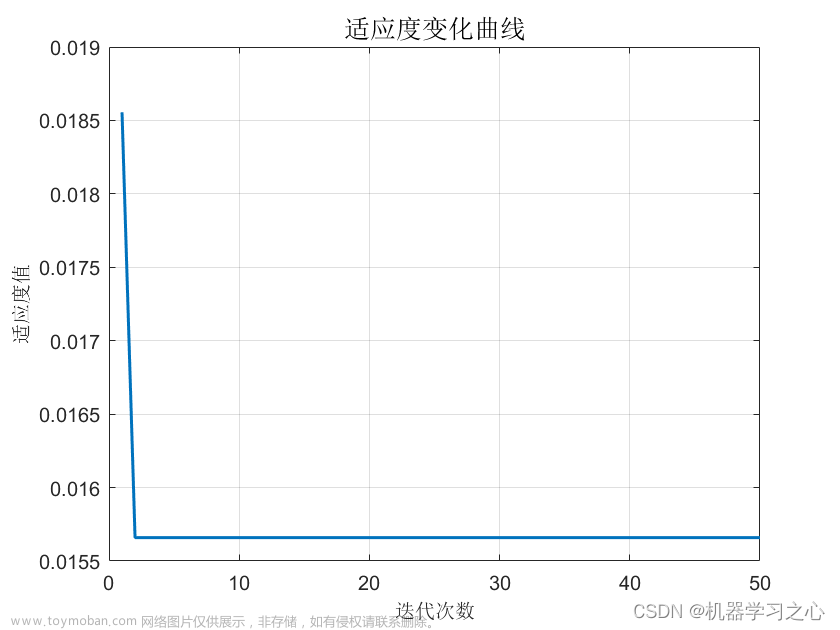
7.运行结果
 文章来源:https://www.toymoban.com/news/detail-518160.html
文章来源:https://www.toymoban.com/news/detail-518160.html
8.参考文献
[1]Mirjalili S,Gandomi H A,Mirjalili Z S, et al. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software,2017,114.文章来源地址https://www.toymoban.com/news/detail-518160.html
到了这里,关于【Matlab】智能优化算法_樽海鞘群算法SSA的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!