前置知识:黎曼积分的概念
介绍
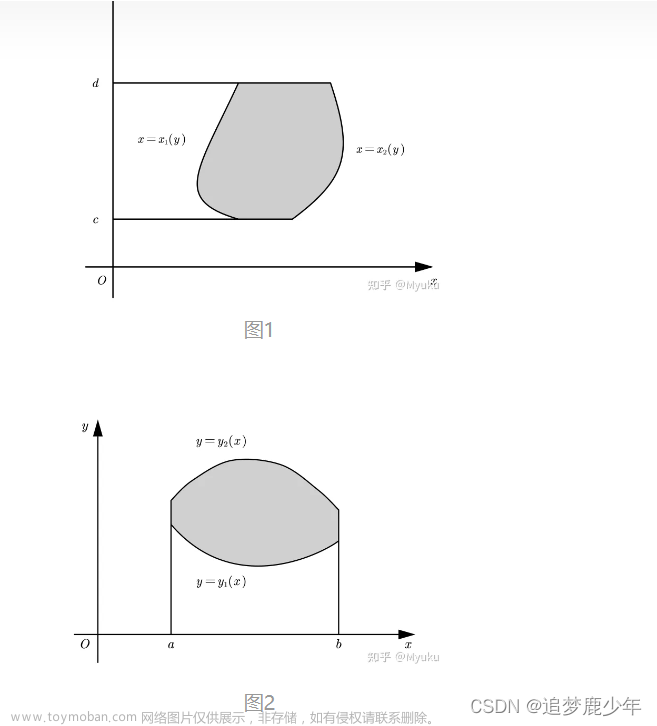
由前置知识可得,黎曼积分可以求 x = a x=a x=a, x = b x=b x=b, x x x轴和 y = f ( x ) y=f(x) y=f(x)围成的图形,
S = ∫ a b f ( x ) d x S=\int_a^bf(x)dx S=∫abf(x)dx
那么,我们就可以用这个方法来求平面区域的面积。
例题
设平面区域 D D D由曲线 y = x 2 y=x^2 y=x2和 x = y 2 x=y^2 x=y2围成,求 D D D的面积 S S S
解:
\qquad
两曲线的交点为点
(
0
,
0
)
(0,0)
(0,0)和点
(
1
,
1
)
(1,1)
(1,1),由此可得
S = ∫ 0 1 x d x − ∫ 0 1 x 2 d x \qquad S=\int_0^1\sqrt xdx-\int_0^1x^2dx S=∫01xdx−∫01x2dx
= ∫ 0 1 ( x − x 2 ) d x \qquad\quad =\int_0^1(\sqrt x-x^2)dx =∫01(x−x2)dx
= ( 2 3 x 3 2 − 1 3 x 3 ) ∣ 0 1 \qquad\quad =(\dfrac 23x^{\frac 32}-\dfrac 13x^3)\bigg\vert_0^1 =(32x23−31x3) 01文章来源:https://www.toymoban.com/news/detail-518573.html
= 1 3 \qquad\quad =\dfrac 13 =31文章来源地址https://www.toymoban.com/news/detail-518573.html
到了这里,关于定积分求平面区域的面积的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!