最小生成树算法之Kruskal算法（c++）-Toy模板网

这篇具有很好参考价值的文章主要介绍了最小生成树算法之Kruskal算法（c++）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

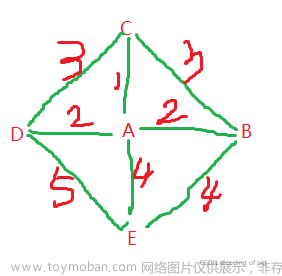
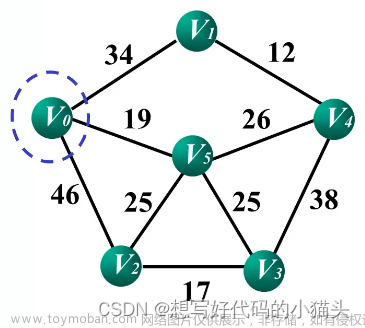
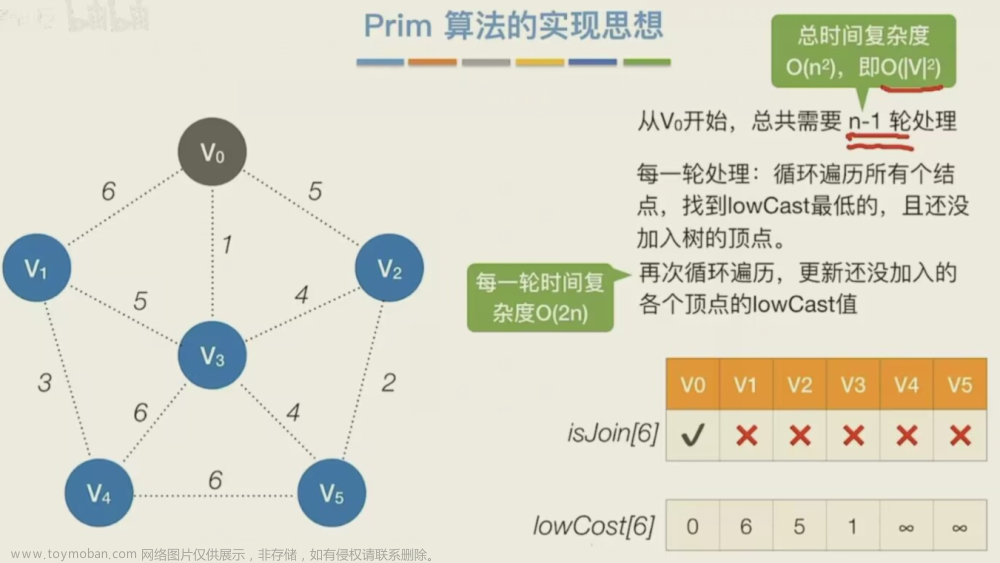
与Prim算法生成图的最小生成的树算法不同在于：

Prim算法是基于图中的顶点的，且不依赖于边，Prim从顶点出发拓展，依次找每个顶点相邻的权值最小的边，直至生成最小生成树。因此，Prim算法的时间复杂度是O(v^2),适合边稠密图。

而Kruskal算法恰恰相反，是基于图中的边的一种算法，Kruskal算法的思想是：

从图中所有的边中依次选出权值最小的边，同时选出边两端的顶点，直至构成一个最小生成树。使用这种思想构建最小生成树，就会用到并查集判断当前的边时候还能添加进最小生成树。

Kruskal的算法核心代码：

void Kruskal(road *R, int* v, int n) {
	int a, b;
	int sum = 0;
	for (int i = 0; i < n; i++)
	{
		a = GetRoad(v,R[i].begin);
		b = GetRoad(v,R[i].end);
		if (a != b)
		{
			v[a] = b;
			sum += R[i].weight;
		}
	}
	cout << endl << sum;
}

并查集的算法核心代码：

int GetRoad(int *v, int p) {
	while (p != v[p])
	{
		p = v[p];
	}
	return p;
}

完整代码：

#include<iostream>
using namespace std;
#define MAX 4
typedef struct EdgeNode {
	int adjvex;
	int weight;
	EdgeNode* next;
};
typedef struct VexNode {
	char data;
	EdgeNode* first;
};
typedef struct Graph {
	VexNode GraphList[MAX];
	int vexnum;
	int edgenum;
};
typedef struct road {
	int begin;
	int end;
	int weight;
};
void CreatGraph(Graph &G) {
	int i, j, w;
	EdgeNode* e = NULL;
	EdgeNode* q = NULL;
	cout << "请输入顶点数和变数： " << endl;
	cin >> G.vexnum >> G.edgenum;
	cout << "请输入顶点信息: " << endl;
	for (int k = 0; k < G.vexnum; k++)
	{
		cin >> G.GraphList[k].data;
		G.GraphList[k].first = NULL;
	}
	for (int k = 0; k < G.edgenum; k++)
	{
		cout << "请输入边(vi,vj)的下标i,j以及权值： " << endl;
		cin >> i >> j >> w;
		e = new EdgeNode;
		e->weight = w;
		e->adjvex = j;
		e->next = G.GraphList[i].first;
		G.GraphList[i].first = e;
		/*q = new EdgeNode;
		q->weight = w;
		q->adjvex = i;
		q->next = G.GraphList[j].first;
		G.GraphList[j].first = q;*/
	}
}
void myprint(Graph G) {
	cout << "输入的邻接表图如下：" << endl;
	EdgeNode* p;
	for (int i = 0; i < G.vexnum; i++)
	{
		cout << G.GraphList[i].data << " ";
		for (p = G.GraphList[i].first; p; p = p->next)
		{
			cout << p->adjvex << " ";
		}
		cout << endl;
	}
}
void Sort(road* R,int n)
{
	int temp,tbe,ten;
	int min = R[0].weight;
	int flag = 0;
	int i, j;
	for ( i = 1; i < n; i++)
	{
		if (R[i].weight < R[i - 1].weight)
		{
			temp = R[i].weight;
			tbe = R[i].begin;
			ten = R[i].end;
			for (j = i - 1; temp < R[j].weight; j--)
			{
				R[j + 1].weight = R[j].weight;
				R[j + 1].begin = R[j].begin;
				R[j + 1].end = R[j].end;
			}
			R[j + 1].weight = temp;
			R[j + 1].begin = tbe;
			R[j + 1].end = ten;
		}
	}
}
void creatRoad(Graph G, road* R) {
	int j = 0;
	for (int i = 0; i < G.vexnum; i++)
	{
		EdgeNode* p = NULL;
		for (p = G.GraphList[i].first; p; p = p->next)
		{
			R[j].begin = i;
			R[j].end = p->adjvex;
			R[j].weight = p->weight;
			j++;
		}
	}
}
int GetRoad(int *v, int p) {
	while (p != v[p])
	{
		p = v[p];
	}
	return p;
}
void Kruskal(road *R, int* v, int n) {
	int a, b;
	int sum = 0;
	for (int i = 0; i < n; i++)
	{
		a = GetRoad(v,R[i].begin);
		b = GetRoad(v,R[i].end);
		if (a != b)
		{
			v[a] = b;
			sum += R[i].weight;
		}
	}
	cout << endl << sum;
}
int main() {
	int v[MAX];
	for (int i = 0; i < MAX; i++)
	{
		v[i] = i;
	}
	Graph G;
	CreatGraph(G);
	road R[100];
	//myprint(G);
	creatRoad(G, R);
	Sort(R, G.edgenum);
	cout << "Kruskal：" << endl;
	Kruskal(R, v, G.edgenum);
	return 0;
}

执行结果：

我构建的图：

kruskal算法c++程序,数据结构,算法,c++,图论,数据结构