在上一节的内容中,我们介绍了UKF中最重要的内容—无迹变换UT,今天我们将具体介绍UKF是如何实现的。
好了,话不多说,开整!!!
UKF算法的实现
我们知道,我们可以使用状态方程和观测方程来对系统进行描述,那么一个非线性系统可以用以下的方程进行描述:
{
X
(
k
+
1
)
=
f
(
x
(
k
)
,
V
(
k
)
)
Z
(
k
)
=
h
(
x
(
k
)
,
W
(
k
)
)
\left\{\begin{array}{l}X\left(k+1\right)=f\left(x\left(k\right),V\left(k\right)\right)\\ Z\left(k\right)=h\left(x\left(k\right),W\left(k\right)\right)\end{array}\right.
{X(k+1)=f(x(k),V(k))Z(k)=h(x(k),W(k))
其中的
- f f f为非线性状态方程函数
- V ( k ) V(k) V(k)为过程噪声,其协方差矩阵为Q
- h h h为非线性观测方程函数
- W ( k ) W(k) W(k)为量测噪声,协方差矩阵为R
在描述完非线性系统后,对不同时刻的数据进行滤波,步骤如下:
-
1、首先
获得一组Sigma点集(采样点集)与权值,计算如下式:

详细介绍请见:
UKF在目标跟踪中的应用(一)
也即:
X ( i ) ( k ∣ k ) = [ X ^ ( k ∣ k ) X ^ ( k ∣ k ) + ( n + λ ) P ( k ∣ k ) X ^ ( k ∣ k ) − ( n + λ ) P ( k ∣ k ) ] X^{(i)}(k|k)=[\hat{X}(k|k)\quad\hat{X}(k|k)+\sqrt{(n+\lambda)P(k|k)}\quad\hat{X}(k|k)-\sqrt{(n+\lambda)P(k|k)}] X(i)(k∣k)=[X^(k∣k)X^(k∣k)+(n+λ)P(k∣k)X^(k∣k)−(n+λ)P(k∣k)] -
2、然后
计算2n+1个Sigma点的一步预测值,i=1,2……2n+1;
X ( i ) ( k + 1 ∣ k ) = f [ k , X ( i ) ( k ∣ k ) ] X^{(i)}(k+1|k)=f[k,X^{(i)}(k|k)] X(i)(k+1∣k)=f[k,X(i)(k∣k)] -
3、
计算系统状态量和协方差矩阵的一步预测值
X
^
(
k
+
1
∣
k
)
=
∑
i
=
0
2
n
ω
(
i
)
X
(
i
)
(
k
+
1
∣
k
)
\hat{X}(k+1|k)=\sum_{i=0}^{2n}\omega^{(i)}X^{(i)}(k+1|k)
X^(k+1∣k)=i=0∑2nω(i)X(i)(k+1∣k)
P
(
k
+
1
∣
k
)
=
∑
k
=
0
2
n
ω
(
k
)
[
X
^
(
k
+
1
∣
k
)
−
X
(
k
)
(
k
+
1
∣
k
)
]
[
X
^
(
k
+
1
∣
k
)
−
X
(
n
)
(
k
+
1
∣
k
)
]
T
+
Q
P(k+1|k)=\sum\limits_{k=0}^{2n}\omega^{(k)}[\hat{X}(k+1|k)-X^{(k)}(k+1|k)][\hat{X}(k+1|k)-X^{(n)}(k+1|k)]^T+Q
P(k+1∣k)=k=0∑2nω(k)[X^(k+1∣k)−X(k)(k+1∣k)][X^(k+1∣k)−X(n)(k+1∣k)]T+Q
此处就与Kalman明显不同:
在Kalman滤波中,只需将上一时刻的值带入状态方程计算一次即可得到预测值,UKF是将一组采样点值进行预测,然后加权,得到状态的预测值
-
4、再根据一步预测值,使用
UT变换,产生新的Sigma点集,
X ( i ) ( k + 1 ∣ k ) = [ X ^ ( k + 1 ∣ k ) X ^ ( k + 1 ∣ k ) + ( n + λ ) P ( k + 1 ∣ k ) X ^ ( k + 1 ∣ k ) − ( n + λ ) P ( k + 1 ∣ k ) ] X^{(i)}(k+1|k)=[\hat{X}(k+1|k) \quad \hat{X}(k+1|k)+\sqrt{(n+\lambda)P(k+1|k)} \quad \hat{X}(k+1|k)-\sqrt{(n+\lambda)P(k+1|k)}] X(i)(k+1∣k)=[X^(k+1∣k)X^(k+1∣k)+(n+λ)P(k+1∣k)X^(k+1∣k)−(n+λ)P(k+1∣k)] -
5、将步骤4中
新产生的Sigma点集带入观测方程,得到观测的预测值,i=1,2,……2n+1;
Z ( i ) ( k + 1 ∣ k ) = h [ X ( i ) ( k + 1 ∣ k ) ] Z^{(i)}\left(k+1|k\right)=h[X^{(i)}(k+1|k)] Z(i)(k+1∣k)=h[X(i)(k+1∣k)] -
6、通过步骤5中得到的
Sigma点集的观测预测值,加权求和得到系统预测的均值和方差,
Z ‾ ( k + 1 ∣ k ) = ∑ i = 0 2 n ω ( i ) Z ( i ) ( k + 1 ∣ k ) \overline{Z}(k+1|k)=\sum\limits_{i=0}^{2n}\omega^{(i)}{Z}^{(i)}(k+1|k) Z(k+1∣k)=i=0∑2nω(i)Z(i)(k+1∣k)
P z k z k = ∑ i = 0 2 n ω ( i ) [ Z ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] [ Z ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] T + R P_{z_kz_k}=\sum\limits_{i=0}^{2n}\omega^{(i)}[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)][Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]^{\mathrm{T}}+R Pzkzk=i=0∑2nω(i)[Z(i)(k+1∣k)−Z(k+1∣k)][Z(i)(k+1∣k)−Z(k+1∣k)]T+R
P x k z k = ∑ i = 0 2 π ω ( i ) [ X ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] [ Z ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] T P_{x_k z_k}=\sum\limits_{i=0}^{2\pi}\omega^{(i)}[X^{(i)}(k+1|k)-\overline{Z}(k+1|k)][Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]^T Pxkzk=i=0∑2πω(i)[X(i)(k+1∣k)−Z(k+1∣k)][Z(i)(k+1∣k)−Z(k+1∣k)]T -
7、
计算滤波增益K
K ( k + 1 ) = P x k z k P z k z k − 1 K(k+1)=P_{x_k z_k}P_{z_k z_k}^{-1} K(k+1)=PxkzkPzkzk−1 -
8、状态更新、协方差更新:
X ^ ( k + 1 ∣ k + 1 ) = X ^ ( k + 1 ∣ k ) + K ( k + 1 ) [ Z ( k + 1 ) − Z ^ ( k + 1 ∣ k ) ] \hat{X}\left(k+1|k+1\right)=\hat{X}\left(k+1|k\right)+K\left(k+1\right)\left[Z\left(k+1\right)-\hat{Z}\left(k+1|k\right)\right] X^(k+1∣k+1)=X^(k+1∣k)+K(k+1)[Z(k+1)−Z^(k+1∣k)]
P ( k + 1 ∣ k + 1 ) = P ( k + 1 ∣ k ) − K ( k + 1 ) P z k z k K ⊺ ( k + 1 ) P(k+1|k+1)=P(k+1|k)-K(k+1)P_{z_kz_k}K^{\intercal}(k+1) P(k+1∣k+1)=P(k+1∣k)−K(k+1)PzkzkK⊺(k+1)
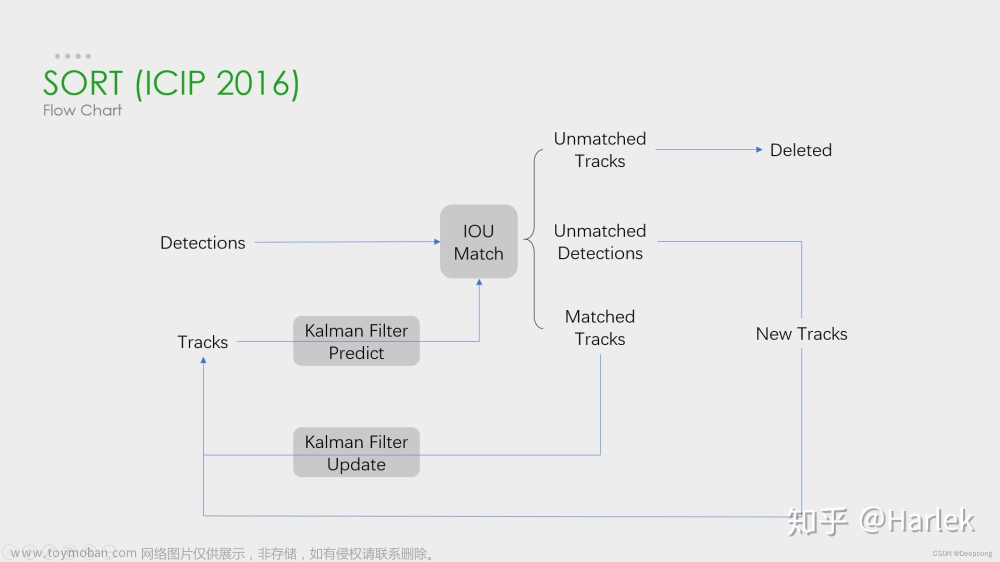
经过上述的步骤,即可完成一次滤波,然后不断循环进行即可,如果用一张图表示UKF滤波过程,可以如下图所示:
下次将对其进行MATLAB仿真验证。文章来源:https://www.toymoban.com/news/detail-520204.html
上述内容即使今天的全部内容了,感谢大家的观看。
如果方便,辛苦大家点个赞和关注哦!
您的点赞或评论或关注是对我最大的肯定,谢谢大家!!!文章来源地址https://www.toymoban.com/news/detail-520204.html
到了这里,关于无迹卡尔曼滤波在目标跟踪中的作用(二)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!