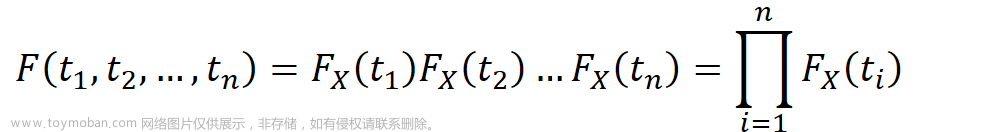涉及到样本方差的计算的时候,一般题中会给很多数据,用定义式计算会很麻烦,整理了两个常用计算式,以及回归问题涉及到求
S
x
x
S_{xx}
Sxx,
S
x
y
S_{xy}
Sxy,
S
y
y
S_{yy}
Syy的总结定义式
s
2
=
1
n
−
1
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
s^2=\frac{1}{n-1} \sum_{i=1}^{n} (x_{i}-\bar{x})^2
s2=n−11∑i=1n(xi−xˉ)2,其中
x
ˉ
\bar{x}
xˉ为样本均值
计算式1——已知:样本值平方和&样本均值
s
2
=
1
n
−
1
∑
i
=
1
n
x
i
2
−
n
x
ˉ
2
s^2=\frac{1}{n-1} \sum_{i=1}^{n}x_{i}^2-n\bar{x}^2
s2=n−11i=1∑nxi2−nxˉ2
计算式2——已知:样本值平方和&样本值的和
s
2
=
1
n
(
n
−
1
)
[
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
]
s^2=\frac{1}{n(n-1)} [n\sum_{i=1}^{n} x_{i}^2-(\sum_{i=1}^{n} x_{i})^2]
s2=n(n−1)1[ni=1∑nxi2−(i=1∑nxi)2]推导:文章来源:https://www.toymoban.com/news/detail-520547.html
s
2
=
1
n
−
1
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
=
1
n
−
1
∑
i
=
1
n
(
x
i
2
−
2
x
ˉ
x
i
+
x
ˉ
2
)
=
1
n
−
1
(
∑
i
=
1
n
x
i
2
−
2
x
ˉ
∑
i
=
1
n
x
i
+
∑
i
=
1
n
x
ˉ
2
)
=
1
n
−
1
(
∑
i
=
1
n
x
i
2
−
2
n
x
ˉ
2
+
n
x
ˉ
2
)
=
1
n
−
1
(
∑
i
=
1
n
x
i
2
−
n
x
ˉ
2
)
=
1
n
(
n
−
1
)
(
n
∑
i
=
1
n
x
i
2
−
n
2
x
ˉ
2
)
=
1
n
(
n
−
1
)
[
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
]
\begin{aligned} s^2 &= \frac{1}{n-1} \sum_{i=1}^{n} (x_{i}-\bar{x})^2 \\ &= \frac{1}{n-1} \sum_{i=1}^{n}(x_{i}^2-2\bar{x}x_{i}+\bar{x}^2) \\ &= \frac{1}{n-1} (\sum_{i=1}^{n}x_{i}^2-2\bar{x}\sum_{i=1}^{n}x_{i}+\sum_{i=1}^{n}\bar{x}^2)\\ &= \frac{1}{n-1} (\sum_{i=1}^{n}x_{i}^2-2n\bar{x}^2+n\bar{x}^2)\\ &= {\color{Red} \frac{1}{n-1} (\sum_{i=1}^{n}x_{i}^2-n\bar{x}^2)} \\ &= \frac{1}{n(n-1)} (n\sum_{i=1}^{n}x_{i}^2-n^2\bar{x}^2) \\ &= {\color{Red} \frac{1}{n(n-1)} [n\sum_{i=1}^{n}x_{i}^2-(\sum_{i=1}^{n}x_{i})^2]} \\ \end{aligned}
s2=n−11i=1∑n(xi−xˉ)2=n−11i=1∑n(xi2−2xˉxi+xˉ2)=n−11(i=1∑nxi2−2xˉi=1∑nxi+i=1∑nxˉ2)=n−11(i=1∑nxi2−2nxˉ2+nxˉ2)=n−11(i=1∑nxi2−nxˉ2)=n(n−1)1(ni=1∑nxi2−n2xˉ2)=n(n−1)1[ni=1∑nxi2−(i=1∑nxi)2]回归应用
S
x
x
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
=
∑
i
=
1
n
(
x
i
2
)
−
(
∑
i
=
1
n
x
i
)
2
n
(由计算式2推出)
S_{x x}=\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}= \sum_{i=1}^{n}(x_{i}^2)-\frac{{\color{Red}(\sum_{i=1}^{n}x_{i})^2}}{n} \tag{由计算式2推出}
Sxx=i=1∑n(xi−xˉ)2=i=1∑n(xi2)−n(∑i=1nxi)2(由计算式2推出)
S
y
y
=
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
=
∑
i
=
1
n
(
y
i
2
)
−
(
∑
i
=
1
n
y
i
)
2
n
S_{yy}=\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}= \sum_{i=1}^{n}(y_{i}^2)-\frac{{\color{Red}(\sum_{i=1}^{n}y_{i})^2}}{n}
Syy=i=1∑n(yi−yˉ)2=i=1∑n(yi2)−n(∑i=1nyi)2
S
x
y
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
(
y
i
−
y
ˉ
)
=
∑
i
=
1
n
x
i
y
i
−
(
∑
i
=
1
n
x
i
)
(
∑
i
=
1
n
y
i
)
n
S_{xy}=\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)= \sum_{i=1}^{n}x_{i}y_{i}-\frac{{\color{Red}(\sum_{i=1}^{n}x_{i})(\sum_{i=1}^{n}y_{i})}}{n}
Sxy=i=1∑n(xi−xˉ)(yi−yˉ)=i=1∑nxiyi−n(∑i=1nxi)(∑i=1nyi)文章来源地址https://www.toymoban.com/news/detail-520547.html
到了这里,关于样本方差的简化计算公式的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!