机器学习-线性代数-4-解方程组-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器学习-线性代数-4-解方程组。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

解方程组

一、从空间映射的角度研究方程组

对于如下方程组：

$a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b1\\ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b2\\....\\a_{m1}x_1 + a_{m2}x_2 + ... + a_{mn}x_n = bm$

这是一个 $n$ 元方程组，一共包含 $m$ 个方程，将其转换成矩阵乘法形式：

$\left [ \begin{matrix} a_{11}~a_{12}~...~ a_{1n}\\ a_{21}~a_{22}~...~ a_{2n} \\...\\a_{m1}~a_{m2}~...~ a_{mn}\end{matrix} \right ]\left[\begin{matrix} x_1 \\x_2\\...\\x_n\end{matrix} \right] = \left[\begin{matrix} b_1 \\b_2\\...\\b_m\end{matrix} \right]$

令 $\left [ \begin{matrix} a_{11}~a_{12}~...~ a_{1n}\\ a_{21}~a_{22}~...~ a_{2n} \\...\\a_{m1}~a_{m2}~...~ a_{mn}\end{matrix} \right ]$ , $\left[\begin{matrix} x_1 \\x_2\\...\\x_n\end{matrix} \right]$ , $\left[\begin{matrix} b_1 \\b_2\\...\\b_m\end{matrix} \right]$

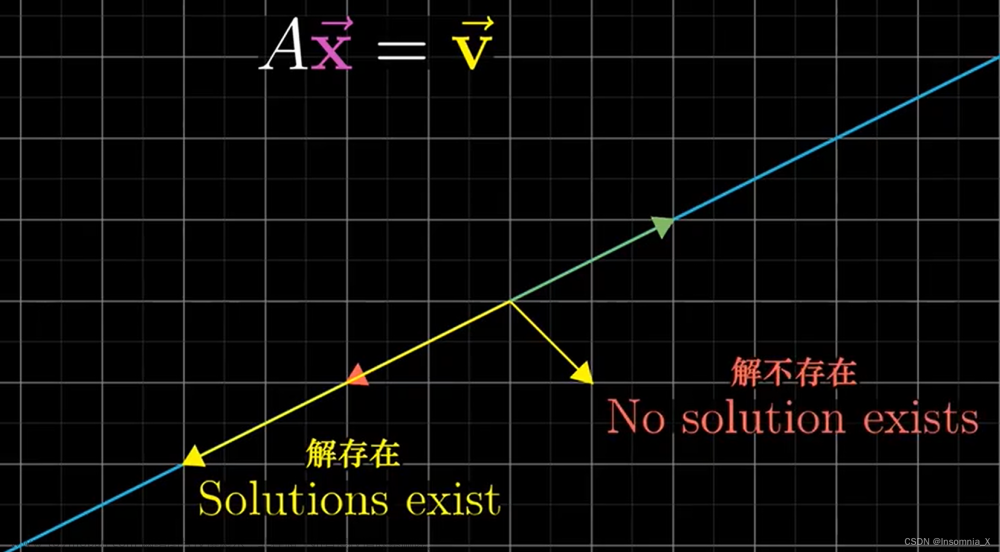
由此转变成了矩阵乘法形式： $A x = b$ ，由此而理解就是：已知目标空间向量 $b$ ，和描述空间映射的矩阵 $A$ ,我们去寻找位于原空间中映射过来的向量 $x$

二、方程解的个数

如果方程有解，即满足 $A x = b$ ，向量 $b$ 就是矩阵 $A$ 的各个列向量的线性组合，换句话说 $b$ 在矩阵 $A$ 的列空间上，才满足方程组有解。

为了后续进一步探索，再次明确几个名词的含义：

秩 $r$ :矩阵列空间的维度，也是映射后向量集合构成子空间的维度。

$m$ ：矩阵的行数，也是目标空间的维度

$n$ :矩阵的列数，就是映射前原空间的维度

明确了这些，我们继续进行讨论：

1. r = m = n

描述的是一个方阵，而且是满秩矩阵。这首先意味着原空间和列空间维数相等，都是 $R^r$ 空间，映射的过程不存在空间的压缩;同时目标空间和列空间等维，也都是 $R^r$ 空间，意味着目标空间 $R^m$ (也就是 $R^r$ )中的任意一个向量都在矩阵A的列空间上，这意味着什么?意味着在这种情况下，方程组一定有解，且仅有一个解。
在等式推导上，由于满秩方阵A可逆，我们对方程组 $A x = b$ 左右两侧同时乘以 $A$ 的逆矩阵 $A^{-1}$ ，就能得到解向量的表达式:
$Ax =b→A^{-1}Ax =A^{-1}b→x =A^{-1}b$

2. r = n < m

$r = n$ 意味着，映射后的列空间和原空间的维数相等，都是 $n$ ，即如果在列空间上任选一个向量 $b$ ，在原空间中与之对应的解向量 $x$ 是唯一的。但是请注意，由于 $r < m$ ，列空间的维度小于目标空间的维度，列空间仅仅是目标空间 $R^m$ 的一个子空间，因此问题来了，如果我们在目标空间中挑选的 $b$ 向量不在列空间上，那么方程就无解。因此在这种情况下，方程组要么无解，要么有唯一解，区分的原则就是 $b$ 向量是否在 $A$ 的列空间上。

3. r = m < n

$r = m$ 意味着目标空间是一个 $R^m$ 空间，而列空间和目标空间维数相等，同样是 $R^m$ 空间，同样说明目标空间里的所有向量都位于矩阵 $A$ 的列空间上，因此方程组一定有解。而同时有 $r < n$ ，意味着列空间的维度小于原空间的维度，即映射存在空间的压缩。因此A是一个多对一的空间压缩矩阵，方程组有解，且解有无数个。

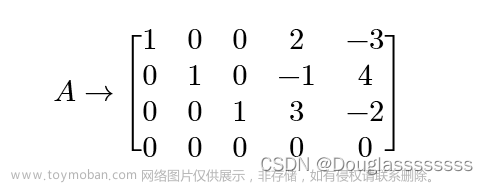
4. r < m 且 r < n

这种情况包含了2、3小点的情况，具体的说 $r$ 是原空间和目标空间的子空间，此时既可能无解也可能无解。

三、方程组解求法

当方程组有唯一解的时候，他的解就是一个向量: $\left[\begin{matrix} x_1 \\x_2\\...\\x_n\end{matrix} \right]$ ，这是唯一的表达方式。
但是如果方程组有无数种解，显然我们无法将其全部罗列出来，具体应该如何表达呢?我们还是从解的集合意义出发:
当方程组有无数个解的时候，实质上就构成了一个解的空间。我们的目标就是要找到这个解空间的描述方式，我们的思路是:
首先任意找一个满足方程组的解，也就是解空间中的一个任意点，我们称其为特殊解: $x_p$ ，此时满足 $Ax_p=b$ 。
然后我们转而去考虑零空间。根据定义，零空间中的任意点 $x_。$ 满足 $Ax_。 =0$ ，那么此时就有 $Ax_p + Ax_。 = b+0= A(x_p+x_。)= b$ 。这意味着什么?意味着解空间中任意一个解向量与零空间中任意一个向量相加的结果也是解向量，用向量相加的几何意义来描述就是:零空间里的某个向量沿着这个特解向量x,进行移动，移动后的结果是另外一个解向量。那么整个零空间沿着这个特殊解向量 $x_p$ 进行移动，其结果就是我们要找的解空间了。