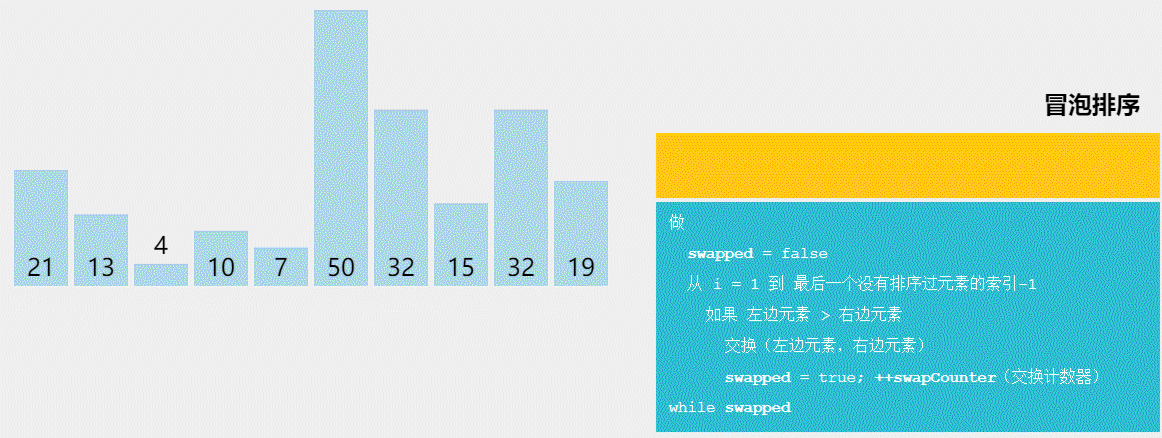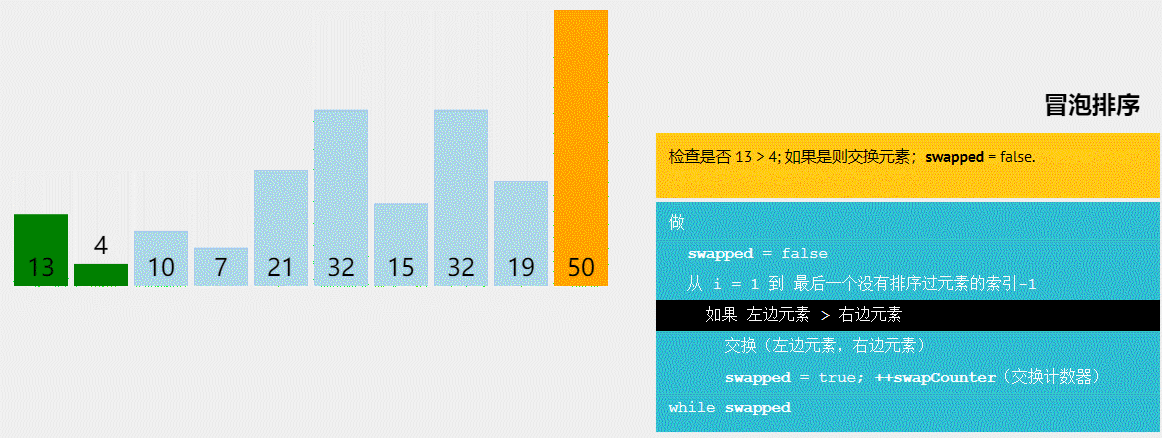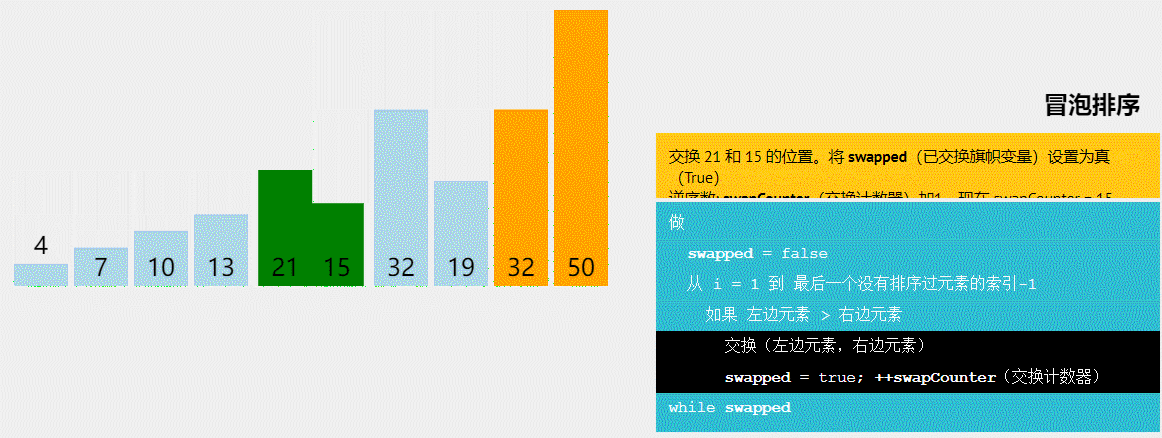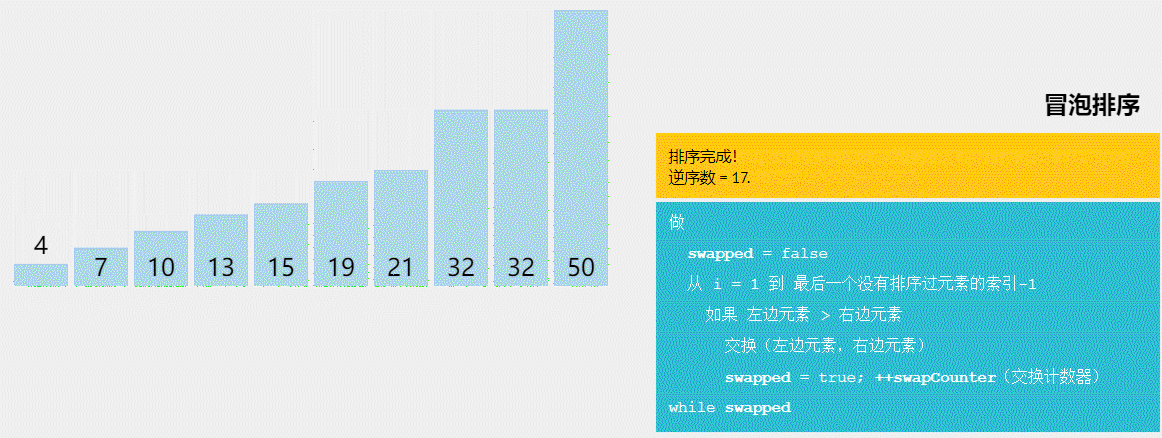https://blog.csdn.net/weixin_30342639/article/details/105343780
#include
#include
#include
#include
using namespace std;
// https://blog.csdn.net/weixin_30342639/article/details/105343780
总览
1、选择排序- 不稳定!
2、冒泡排序-稳定
3、插入排序-稳定
4、快排
5、堆排
6、归并排序–稳定
(稳定的只有插入、冒泡、归并)
下面是非比较排序,稳定与否就不要记了。(好像都是稳定的)
7、希尔排序(插入排序的一种)–不稳定!
是插入排序的改进版本,基于分组的思想
8、计数排序 时间复杂度是O(n),很低,代价是空间复杂度很大,为O(n),不稳定
计数排序会创建一个临时的数组,里面存放每个数出现的次数。
计数排序仅适合数据跨度不大的场景。
9、桶排序 复杂度:桶排序执行的高效与否和是否是稳定的取决于哈希散列的算法以及内部排序的结果
桶排序类似于哈希表,通过一定的映射规则将数组中的元素映射到不同的桶中,每个桶内进行内部排序,最后将每个桶按顺序输出就行了。
桶排序执行的高效与否和是否是稳定的取决于哈希散列的算法以及内部排序的结果。
需要注意的是,这个映射算法并不是常规的映射算法,要求是每个桶中的所有数都要比前一个桶中的所有数都要大,这样最后输出的才是一个排好序的结果。
比如说第一个桶中存1-30的数字,第二个桶中存31-60的数字,第三个桶中存61-90的数字...
10、基数排序 复杂度就不要记了
不是很了解
1 选择排序----了解即可
//时间复杂度O(N2),空间复杂度O(1)
//算法:第一次遍历找到最小的,和第一个元素交换。第二次遍历找到最小的,和第二个元素交换
class Solution1
{
public:
void sort(vector<int>& nums)
{
int n=nums.size();
for(int i=0;i<n;i++)
{
int minindex=i;
for(int j=i;j<n;j++)
{
if(nums[j]<nums[i])
minindex=j;
}
swap(nums[i],nums[minindex]);
}
return ;
}
};
2–冒泡排序—了解即可–时间复杂度太高
//时间复杂度O(N2) 空间复杂度O(1)
//算法流程:从前往后遍历,两两比较。将大的放在后面。遍历完一次后,数组的最后一个元素就是最大的。遍历n次
class Solution2
{
public:
void sort(vector<int> & nums)
{
int n=nums.size();
for(int i=0;i<n-1;i++)
{
for(int j=0;j<n-i-1;j++)
{
if(nums[j]>nums[j+1])
swap(nums[j],nums[j+1]);
}
}
return ;
}
};
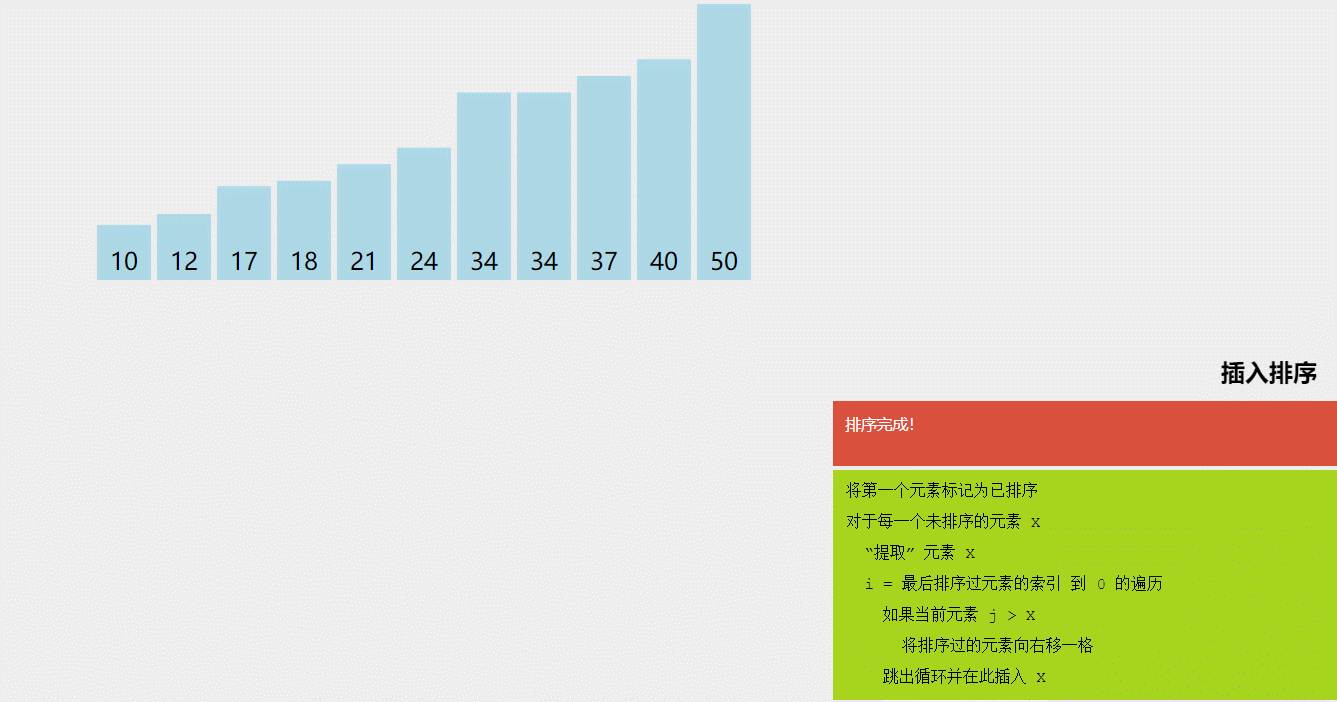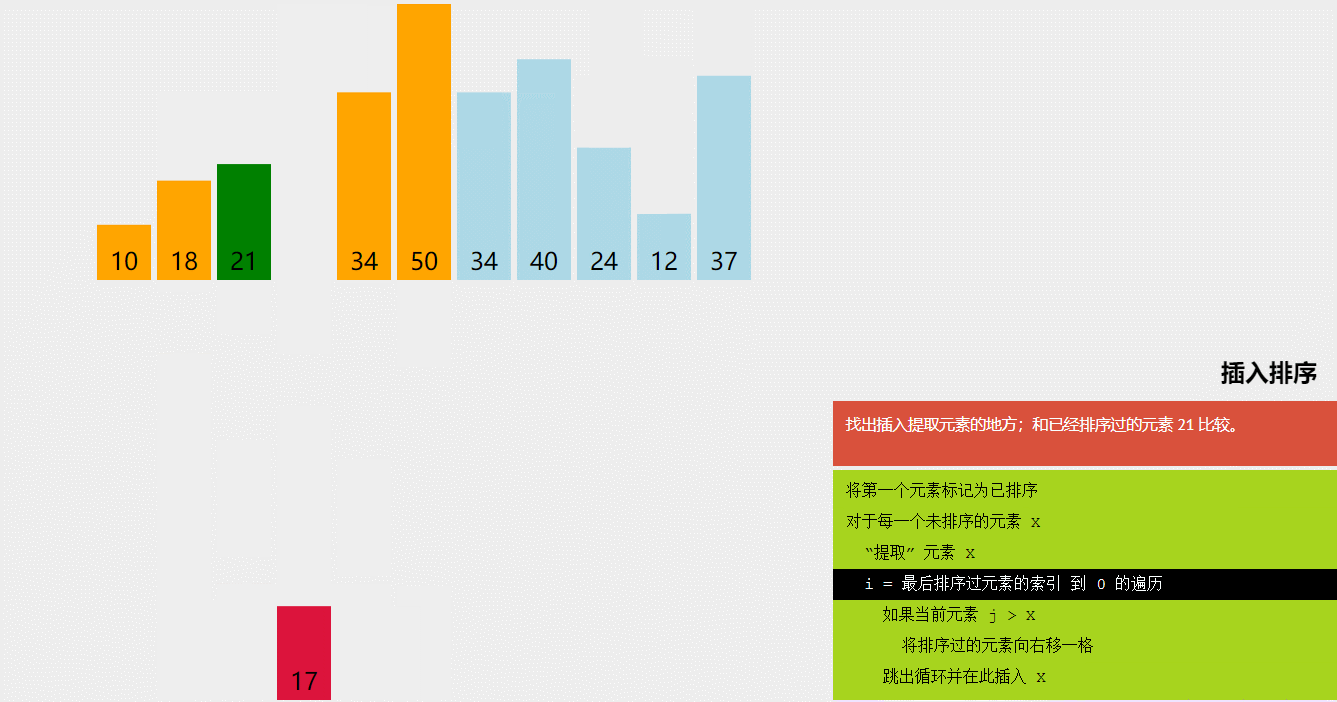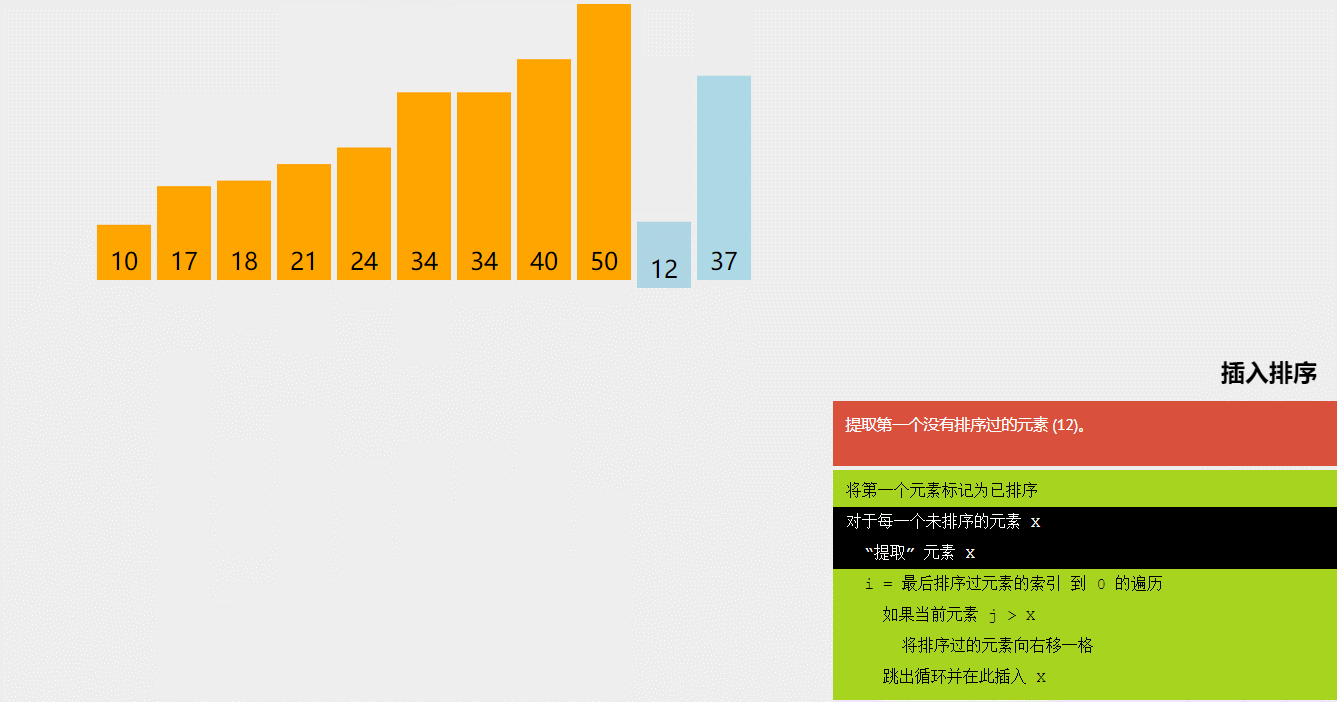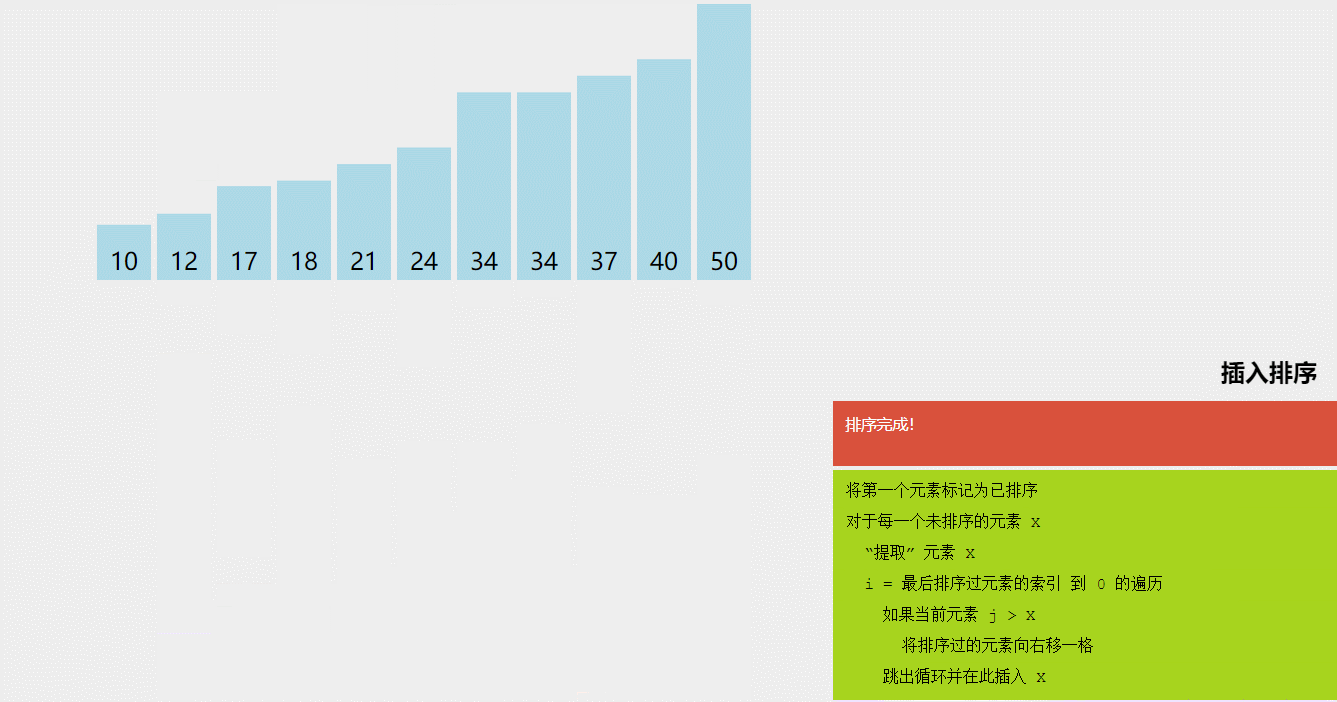
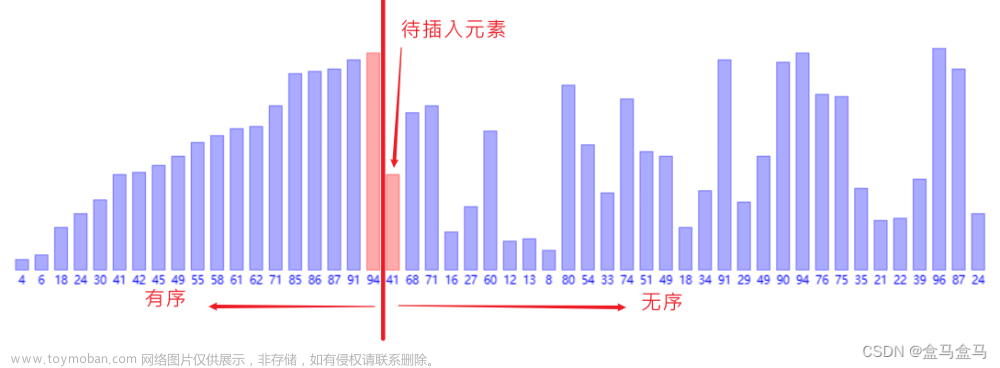
3-插入排序–重点
//时间复杂度O(n2),,空间复杂度O(1),并且是稳定的
//之所以必上面两种时间复杂度好,是因为,他在数组的有序的部分,不会进行多余的比较。也就是,在基本有序时,时间复杂度会接近O(N)
class Solution3
{
public:
void sort(vector<int> & nums)
{
int n=nums.size();
for(int i=1;i<n;i++)
{
for(int j=i;j>0;j--)
{
if(nums[j]<nums[j-1])
swap(nums[j],nums[j-1]);
else
break;
}
}
return ;
}
};
上面三种是基本的排序,后面是高阶的时间复杂度格更低的排序
4–快速排序
//1 版本1–
//每次确定一个元素的位置
class Solution3
{
public:
void quicksort(vector<int> & nums)
{
int n=nums.size();
process(nums,0,n-1);
return ;
}
//这个函数将L~R的位置的元素排好序
void process(vector<int>& nums,int L,int R )
{
if(L>=R) return ;
int mid=partition(nums,L,R);
process(nums,L,mid-1);
process(nums,mid+1,R);
}
//这个函数以nums最右边的元素作为基准,将其放在其应该在的位置,小于等于nusm[r]的防左边
int partition(vector<int> & nums,int L,int R)
{
if(L>R)
{
return -1;
}
if(L==R)
{
return L;
}
int prewrite=L;
int index=L;
while(index<R)
{
if(nums[index]<=nums[R])
{
swap(nums[index],nums[prewrite]);
prewrite++;
}
index++;
}
swap(nums[prewrite],nums[R]);
return prewrite;
}
};
版本2–每次确定一组值相同的元素的位置:
class Solution3
{
public:
void quicksort(vector<int> & nums)
{
int n=nums.size();
process(nums,0,n-1);
}
//这个函数将L~R的位置的元素排好序
void process(vector<int>& nums,int L,int R )
{
//递归的base-case
if(L>=R)
{
return ;
}
vector<int> equalarea =partition(nums,L,R);
process(nums,L,equalarea[0]-1);
process(nums,equalarea[1]+1,R);
}
//这个函数以nums最右边的元素作为基准,将其放在其应该在的位置,小于等于nusm[r]的防左边
//注意的是less指针和more指针的含义不再是待改写的指针,而是已经完成排序的边界,也就是完成的排序的范围是[,less]和[more,]。也就是说,待改写的区域是(less,more),而不是[less,more]
vector<int> partition(vector<int> & nums,int L,int R)
{
if(L>R)
return{-1,-1};
if(L==R)
{
return{L,R};
}
int less=L-1;
int more=R;
int index=L;
while(index<more)
{
if(nums[index]==nums[R])
{
index++;
}
else if(nums[index]<nums[R])
{
swap(nums[++less],nums[index]);
index++;
}
else if(nums[index]>nums[R])
{
swap(nums[index],nums[--more]);
//index并不变化
}
}
swap(nums[more],nums[R]);
return {less+1,more};
}
};
版本三:最终版本
class Solution
{
public:
vector<int> quicksort(vector<int>& nums)
{
int n=nums.size();
process(nums,0,n-1);
return nums;
}
void process(vector<int>& nums,int L,int R)
{
if(L>=R)
{
return;
}
int temp=rand()%(R-L+1);
swap(nums[L+temp],nums[R]);
vector<int> equalarea=partition(nums,L,R);
process(nums,L,equalarea[0]-1);
process(nums,equalarea[1]+1,R);
}
vector<int> partition(vector<int>& nums,int L,int R)
{
if(L>R)
return{-1,-1};
if(L==R)
return {L,L};
int less=L-1;
int more=R;
int index=L;
while(index<more)
{
if(nums[index]==nums[R])
index++;
else if(nums[index]<nums[R])
{
swap(nums[index],nums[++less]);
index++;
}
else if(nums[index]>nums[R])
{
swap(nums[index],nums[--more]);
}
}
swap(nums[more],nums[R]);
return {less+1,more};
}
};
int main()
{
vector<int> nums{1,4,3,6,5,8,9,4};
Solution1 slu;
slu.sort(nums);
for(auto it:nums)
{
cout<<it<<endl;
}
return 0;
}
5 归并排序
class Solution
{
public:
vector<int> sortArray(vector<int> & nums)
{
int l=0;
int r=nums.size()-1;
mergesort(nums,l,r);
return nums;
}
//将left到right变为有序的
void mergesort(vector<int>&nums,int left,int right)
{
//base_case
if(left==right)
return;
int mid=left+(right-left)/2;
//将left到mid变为有序的
mergesort(nums,left,mid);
//将mid到right变为有序的
mergesort(nums,mid+1,right);
//merge的过程,mid两侧有序的数组合并为整个数组有序的
merge(nums,left,mid,right);
}
void merge(vector<int> & nums,int L,int M,int R)
{
vector<int> temp(R-L+1);
int i=0;
//左侧数据的起始的位置
int p1=L;
//右侧数据的起始的位置
int p2=M+1;
while(p1<=M && p2<=R)
{
if(nums[p1]<nums[p2])
{
temp[i]=nums[p1];
p1++;
}
else
{
temp[i]=nums[p2];
p2++;
}
i++;
}
while(p1<=M)
{
temp[i]=nums[p1];
p1++;
i++;
}
while(p2<=R)
{
temp[i]=nums[p2];
p2++;
i++;
}
for(int i=0;i<temp.size();i++)
{
nums[L+i]=temp[i];
}
}
};
堆排—小根堆排序
i 结点的父结点 par = floor((i-1)/2) 「向下取整」
i 结点的左子结点 2 * i +1
i 结点的右子结点 2 * i + 2
//模拟priority_queue文章来源:https://www.toymoban.com/news/detail-521645.html
class Heap
{
public:
vector<int> vec;
int capacity;
int count;
void swapNode(int i,int j)
{
swap(vec[i],vec[j]);
}
//小根堆的上浮操作---在堆中将index节点上浮
void siftup_minheap(int index)
{
if(index==0) return;
cout<<"..."<<endl;
int parentNode=(index-1)/2;
while(parentNode>=0)
{
if(vec[parentNode]<vec[index])
break;//父节点比这个节点小,则停止上滤
swapNode(index,parentNode);
index=parentNode;
if(index==0) break;
parentNode=(index-1)/2;
}
}
//小根堆的下沉操作--下沉的范围是[index,n),一般是vec.size()
void siftdown_minheap(int index,int n)
{
int i=index;
int j=2*i+1;//index节点的左儿子
while(j<n)
{
if(j+1<n && vec[j+1]<vec[j]) j++;//j是左儿子和右儿子。较小的那个的下标
if(vec[i]<vec[j]) break;//如果 当前节点比两个孩子都要小,那么停止下沉
swapNode(i,j);
i=j;
j=2*i+1;
}
}
//小根堆的插入操作
void insert(int num)
{
vec.push_back(num);
int index=vec.size();
siftup_minheap(index-1);
}
//小根堆的删除堆顶元素操作--先将根节点和末尾元素互换,然后popback,然后从根节点开始下沉
void del()
{
int n=vec.size();
swapNode(0,n-1);
vec.pop_back();
siftdown_minheap(0,vec.size());
}
//原地建堆的操作--复杂度是NlogN
void buildHeap_1()
{
for(int i=0;i<vec.size();i++)
{
siftup_minheap(i);
}
}
//时间复杂度是N的,建堆方法--从第一个非叶子节点,往前遍历,并进行下沉操作
//根节点是0开始编号的时候,第一个非叶子节点是最后一个节点的父节点,也就是(n-1-1)/2=(n-2)/2
void buildHeap()
{
int n=vec.size();
for(int i=(n-2)/2;i>=0;i--)
{
siftdown_minheap(i,vec.size());
}
}
int top()
{
int temp=vec[0];
return temp;
}
public:
Heap(vector<int>& vec_)
{
vec=vec_;
}
};
int main()
{
vector<int> vec{9,4,7,1,5,3};
Heap heap_(vec);
heap_.buildHeap();
while(heap_.vec.size()>0)
{
cout<<heap_.top()<<endl;
heap_.del();
}
return 0;
}
//稳定性:只有冒泡、插入、归并,这三个是稳定性的排序算法。文章来源地址https://www.toymoban.com/news/detail-521645.html
到了这里,关于排序算法汇总的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!