前言:本人的课题是关于EIT采集系统设计,所谓的EIT,简单的说就是往人体注入特定频率的电流信号,通过采集反馈的电压信号,进而使用成像算法重构人体内部的阻抗分布。由于采集到的电压包含其它频率的热噪声,为了只保留注入频率的信号成分,需要对采集到的电压信号进行FFT处理。
在本文应用中,FFT相当于一个带通滤波器,用于获取指定频率的信号信息。关于快速傅里叶变化这里不做过多的介绍,具体可参考别人写的博客:
如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程)_Xav Zewen的博客
本文主要介绍如何在STM32F407上实现对特定频率进行FFT。重新更新并完善了一下,将代码整理为函数,方便读者调用。
一、使用DSP库进行FFT计算
1.1 DSP库开启
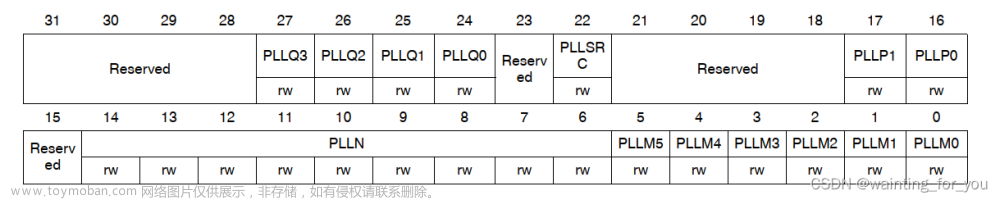
我们知道,相比于整形运算,浮点运算会大量消耗算力,若直接让STM32强行计算,难以满足实时性的需求。好在STM32F407是具有浮点运算(FPU)功能,可以通过MDK配置:target->Roating Point Hardware->Use Single Precison中打开。

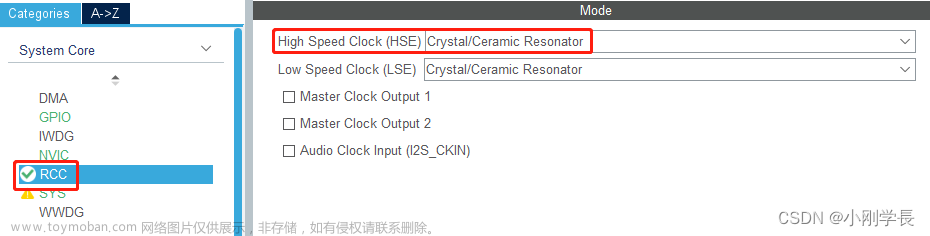
在进行FFT计算时,我们还需要用到三角计算,因此我们还需要添加dsp数学库,调用库中的函数进行数学运算。DSP库的开启如下所示。

同时在MDK配置中添加头文件:ARM_MATH_CM4

通过上述操作,我们便可进入编程环节。
1.2 调用DSP库进行FFT计算
那么,如何通过FFT变换,获取指定频率的幅值信息呢?下面举个例子:
目的:获取电压数据中10kHz的幅值分量
要求:待计算的频率、ADC的采样频率、采集样本量、数据点N 应该满足以下等式:
在STM32程序中,我们可以通过中断设定ADC的采样频率,进而配平上述等式。如定义一个1us定时器中断,在中断任务中执行一次ADC采集(此时采样频率为1MHz),一共采集1000次。
此时FFT的参数为:
待计算的频率——10kHz
ADC的采样频率——1MHz
采集样本量——1000
配平上述式子,求得数据点 N = 10。
【注】 1. 若等式配不平,会导致频谱泄露,造成数据失真;
2. 采样依旧要满足采样定理,即:ADC的采样频率 >2*电压数据中最大的频率分量;
3. 由于FFT变换的特点,采集样本量为2的指数倍能提高计算速度。
使用DSP库进行FFT变换的函数如下:
// FFT计算函数
// *DATA: 导入待FFT计算的原始数组指针
// num:采集样本量
// N:需要保存的第几个数据点
float FFT_Calculation(float *DATA, int num, int N)
{
float array_FFT_output[num]; //储存FFT变换后的512个数据
float array_arm_cmplx_mag[num]; //储存FFT变换后的512个数据的幅值信息
arm_rfft_fast_instance_f32 S;
arm_rfft_fast_init_f32(&S, fftSize); //初始化结构体S中的参数
arm_rfft_fast_f32(&S, array_f32, array_FFT_output, 0); //fft正变换
arm_cmplx_mag_f32(array_FFT_output, array_arm_cmplx_mag, num); //计算幅值
return array_arm_cmplx_mag[N];
} 下面简单的示范一下这个函数怎么使用:
float Data_FFT[1000]; // 待FFT计算的原始数据(读者自行赋值)
float result;
result = FFT_Calculation(Data_FFT,1000,10); // 1000个采样点数,需要保存第10个频点二、FFT算法的优化:使用DFT计算单一频点信息
虽然FFT计算十分方便,但是,当我们只需要单一频点数据时,FFT由于计算了大量的无效数据,消耗了算力。在上面的例子中,我们只需要获得10kHz的电压幅值,这时代码可以优化为离散型傅里叶变化(DFT)。离散型傅里叶变化的计算公式如下:

离散型傅里叶变换(DFT)的计算代码如下:
#include "arm_math.h" // 代码中涉及了sin cos 计算, 需按1.1小节开启DSP库
// *Data: 导入待DFT计算的原始数组指针
// num:采集样本量
// N:需要保存的第几个数据点
float DFT_Calculation(float *Data, int num, int N)
{
unsigned int i;
float SUM_Re = 0; //实频数值
float SUM_Im = 0; //虚频数值
float result = 0; // 计算结果
//FFT展开式
for(i=0;i<num;i++)
{
SUM_Re = SUM_Re + Data[i]*cos(2*3.1415926*N*i/num);
SUM_Im = SUM_Im - Data[i]*sin(2*3.1415926*N*i/num);
}
//计算幅值
result = sqrt(SUM_Re*SUM_Re + SUM_Im*SUM_Im);
return result;
}该函数的使用方法同FFT一致:
float Data_DFT[1000]; // 待DFT计算的原始数据(读者自行赋值)
float result;
result = DFT_Calculation(Data_DFT,1000,10); // 1000个采样点数,需要保存第10个频点经过测试,计算单一频点信息时,使用DFT算法相比于FFT,时间节省了约51%。
进一步提升
如果代码对于实时性有要求,在内存和算力的寸土寸金的单片机上,可以通过查表法,代替耗时的三角函数计算。文章来源:https://www.toymoban.com/news/detail-521672.html
如上面的代码, cos(2*3.1415926*N*i/num) 和 sin(2*3.1415926*N*i/num) 的计算结果是固定值,可以提前计算出N=1000,k=10,i取0~999时的cos和sin值,在DFT计算是查询预先计算好的三角函数值,以节省算力。文章来源地址https://www.toymoban.com/news/detail-521672.html
到了这里,关于基于STM32F407实现快速傅里叶变化(FFT),计算指定频率的幅值的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!