[python][pcl]python-pcl案例之基于多项式重构的平滑和正态估计重采样-Toy模板网

这篇具有很好参考价值的文章主要介绍了[python][pcl]python-pcl案例之基于多项式重构的平滑和正态估计重采样。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

测试环境：

pcl==1.12.1

python-pcl==0.3.1

python==3.7

代码：

# -*- coding: utf-8 -*-
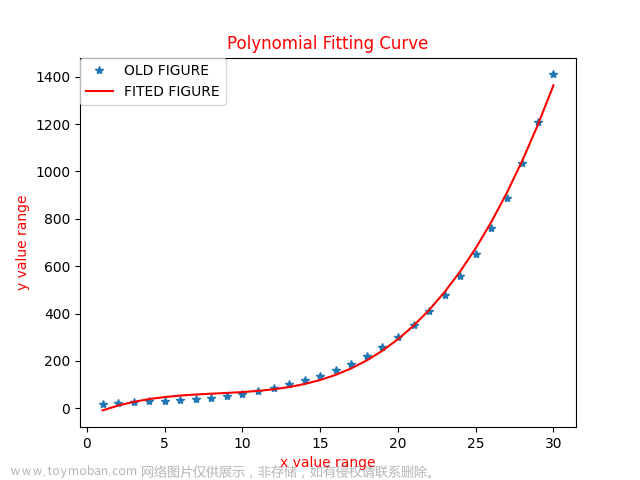
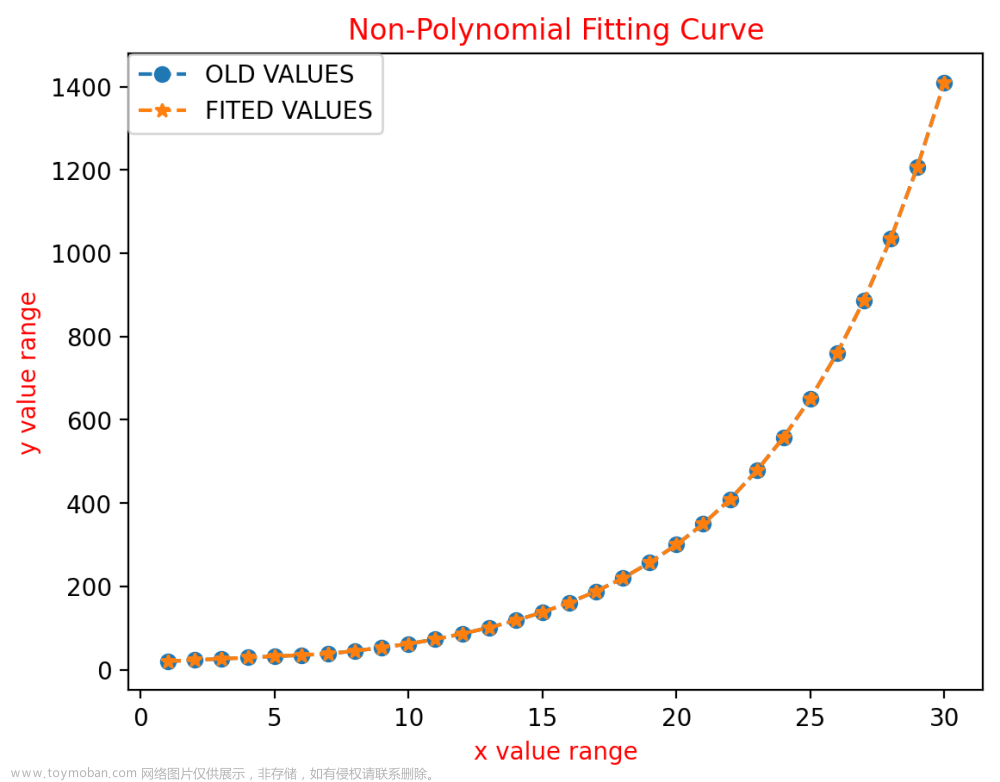
# Smoothing and normal estimation based on polynomial reconstruction
# http://pointclouds.org/documentation/tutorials/resampling.php#moving-least-squares

import numpy as np
import pcl
import random


def main():
    # // Load input file into a PointCloud<T> with an appropriate type
    # pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ> ());
    # // Load bun0.pcd -- should be available with the PCL archive in test
    # pcl::io::loadPCDFile ("bun0.pcd", *cloud);
    cloud = pcl.load('bun0.pcd')
    print('cloud(size) = ' + str(cloud.size))

    # // Create a KD-Tree
    # pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ>);
    tree = cloud.make_kdtree()
    # tree = cloud.make_kdtree_flann()
    # blankCloud = pcl.PointCloud()
    # tree = blankCloud.make_kdtree()

    # // Output has the PointNormal type in order to store the normals calculated by MLS
    # pcl::PointCloud<pcl::PointNormal> mls_points;
    # mls_points = pcl.PointCloudNormal()
    # // Init object (second point type is for the normals, even if unused)
    # pcl::MovingLeastSquares<pcl::PointXYZ, pcl::PointNormal> mls;
    # mls.setComputeNormals (true);
    #
    # // Set parameters
    # mls.setInputCloud (cloud);
    # mls.setPolynomialFit (true);
    # mls.setSearchMethod (tree);
    # mls.setSearchRadius (0.03);
    #
    # // Reconstruct
    # mls.process (mls_points);
    mls = cloud.make_moving_least_squares()
    # print('make_moving_least_squares')
    mls.set_Compute_Normals(True)
    mls.set_polynomial_fit(True)
    mls.set_Search_Method(tree)
    mls.set_search_radius(0.03)
    print('set parameters')
    mls_points = mls.process()

    # Save output
    # pcl::io::savePCDFile ("bun0-mls.pcd", mls_points);
    pcl.save_PointNormal(mls_points, 'bun0-mls.pcd')


if __name__ == "__main__":
    # import cProfile
    # cProfile.run('main()', sort='time')
    main()

运行结果：

cloud(size) = 112586
set parameters

bun0.pcd文件需要去这个地址下载：https://github.com/strawlab/python-pcl/blob/master/examples/official/Surface/bun0.pcd文章来源地址https://www.toymoban.com/news/detail-521999.html

到了这里，关于[python][pcl]python-pcl案例之基于多项式重构的平滑和正态估计重采样的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！