【数值分析实验】（一）插值法（含matlab代码）

1 背景简介

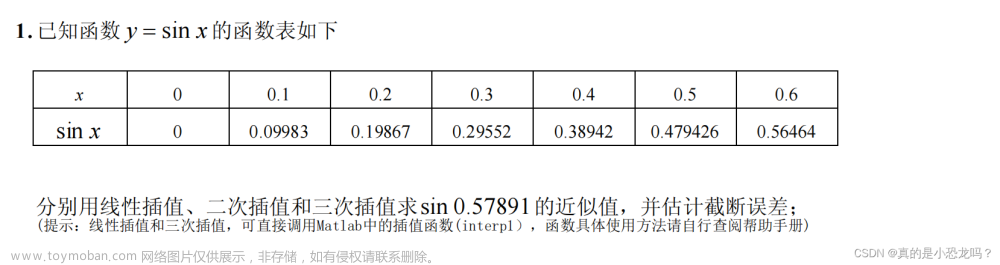
        实际问题中许多变量的关系可以用数学函数概念进行刻画，但是在大多数情况下，这些函数的表达式是未知的，或者已知但十分复杂，需要我们将这个函数的未知解析式近似地构造出来，或者用一个简单的函数表达式来代替复杂的函数表达式。基于上述过程，我们设计实验，通过提供未知函数或复杂函数的某些已知信息，来实现以下目的：
        (1)构造该函数的近似表达式；
        (2)计算该函数在其他点处的函数值；
        (3)计算所构造的近似表达式与真实函数的误差。

2 案例设计

3 数学模型

3.1 拉格朗日插值法

3.1.1 算法过程

3.1.2 代码

function y=Lagrange(xi,fx,x)
xi_num=length(xi); % 已知节点的个数
x_num=length(x);   % 需要估计的节点个数
for i=1:x_num      % 对每个估计节点执行循环
    z=x(i);
    f=0.0;
    for m=1:xi_num
        L=1.0;     % L为基函数
        for n=1:xi_num
            if n~=m
                L=L*(z-xi(n))/(xi(m)-xi(n));
            end
        end
        f=L*fx(m)+f; 
    end
    y(i)=f;
end
end

%% 输入参数
% 输入节点
xi=(1:2:11); 
% 输入节点处函数值
fx=[2.7183 2.2317 5.9365 22.3803 100.0381 494.8276];
% 输入需要估计的节点
x=[3.57 6.91 9.36];
%% 利用Lagrange计算x处函数值
y=Lagrange(xi,fx,x) % 结果为y=[1.5326 21.1960 135.2998]

3.1.3 计算结果

3.2 牛顿插值法

3.2.1 算法过程

3.2.2 代码

function y=Newton(x,xi,yi)
xi_num=length(xi); % 已知节点的个数
x_num=length(x);   % 需要估计的节点个数
f=zeros(xi_num,xi_num);
for i=1:x_num      % 对每个估计节点执行循环
    z=x(i);
    N=0.0;
    for m=1:xi_num
        f(m)=yi(m);
    end
    for n=2:xi_num % 构造差商表   
        for m=n:xi_num
            f(m,n)=(f(m,n-1)-f(m-1,n-1))/(xi(m)-xi(m+1-n));
        end
    end
    for m=2:xi_num
        t=1;
        for j=1:m-1
            t=t*(z-xi(j));
        end
        N=f(m,m)*t+N;
    end
    N=f(1,1)+N;
    y(i)=N;
end
disp('差商表如下：');
disp(f);
end

%% 输入参数
% 输入节点
xi=(1:2:11); 
% 输入节点处函数值
fx=[2.7183 2.2317 5.9365 22.3803 100.0381 494.8276];
% 输入需要估计的节点
x=[3.57 6.91 9.36];
%% 利用Newton计算x处函数值
y=Newton(x,xi,fx) % 结果为y=[2.7854 20.9903 132.5689]

3.2.3 计算结果

3.3 埃尔米特插值法

3.3.1 算法过程

3.3.2 代码

function y=Hermite(xi,fx,fx1,x)
xi_num=length(xi); % 已知节点的个数
x_num=length(x);   % 需要估计的节点个数
for i=1:x_num
    f=0.0;
    for m=1:xi_num
        H=1.0;
        a=0.0;
        for n=1:xi_num
            if n~=m
                H=H*((x(i)-xi(n))/(xi(m)-xi(n)))^2;
                a=a+1/(xi(m)-xi(n));
            end
        end
        f=f+H*((xi(m)-x(i))*(2*a*fx(m)-fx1(m))+fx(m));
    end
    y(i)=f;
end

%% 输入参数
% 输入节点
xi=(1:2:11); 
% 输入节点处函数值
fx=[2.7183 2.2317 5.9365 22.3803 100.0381 494.8276];
% 输入节点处导数值
fx1=[-2.7183 0.7439 3.5619 15.9859 77.8074 404.8590];
% 输入需要估计的节点
x=[3.57 6.91 9.36];
%% 利用Lagrange计算x处函数值
y=Hermite(xi,fx,fx1,x) % 结果为y=[2.7854 20.9903 132.5689]

3.3.3 计算结果

4 分析与讨论

        在本设计案例中，三种插值方法都能够有效地估算插值节点外其他点的函数值，插值结果也比较接近真实值。其中，埃尔米特插值法需要用到被插函数的导数信息，估计误差最小，效果最好。而拉格朗日插值方法和牛顿插值法的估计精度相同且次于埃尔米特插值法。
文章来源地址https://www.toymoban.com/news/detail-522220.html

到了这里，关于【数值分析实验】（一）插值法（含matlab代码）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！