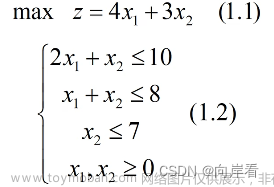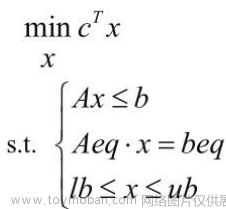奶制品的生产与销售
一 问题重述
1.1问题背景
工厂根据外部需求和内部设备,人力,原料等条件,以及最大利润为生产目标制定生产计划,根据生产计划,工艺流程,资源约束及费用参数等,以最小的成本为目标制定生产批量计划,若短时间外部需求和内部资源等不随时间的变化,可制定单阶段生产计划,否则应制定多阶段的生产计划。
1.2问题提出
1.21问题一
问题引言:加工奶制品的生产计划,一桶牛奶生产A1需要12h获利24元/kg,生产A2需要8h获利16元/kg,每天50桶牛奶,480h的时间,且最多只能加工100kg的A1。怎末制定生产计划,才能使得每天获利最大。
(1)为了使每天的获利最大,35元可以购买一同牛奶在进行加工,需要购买吗?如果购买,那么每天最多买多少呢?
(2)可聘用临时工人,那么最多可以付出工资是每小时几元?
(3)如果A1的获利在增加到30元/kg,是否要改变生产计划?
1.22问题二
问题引言:在问题一的基础上,在A的基础上深加工可获得B产品,每千克A1经过两小时可以加工成0.8kg的B1,同时支付3元加工费,每千克可以从中获利44元。每千克A2经过两小时可以加工成0.75kg的B2,同时支付3元加工费,每千克可以从中获利32元.
(1)30元可增加1桶牛奶,3元可增加1h时间,应否投资?现投资150元,可赚回多少?
(2)B1,B2的获利经常有10%的波动,对计划有无影响?
(3)每天销售10kg的A1的合同必须满足,对利润有什么影响?
二 问题分析
由于产品利润、加工时间等均为常数,可建立线性规划模型。通过决策变量,目标函数,约束条件这三个线性规划模型要素进行规划,用LINGO求解,输出丰富,利用影子价格和灵敏性分析可对结果做进一步研究。
三、模型假设符号说明
3.1 模型假设
1.假设生产中没有原料的浪费。
2.A1 ,A2每千克的获利是与各自产量无关的常数。
3.每桶牛奶加工A1 ,A2的数量, 时间是与各自产量无关的常数。
4.A1 ,A2每千克的获利是与相互产量无关的常数。
5.每桶牛奶加工A1 ,A2的数量,时间是与相互产量无关的常数。
6.加工A1 ,A2的牛奶桶数是实数
7.假设工人生产的速率相等。
8.假设不考虑市场波动带来收益不同的问题。
9.假设生产的机器没有故障。
10.假设从A深加工到B时没有原料损失。
3.2 符号说明

表 1 符号说明
四、模型建立及求解
4.1 问题 1 的建模求解
问题(1)
1.模型准备
设x1桶牛奶生产A1,则可获利为72x1,设x2桶牛奶生产A2,则可获利为64x2,则每天获利为:max Z=72x1+64x2,通过所知的信息确定以下的约束条件: ##### 2.基于线性规划模型的建立
##### 2.基于线性规划模型的建立
由模型准备中的约束条件,运用图解法画出约束范围如下:
目标函数和约束条件是线性函数,可行域为直线段围成的凸多边形,目标函数的等值线为直线,所以最优解一定在凸多边形的某个顶点取得,由图像分析可知在B(20,30)点得到最优解。
3.模型求解
使用Lingo软件求解线性规划问题可得如下结果:

所以三种资源中原料无剩余,时间无剩余,加工能力剩余40时,其中约束“资源”剩余为零,为有效约束,且20桶牛奶生产A1 , 30桶生产A2,利润最大3360元。
由运行结果可知,原料增加1单位,利润正增长48,时间增加1单位,利润增长2,CPCT为零表示加工能力增长不影响利润。
由于35<48,所以35元可以买到1桶牛奶时,应该买。聘用临时工个人付出的工资最多每小时2元。
Lingo敏感性分析,最优解不变时目标函数系数允许变化范围,约束条件不变,x1系数范围(64,96),x2系数范围(48,72),x1系数由243=72 增加为303=90,在允许范围内。A1获利增加到 30元/kg,不改变生产计划。
结果解释:
影子价格有意义时约束右端的允许变化范围,目标函数不变,原料最多增加10,时间最多增加53,充分条件。
所以35元可买到1桶牛奶, 每天最多买10桶。
问题(2)
1.模型准备
50桶牛奶, 480h,至多100kgA1,制订生产计划,使每天净利润最大。
设x1桶牛奶生产A1,设x2桶牛奶生产A2,x3桶牛奶生产B1,设x4桶牛奶生产B2,x5kg的A1加工B1,x6kg的A2加工B2,则每天获利为:,通过所知的信息确定以下的约束条件:
2.基于线性规划模型的建立
由模型准备中的约束条件,运用Lingo求解如下:
每天销售168 kgA2和19.2 kgB1,利润3460.8(元)8桶牛奶加工成A1,42桶牛奶加工成A2,将得到的24kgA1全部加工成B1。除加工能力外均为紧约束。
3.模型求解

所以增加1桶牛奶使利润增长37.92,增加1h时间使利润增长3.26,投资150元增加5桶牛奶,可赚回189.6元(大于增加时间的利润增长)。
敏感性分析:B1获利下降10%,超出X3 系数允许范围,B2获利上升10%,超
出X4 系数允许范围,波动对计划有影响,B1 ,B2的获利有10%的波动,对计划有无影响。生产计划应重新制订,如将x3的系数改为39.6计算,会发现结果有很大变化。
结果解释:x1从0开始增加一个单位时,最优目标函数值将减少1.68,公司利润减少1.68×10=16.8(元),最优利润为3460.8 – 16.8 = 3444。
五、模型的评价
5.1 模型的优点
1、通过数学关系推导,模型精确度较高;
2、模型的建立根据动态规划模型、几何模型等理论,采用了数学和概率学
原理,所得出的数据和精确度较为严谨精确。
3、模型假设考虑了多种情况,尽可能排除了外界的影响,引入的误差较少
4、本文从研究模型机理开始到模型建立、模型求解、模型验证、模型灵敏
度分析,整体框架较为完整。文章来源:https://www.toymoban.com/news/detail-524368.html
5.2 模型的缺点
分析方法比较具有针对性,推广到实际生活中存在一些误差。Reduced Cost是有意义,有条件的(LINGO没有给出)。文章来源地址https://www.toymoban.com/news/detail-524368.html
到了这里,关于数学建模--Lingo求解线性规划问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!