Prim算法求最小生成树-Toy模板网

这篇具有很好参考价值的文章主要介绍了Prim算法求最小生成树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一.最小生成树

给定一张边带无权的无向图G = （V， E）， n = |V|， m = |E|。由V中全部n个顶点和E中n - 1条边构成的无向连通子图被称为G的一课生成树。边的权值之和最小的生成树被称为无向图的最小生成树。

二.算法描述

Prime算法

Prim算法总是维护最小生成树的一部分。最初，Prim算法仅确定1号节点属于最小生成树。
1.在任意时刻，设已经确定属于最小生成树的节点集合为T，剩余节点集合为S。Prim算法找到两点端点分别属于集合S，T的权值最小的边，然后把点x从集合S中删除，加入到集合T，并把权值累加到答案中。
2.具体来说，可以维护数组d：若x属于S，则d[x]表示节点x与集合T中的节点之间权值最小的边的权值。若x属于T，则d[x]就等于x被加入T时选出的最小的边的权值。
可以类比Dijkstra算法，用一个数组标记节点是否属于T。每次从未被标记的节点中选出d值最小的，把它标记（新加入T），同时扫描所有出边，更新另一个端点的d值。最后，最小生成树的权值总和就是d[x]（∑ x = 2~n）。
3.Prim算法的时间复杂度为O（n^2），可以用二叉堆优化到（mlogn），但用二叉堆优化不如直接使用Kruskal算法更加方便。因此，Prim主要用于稠密图，尤其是完全图的最小生成树的求解。

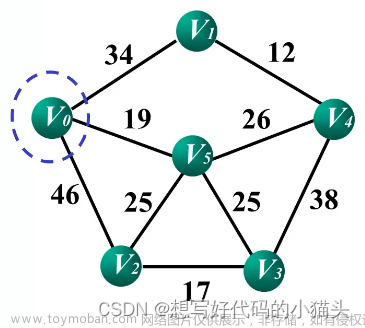
示例

编写程序用prim算法求解最小生成树,算法,算法,图论,数据结构
图的初始状态，将d数组全部设为无穷大。

编写程序用prim算法求解最小生成树,算法,算法,图论,数据结构

编写程序用prim算法求解最小生成树,算法,算法,图论,数据结构

每次找到集合T外距离集合T最近的点x，用x更新其他点到集合T的距离，当所有点不连通时，不存在最小生成树，即当更新过程中d[x] = inf，当所有的点都被加进集合T中，存在最小生成树。
上述示例最小生成树的树边权重之和为 4 + 8 + 1 + 2 + 4 + 2 + 7 + 9 = 37文章来源地址https://www.toymoban.com/news/detail-524549.html

三.代码示例

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510;
int g[N][N], dist[N];
int n, m;
bool st[N];

int prim()
{
    memset(dist, 0x3f, sizeof dist);
    
    int res = 0;
    for(int i = 0; i < n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
                
        st[t] = true;
        if(i && dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
        if(i) res += dist[t];
        
        for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    for(int i = 0; i < m; i++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        g[a][b] = g[b][a] = min(g[a][b], w);
    }
    
    int t = prim();
    if(t == 0x3f3f3f3f) puts("impossible");
    else printf("%d", t);
    return 0;
 }