目录
编辑距离:
举例:
代码如下
调试:
核心代码:
画图演示上述代码:
编辑距离:
是一种计算两个自符串之间差异程度的方法,它通过比较两个字符串之间的插入,删除和
替换操作的数量,来确定他们之间的距离。
举例:
现有两个字符串
字符串s1:”CTGA"
字符串s2: "ACGCTA"
求s1和s2的编辑距离
字符串s1得到字符串s2 可以通过如下操作
1. 在字符串s1的C前插入A ----------"ACTGA"
2. 在"ACTGA"字符串中,将T删除 ----------"ACGA"
3. 在"ACGA"字符G和A中插入C ----------"ACGCA"
4. 在"ACGCA"字符C和A中插入T----------"ACGCTA"
综上:字符串s1得到字符串s2至少花了4个步骤,因此字符串是s1与字符串s2之间的
编辑距离为4
代码如下
#include <stdio.h>
#define N 100
char A[N] = "CTGA";
char B[N] = "ACGCTA";
int d[N][N];
int min(int a, int b){
return a < b ? a : b;
}
int editdistance(char *str1, int len1, char *str2, int len2){
int i, j, temp;
for (i = 0; i <= len1; i++) {
d[i][0] = i;
}
for (j = 0; j <= len2; j++) {
d[0][j] = j;
}
for (i = 1; i <= len1; i++) {
for (j = 1; j <= len2; j++) {
if (str1[i - 1] == str2[j - 1]) {
d[i][j] = d[i - 1][j - 1];
} else {
temp = min(d[i - 1][j] + 1, d[i][j - 1] + 1);
d[i][j] = min(temp, d[i - 1][j - 1] + 1);
}
}
}
return d[len1][len2];
}
int main() {
int len1 = 4, len2 = 6;
printf("Edit distance between %s and %s is %d\n", A, B, editdistance(A, len1, B, len2));
system("pause");
return 0;
}调试:

通过运行,可知s1,s2的编辑距离4
核心代码:
for (i = 1; i <= len1; i++) {
for (j = 1; j <= len2; j++) {
if (str1[i - 1] == str2[j - 1]) {
d[i][j] = d[i - 1][j - 1];
} else {
temp = min(d[i - 1][j] + 1, d[i][j - 1] + 1);
d[i][j] = min(temp, d[i - 1][j - 1] + 1);
}
}
}
此段代码为该算法最核心部分
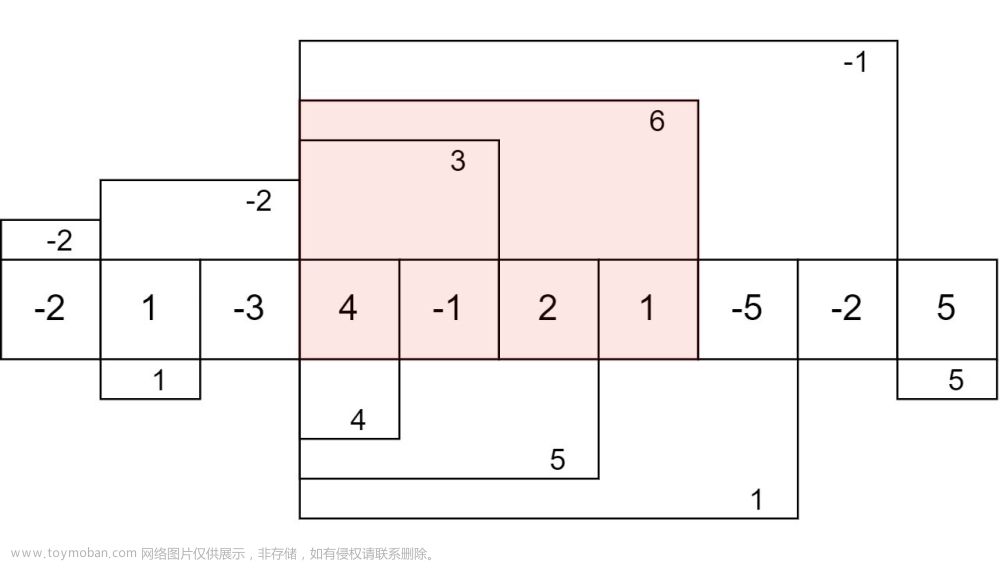
画图演示上述代码:
1.将d[0][0]更新为0,d[ i ][ 0 ]=i, d[ 0 ][ j ] =j

2.字符串s1的第一个字符是C,字符串s2的第1个字符是A,两者不相等
所以执行如下代码
else {
temp = min(d[i - 1][j] + 1, d[i][j - 1] + 1);
d[i][j] = min(temp, d[i - 1][j - 1] + 1);
}
i=1,j=1时
我们要在d[0][1] ,d[1][0],d[0][0],选出最小的值,并加1赋予d[i][j]

即选出图上三个数的最小的那个数,并且加1
得到
3.接下来看s1的第一个字符C,s2的第二个字符C,两者相等
此时数组的下标为d[1][2]
执行如下代码
if (str1[i - 1] == str2[j - 1]) {
d[i][j] = d[i - 1][j - 1];
}
将d[0][1]的值赋给d[1][2] 即d[1][2]的值为1

4.重复上面的操作
 文章来源:https://www.toymoban.com/news/detail-525109.html
文章来源:https://www.toymoban.com/news/detail-525109.html
d[ len1 ] [len2 ]的值为两个字符串的编辑距离文章来源地址https://www.toymoban.com/news/detail-525109.html
到了这里,关于【算法】动态规划算法求(编辑距离)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!