[github-100天机器学习]day3 multiple linear regression--代码版本问题已修正-Toy模板网

这篇具有很好参考价值的文章主要介绍了[github-100天机器学习]day3 multiple linear regression--代码版本问题已修正。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

https://github.com/LiuChuang0059/100days-ML-code/blob/master/Day3_Multiple_Linear_regression/README.md

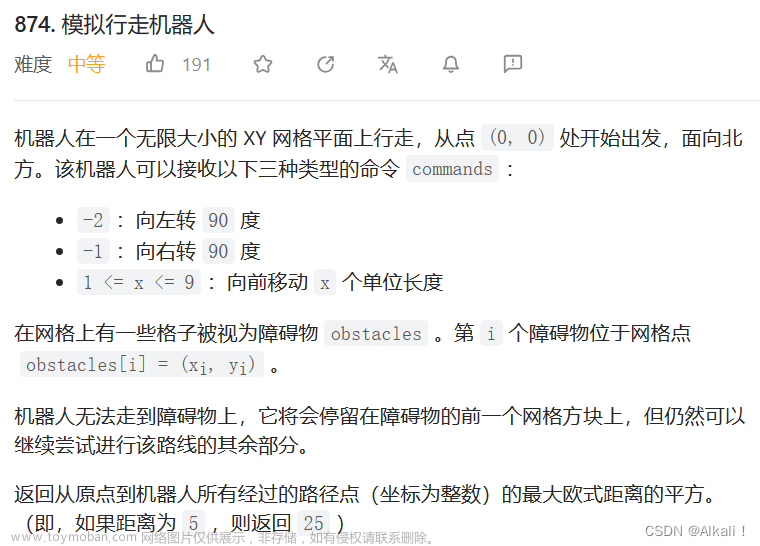
多元线性回归

一个线性方程适配观测数据，建立特征和响应之间的关系。可以用来找出预测结果在哪个因素影响最大，不同变量如何关联。

$y = b_0+b_1x_1+b_2x_2+...+b_nx_n$

前提：

线性：特征值和预测值线性相关
保持误差项的方差齐性(常数方差)：误差项的分散(方差)必须等同（线性回归的误差项在不同的预测值范围内有同样的方差，误差项的方差在各个预测值下保持不变。即误差项之间是独立的，一个误差不会影响其他误差。）—齐性
多元正态分布：多元回归假定残差符合正态分布(残差：实际观测值与模型估计值之间的差)
缺少多重共线性：假设数据有极少甚至没有多重特征。当特征不是相互独立的时候，会引发多重共线性。—独立性

ps： 误差（error）：是观察值与真实值之间的差，经典测量理论基本假设是–观察值等于真值加上误差。任何一次测量都带有误差（每一次测量的这个误差具体是多少是不清楚的，只有把所有测量结果进行分析后才知道误差有多大），经典测验理论认为误差是随机分布，且误差均值为0。因此，经过多次测验后，将观测值求平均就可以看作为真值。也就是说，多次测量求得的平均数是真值的最佳估计。**残差（residual）**是观察值与模型估计值之间的差。以回归分析为例，回归方程y=b0+b1x，当知道b0和b1时这就是一个真实的回归模型。比如y=2+3x。取一个数值（1,2），则模型估计值为y=2+3×1=5。残差为2-5=-3。因此，只要有一个确定的取值以及模型，则模型肯定有一个估计值，也就有一个残差了
来源：https://zhuanlan.zhihu.com/p/98643701
方差齐性，也就是方差相等。两组和多组比较中，方差齐性的意思很容易理解，无非就是比较各组的方差大小，看看各组的方差是不是差不多大小，如果差别太大，就认为是方差不齐，或方差不等。如果差别不大，就认为方差齐性或方差相等。这种所谓的差别大或小，需要统计学的检验，所以就有了方差齐性检验。
在线性回归中，有的人就不理解方差齐性是什么意思了。因为线性回归中自变量x不是分类变量，x取值很多。通常情况下，每个x值只对应1个y值。比如，分析身高对血压值的影响，可能每个身高对应的血压值只有一个数值。尽管在一次抽样中每个x取值上可能只有1个y值，但对于总体而言，理论上每个x取值上对应的y值是有很多的。尽管在一次抽样中每一身高值（如170cm）所对应的血压值可能只有1个值（如140mmHg），但从总体而言这一固定的身高（170cm）所对应的血压值应该有很多，可能是140mmHg，也可能是150mmHg，只是在我们的抽样中恰好抽中了这1个值而已。如果你重新抽样，170cm所对应的血压值可能就不是140mmHg了，有可能就是145mmHg或138mmHg等。所以，线性回归中，理论上也是有方差的。然而这种理论上的方差，除非你知道总体中每个x取值上的所有对应的y值，否则你是没有办法真正去计算方差的。但这种情况几乎是不可能发生的，因此在线性回归中的方差齐性检验，很多情况下只是一种探测而已。
来源：https://zhuanlan.zhihu.com/p/93270816

注意：

过多变量可能降低模型的精确度，尤其是对结果无关的变量，或存在对其他变量造成很大影响的变量。有一些变量选择方法：

向前选择法(forward selection): 一个个加入feature
(1)选择一个差异等级significance level，如SL=0.05表示有95%贡献
(2)建立回归模型，找到最小P值
(3)确立一个简单模型，将有最小P值的变量加入此模型
(4)如果P>SL，模型建立成功，否则转回(3)
向后选择法Backward Elimination：首先包含了所有的feature，然后每个feature都尝试去删除，测试删除的哪个feature对模型准确性有最大的提升，最终删掉对模型提升最高的一个特征。如此类推，直到删除feature并不能提升模型为止。
向前向后法：结合1和2，先用1筛选一遍，在用2筛选一遍，知道最后无论怎么筛选模型变量都不再发生变化。当一个feature新加入后，stepwise会尝试删去一个feature，直至达到某个预设的标准。这种方法的缺点是，预设的标准不好定，而且容易陷入到过拟合当中

虚(拟)变量

数据集是非数值数据类型时，使用分类数据时非常有效的。(分类数据：反映事物类别，是离散数据，分类属性有限且无序。如男女用0，1表示)

虚拟变量陷阱

虚拟变量限制指两个或两个以上变量之间高度相关，即存在一个能够被其他变量预测出的变量。（如一个存在重复类别的例子，舍弃男性类别，该类型也可用女性类别定义，即女性值为0表示男性）。

解决方法：变量类别减1：假定m个类别，模型构建取m-1个虚拟变量，减去的那个变量看作参照值。
$D_2 = 1- D_1$
$y = b_0+b_1x_1+b_2x_2+b_3D_1$

步骤：

数据预处理：导入库–导入数据集–检查缺失数据–数据分类–有必要则设置虚拟变量–特征缩放


## step1: 预处理

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[ : , :-1].values
Y = dataset.iloc[ : ,  4 ].values

from sklearn.compose import ColumnTransformer   #new
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[: , 3] = labelencoder.fit_transform(X[ : , 3])

ct = ColumnTransformer([('encoder', OneHotEncoder(), [0])], remainder='passthrough')#new
# 对第四列进行One-Hot编码转为二进制特征，[3]表示对第四列编码，转为数字标签
X = ct.fit_transform(X)#new

# onehotencoder = OneHotEncoder(categorical_features = [3]) #old
# X = onehotencoder.fit_transform(X).toarray()  #old

X = X[: , 1:]  #删除第一列
### 避免虚拟变量陷阱 只选择 两个（3-1）虚拟变量

from sklearn.model_selection import train_test_split    #new
#from sklearn.cross_validation import train_test_split   ## 分割数据集#old
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)

[github-100天机器学习]day3 multiple linear regression--代码版本问题已修正,ML100day,github,机器学习,线性回归

在训练集上训练模型：创建训练模型并用fit训练

## step2: 训练

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train) ## 多重线性回归模型应用到训练集

[github-100天机器学习]day3 multiple linear regression--代码版本问题已修正,ML100day,github,机器学习,线性回归

预测结果：在测试集预测predict()


## step3: 预测

y_pred = regressor.predict(X_test)

[github-100天机器学习]day3 multiple linear regression--代码版本问题已修正,ML100day,github,机器学习,线性回归

可视化


## step4:可视化
plt.scatter(np.arange(10),Y_test, color = 'red',label='y_test')
plt.scatter(np.arange(10),y_pred, color = 'blue',label='y_pred')
plt.legend(loc=2)
plt.show()