目录
一、总体和样本
二、集中趋势分析
2.1 均值
2.1.1 样本均值
2.1.2 总体均值
2.2 众数，中位数
三、离散趋势分析
3.1 总体方差
3.2 样本方差
3.3 标准差
一、总体和样本
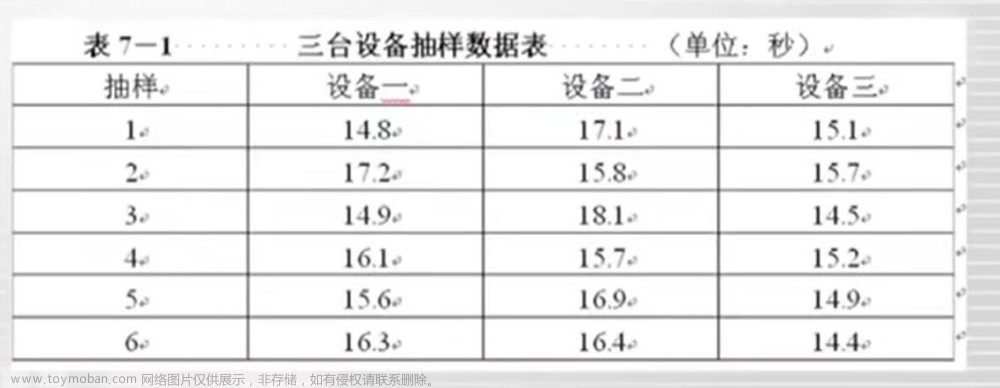
比如要计算全国男性的平均身高，但是全部调查是不现实的，所有要采取抽样调查，随机抽取一部分男性的身高，全国男性身高就是总体，被抽取的部分男性就是样本。
由于我们要计算全国男性的平均身高，所以就要计算均值，根据样本均值去推断总体均值，总体均值：μ，样本均值x拔，均值的计算方法都是一样的，用所有数据加起来的值/数据个数
二、集中趋势分析
2.1 均值
2.1.1 样本均值
：x拔=
（∑是求和，i=1的意思是从1开始，n的意思是一直加到n：X₁+X₂+……Xn）
2.1.2 总体均值
：μ=
2.2 众数，中位数
但是如果想知道数据离均值的远近程度，就要用到离散趋势分析
三、离散趋势分析
3.1 总体方差
例：
一组数据：2，2，3，3，总体均值为2.5
另一组数据：0，0，5，5，均值为2.5
但是第一组数据明显更集中于均值，而另一组相对分散，离均值较远
所以衡量方式就是方差
这个公式意义就是用每一个数据减去总体均值去计算差值（数据到均值的距离），平方的作用在于让差值为正，再除以数据个数 。
通过计算得出，第一组数据的方差时0.25，第二组数据的方差是6.25
3.2 样本方差
通常来说，当总体均值离样本均值距离比较小（值接近）时，可以用样本方差去估计总体方差，但是当数据的总体均值和样本均值差距较大，得到的结果就会有很大的偏差，就不能用样本均值去估计总体均值。
所以这时使用公式（这才是样本方差公式）（无偏样本方差）
文章来源：https://www.toymoban.com/news/detail-528799.html
3.3 标准差
标准差就是方差的平方根，为什么要使用标准差，因为标准差的单位更好，方差的单位是平方，而标准差的单位和数据的单位是一样的文章来源地址https://www.toymoban.com/news/detail-528799.html
到了这里，关于统计学学习笔记：L1-总体、样本、均值、方差的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
