为了在Python编程环境下实现卡尔曼滤波算法,特编写此程序
主要用到了以下3个模块
- numpy(数学计算)
- pandas(读取数据)
- matplotlib(画图展示)
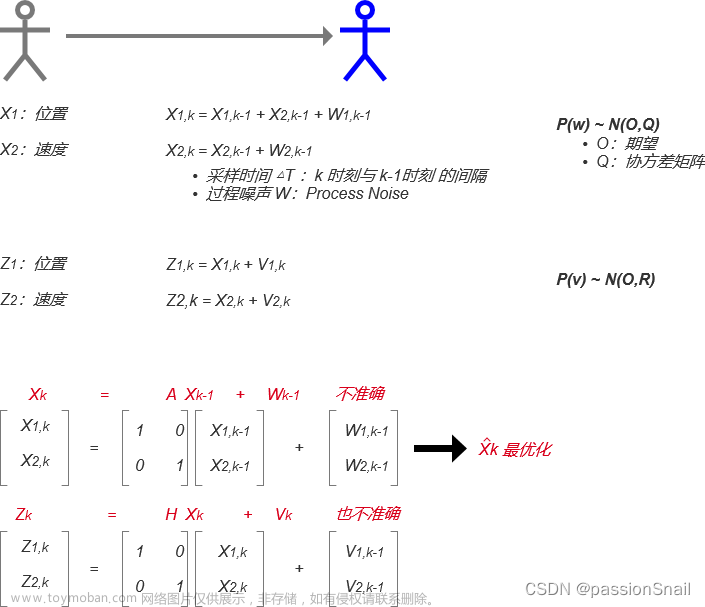
代码的核心是实现了一个Kf_Params类,该类定义了卡尔曼滤波算法的相关参数
然后是实现了一个kf_init()函数,用来初始化卡尔曼滤波算法的相关参数
接着实现了一个kf_update()函数,用来更新卡尔曼滤波算法的相关参数
最后在主程序中读取数据,并调用卡尔曼滤波算法预测数据
数据样例见评论区的网盘链接,完整代码如下:
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
font = {'family': 'SimSun', # 宋体
# 'weight': 'bold', # 加粗
'size': '10.5' # 五号
}
plt.rc('font', **font)
plt.rc('axes', unicode_minus=False)
# plt.rcParams['figure.facecolor'] = "#FFFFF0" # 设置窗体颜色
# plt.rcParams['axes.facecolor'] = "#FFFFF0" # 设置绘图区颜色
class Kf_Params:
B = 0 # 外部输入为0
u = 0 # 外部输入为0
K = float('nan') # 卡尔曼增益无需初始化
z = float('nan') # 这里无需初始化,每次使用kf_update之前需要输入观察值z
P = np.diag(np.ones(4)) # 初始P设为0 ??? zeros(4, 4)
# 初始状态:函数外部提供初始化的状态,本例使用观察值进行初始化,vx,vy初始为0
x = []
G = []
# 状态转移矩阵A
# 和线性系统的预测机制有关,这里的线性系统是上一刻的位置加上速度等于当前时刻的位置,而速度本身保持不变
A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
# 预测噪声协方差矩阵Q:假设预测过程上叠加一个高斯噪声,协方差矩阵为Q
# 大小取决于对预测过程的信任程度。比如,假设认为运动目标在y轴上的速度可能不匀速,那么可以把这个对角矩阵
# 的最后一个值调大。有时希望出来的轨迹更平滑,可以把这个调更小
Q = np.diag(np.ones(4)) * 0.1
# 观测矩阵H:z = H * x
# 这里的状态是(坐标x, 坐标y, 速度x, 速度y),观察值是(坐标x, 坐标y),所以H = eye(2, 4)
H = np.eye(2, 4)
# 观测噪声协方差矩阵R:假设观测过程上存在一个高斯噪声,协方差矩阵为R
# 大小取决于对观察过程的信任程度。比如,假设观测结果中的坐标x值常常很准确,那么矩阵R的第一个值应该比较小
R = np.diag(np.ones(2)) * 0.1
def kf_init(px, py, vx, vy):
# 本例中,状态x为(坐标x, 坐标y, 速度x, 速度y),观测值z为(坐标x, 坐标y)
kf_params = Kf_Params()
kf_params.B = 0
kf_params.u = 0
kf_params.K = float('nan')
kf_params.z = float('nan')
kf_params.P = np.diag(np.ones(4))
kf_params.x = [px, py, vx, vy]
kf_params.G = [px, py, vx, vy]
kf_params.A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
kf_params.Q = np.diag(np.ones(4)) * 0.1
kf_params.H = np.eye(2, 4)
kf_params.R = np.diag(np.ones(2)) * 0.1
return kf_params
def kf_update(kf_params):
# 以下为卡尔曼滤波的五个方程(步骤)
a1 = np.dot(kf_params.A, kf_params.x)
a2 = kf_params.B * kf_params.u
x_ = np.array(a1) + np.array(a2)
b1 = np.dot(kf_params.A, kf_params.P)
b2 = np.dot(b1, np.transpose(kf_params.A))
p_ = np.array(b2) + np.array(kf_params.Q)
c1 = np.dot(p_, np.transpose(kf_params.H))
c2 = np.dot(kf_params.H, p_)
c3 = np.dot(c2, np.transpose(kf_params.H))
c4 = np.array(c3) + np.array(kf_params.R)
c5 = np.linalg.matrix_power(c4, -1)
kf_params.K = np.dot(c1, c5)
d1 = np.dot(kf_params.H, x_)
d2 = np.array(kf_params.z) - np.array(d1)
d3 = np.dot(kf_params.K, d2)
kf_params.x = np.array(x_) + np.array(d3)
e1 = np.dot(kf_params.K, kf_params.H)
e2 = np.dot(e1, p_)
kf_params.P = np.array(p_) - np.array(e2)
kf_params.G = x_
return kf_params
def accuracy(predictions, labels):
return np.array(predictions) - np.array(labels)
if __name__ == '__main__':
# 真实路径
path = './9.xlsx'
data_A = pd.read_excel(path, header=None)
data_A_x = list(data_A.iloc[::, 0])
data_A_y = list(data_A.iloc[::, 1])
A = np.array(list(zip(data_A_x, data_A_y)))
# plt.subplot(131)
plt.figure()
plt.plot(data_A_x, data_A_y, 'b-+')
# plt.title('实际的真实路径')
# 检测到的路径
path = './10.xlsx'
data_B = pd.read_excel(path, header=None)
data_B_x = list(data_B.iloc[::, 0])
data_B_y = list(data_B.iloc[::, 1])
B = np.array(list(zip(data_B_x, data_B_y)))
# plt.subplot(132)
plt.plot(data_B_x, data_B_y, 'r-+')
# plt.title('检测到的路径')
# 卡尔曼滤波
kf_params_record = np.zeros((len(data_B), 4))
kf_params_p = np.zeros((len(data_B), 4))
t = len(data_B)
kalman_filter_params = kf_init(data_B_x[0], data_B_y[0], 0, 0)
for i in range(t):
if i == 0:
kalman_filter_params = kf_init(data_B_x[i], data_B_y[i], 0, 0) # 初始化
else:
# print([data_B_x[i], data_B_y[i]])
kalman_filter_params.z = np.transpose([data_B_x[i], data_B_y[i]]) # 设置当前时刻的观测位置
kalman_filter_params = kf_update(kalman_filter_params) # 卡尔曼滤波
kf_params_record[i, ::] = np.transpose(kalman_filter_params.x)
kf_params_p[i, ::] = np.transpose(kalman_filter_params.G)
kf_trace = kf_params_record[::, :2]
kf_trace_1 = kf_params_p[::, :2]
# plt.subplot(133)
plt.plot(kf_trace[::, 0], kf_trace[::, 1], 'g-+')
plt.plot(kf_trace_1[1:26, 0], kf_trace_1[1:26, 1], 'm-+')
legend = ['CMA最佳路径数据集', '检测路径', '卡尔曼滤波结果', '预测路径']
plt.legend(legend, loc="best", frameon=False)
plt.title('卡尔曼滤波后的效果')
plt.savefig('result.svg', dpi=600)
plt.show()
# plt.close()
p = accuracy(kf_trace, A)
print(p)
卡尔曼滤波处理结果如下:

可以看到,通过卡尔曼滤波算法预测的数据与真实的数据相差不大,成功实现了该算法
更新:2022年11月19日
更新说明:
- 将三个init、update、accuracy三个函数放在对象KalmanFilter内
- 修改了一些有意义的变量名,方便理解卡尔曼滤波器工作过程
- 丰富了滤波器输出数据的精度评价表格
- 修改了一些注释
- 增加了一个导弹跟踪敌机的卡尔曼滤波实例
代码如下:
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
font = {'family': 'SimSun', # 宋体
'weight': 'bold', # 加粗
'size': '10.5' # 五号
}
plt.rc('font', **font)
plt.rc('axes', unicode_minus=False)
plt.rcParams['figure.facecolor'] = "#FFFFF0" # 设置窗体颜色
plt.rcParams['axes.facecolor'] = "#FFFFF0" # 设置绘图区颜色
class KalmanFilter:
B = 0 # 控制变量矩阵,初始化为0
u = 0 # 状态控制向量,初始化为0
K = float('nan') # 卡尔曼增益无需初始化
z = float('nan') # 观测值无需初始化,由外界输入
P = np.diag(np.ones(4)) # 先验估计协方差
x = [] # 滤波器输出状态
G = [] # 滤波器预测状态
# 状态转移矩阵A,和线性系统的预测机制有关
A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
# 噪声协方差矩阵Q,代表对控制系统的信任程度,预测过程上叠加一个高斯噪声,若希望跟踪的轨迹更平滑,可以调小
Q = np.diag(np.ones(4)) * 0.1
# 观测矩阵H:z = H * x,这里的状态是(坐标x, 坐标y, 速度x, 速度y),观察值是(坐标x, 坐标y)
H = np.eye(2, 4)
# 观测噪声协方差矩阵R,代表对观测数据的信任程度,观测过程上存在一个高斯噪声,若观测结果中的值很准确,可以调小
R = np.diag(np.ones(2)) * 0.1
def init(self, px, py, vx, vy):
# 本例中,状态x为(坐标x, 坐标y, 速度x, 速度y),观测值z为(坐标x, 坐标y)
self.B = 0
self.u = 0
self.K = float('nan')
self.z = float('nan')
self.P = np.diag(np.ones(4))
self.x = [px, py, vx, vy]
self.G = [px, py, vx, vy]
self.A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
self.Q = np.diag(np.ones(4)) * 0.1
self.H = np.eye(2, 4)
self.R = np.diag(np.ones(2)) * 0.1
def update(self):
# Xk_ = Ak*Xk-1+Bk*Uk
a1 = np.dot(self.A, self.x)
a2 = self.B * self.u
x_ = np.array(a1) + np.array(a2)
self.G = x_
# Pk_ = Ak*Pk-1*Ak'+Q
b1 = np.dot(self.A, self.P)
b2 = np.dot(b1, np.transpose(self.A))
p_ = np.array(b2) + np.array(self.Q)
# Kk = Pk_*Hk'/(Hk*Pk_*Hk'+R)
c1 = np.dot(p_, np.transpose(self.H))
c2 = np.dot(self.H, p_)
c3 = np.dot(c2, np.transpose(self.H))
c4 = np.array(c3) + np.array(self.R)
c5 = np.linalg.matrix_power(c4, -1)
self.K = np.dot(c1, c5)
# Xk = Xk_+Kk(Zk-Hk*Xk_)
d1 = np.dot(self.H, x_)
d2 = np.array(self.z) - np.array(d1)
d3 = np.dot(self.K, d2)
self.x = np.array(x_) + np.array(d3)
# Pk = Pk_-Kk*Hk*Pk_
e1 = np.dot(self.K, self.H)
e2 = np.dot(e1, p_)
self.P = np.array(p_) - np.array(e2)
def accuracy(self, predictions, labels):
return np.array(predictions) / np.array(labels)
if __name__ == '__main__':
# 读取真实路径数据(客观真实的数据,作为滤波器预测结果的对比标签)
# 比如敌机的真实飞行轨迹
path = './9.xlsx'
label = pd.read_excel(path, header=None)
label_x = list(label.iloc[::, 0])
label_y = list(label.iloc[::, 1])
label_data = np.array(list(zip(label_x, label_y)))
# 读取检测路径数据(传感器检测到的原始数据,与真实值之间会存在误差,作为滤波器的输入)
# 比如我方导弹获取的敌机飞行轨迹,只能获取到当前时刻之前的轨迹信息,而不能直接获取未来的轨迹
path = './10.xlsx'
detect = pd.read_excel(path, header=None)
detect_x = list(detect.iloc[::, 0])
detect_y = list(detect.iloc[::, 1])
detect_data = np.array(list(zip(detect_x, detect_y)))
# 可视化(对原始数据进行可视化)
plt.figure()
plt.plot(label_x, label_y, 'b-+')
plt.plot(detect_x, detect_y, 'r-+')
# 卡尔曼滤波(根据卡尔曼对当前时刻的预测数据和当前时刻的观测数据,尽可能地输出下一时刻接近真实数据的数据)
# 实现对敌机未来飞行轨迹的估计,达到跟踪目标的效果
t = len(detect_data) # 处理时刻
kf_data_filter = np.zeros((t, 4)) # 滤波数据
kf_data_predict = np.zeros((t, 4)) # 预测数据
# 初始化(创建滤波器,并初始化滤波器状态)
kf = KalmanFilter()
kf.init(detect_x[0], detect_y[0], 0, 0)
# 滤波处理(依次读取每一时刻的数据,输入到卡尔曼滤波器,输出预测结果)
for i in range(t):
if i == 0:
kf.init(detect_x[i], detect_y[i], 0, 0) # 初始化
else:
kf.z = np.transpose([detect_x[i], detect_y[i]]) # 获取当前时刻的观测数据
kf.update() # 更新卡尔曼滤波器参数
kf_data_filter[i, ::] = np.transpose(kf.x)
kf_data_predict[i, ::] = np.transpose(kf.G)
kf_filter = kf_data_filter[::, :2]
kf_predict = kf_data_predict[::, :2]
# 评价(计算卡尔曼滤波器的预测精度)
precision_detect = kf.accuracy(detect_data, label_data)
precision_filter = kf.accuracy(kf_filter, label_data)
print("-"*100)
print("%-4s \t %-20s \t %-20s \t %-20s \t %-20s " % (
"time", "detect gap x", "filter gap x", "detect gap y", "filter gap y"))
print("-"*100)
for i in range(len(precision_filter)):
print("%-4s \t %-20s \t %-20s \t %-20s \t %-20s " % (i,
precision_detect[i][0], precision_filter[i][0],
precision_detect[i][1], precision_filter[i][1]))
print("-"*100)
# 可视化(对滤波结果进行可视化)
plt.plot(kf_filter[::, 0], kf_filter[::, 1], 'g-+')
plt.plot(kf_predict[::, 0], kf_predict[::, 1], 'm-+')
legend = ['reality data', 'detect data', 'filter data', 'predict data']
plt.legend(legend, loc="best", frameon=False)
plt.title('kalman filter')
plt.savefig('result.svg', dpi=600)
plt.show()
运行后输出数据如下:

最后给出一个发射导弹跟踪敌机的应用实例如下:
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import matplotlib.animation as animation
import sympy
import random
# 卡尔曼滤波器
class KalmanFilter:
B = 0 # 控制变量矩阵,初始化为0
u = 0 # 状态控制向量,初始化为0
K = float('nan') # 卡尔曼增益无需初始化
z = float('nan') # 观测值无需初始化,由外界输入
P = np.diag(np.ones(4)) # 先验估计协方差
x = [] # 滤波器输出状态
G = [] # 滤波器预测状态
# 状态转移矩阵A,和线性系统的预测机制有关
A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
# 噪声协方差矩阵Q,代表对控制系统的信任程度,预测过程上叠加一个高斯噪声,若希望跟踪的轨迹更平滑,可以调小
Q = np.diag(np.ones(4)) * 0.1
# 观测矩阵H:z = H * x,这里的状态是(坐标x, 坐标y, 速度x, 速度y),观察值是(坐标x, 坐标y)
H = np.eye(2, 4)
# 观测噪声协方差矩阵R,代表对观测数据的信任程度,观测过程上存在一个高斯噪声,若观测结果中的值很准确,可以调小
R = np.diag(np.ones(2)) * 0.1
def init(self, px, py, vx, vy):
# 本例中,状态x为(坐标x, 坐标y, 速度x, 速度y),观测值z为(坐标x, 坐标y)
self.B = 0
self.u = 0
self.K = float('nan')
self.z = float('nan')
self.P = np.diag(np.ones(4))
self.x = [px, py, vx, vy]
self.G = [px, py, vx, vy]
self.A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
self.Q = np.diag(np.ones(4)) * 0.1
self.H = np.eye(2, 4)
self.R = np.diag(np.ones(2)) * 0.1
def update(self):
# Xk_ = Ak*Xk-1+Bk*Uk
a1 = np.dot(self.A, self.x)
a2 = self.B * self.u
x_ = np.array(a1) + np.array(a2)
self.G = x_
# Pk_ = Ak*Pk-1*Ak'+Q
b1 = np.dot(self.A, self.P)
b2 = np.dot(b1, np.transpose(self.A))
p_ = np.array(b2) + np.array(self.Q)
# Kk = Pk_*Hk'/(Hk*Pk_*Hk'+R)
c1 = np.dot(p_, np.transpose(self.H))
c2 = np.dot(self.H, p_)
c3 = np.dot(c2, np.transpose(self.H))
c4 = np.array(c3) + np.array(self.R)
c5 = np.linalg.matrix_power(c4, -1)
self.K = np.dot(c1, c5)
# Xk = Xk_+Kk(Zk-Hk*Xk_)
d1 = np.dot(self.H, x_)
d2 = np.array(self.z) - np.array(d1)
d3 = np.dot(self.K, d2)
self.x = np.array(x_) + np.array(d3)
# Pk = Pk_-Kk*Hk*Pk_
e1 = np.dot(self.K, self.H)
e2 = np.dot(e1, p_)
self.P = np.array(p_) - np.array(e2)
def accuracy(self, predictions, labels):
return np.array(predictions) / np.array(labels)
# 读取敌机飞行数据
path = './9.xlsx'
label = pd.read_excel(path, header=None)
label_x = list(label.iloc[::, 0])
label_y = list(label.iloc[::, 1])
label_data = np.array(list(zip(label_x, label_y)))
# 读取我方雷达对敌机的侦查数据
path = './10.xlsx'
detect = pd.read_excel(path, header=None)
detect_x = list(detect.iloc[::, 0])
detect_y = list(detect.iloc[::, 1])
detect_data = np.array(list(zip(detect_x, detect_y)))
# 创建卡尔曼滤波器
t = len(detect_data) # 处理时刻
kf_data_filter = np.zeros((t, 4)) # 滤波数据
kf_data_predict = np.zeros((t, 4)) # 预测数据
kf = KalmanFilter() # 创建滤波器
kf.init(detect_x[0], detect_y[0], 0, 0) # 滤波器初始化
# 生成地图画布
fig, ax = plt.subplots(1, 1)
plt.grid(ls='--')
ax.set_xlim(600, 800)
ax.set_ylim(300, 700)
# 初始化信息
fly_data_x = [label_data[0][0], ]
fly_data_y = [label_data[0][1], ]
missile_data_x = [625, ]
missile_data_y = [350, ]
line_fly, = plt.plot(fly_data_x[0],fly_data_y[0], 'r-')
line_missile, = plt.plot(missile_data_x[0], missile_data_y[0], 'g-')
hit_flag = 0
hit_frame = -1
trace_flag = 1
# 计算我方导弹下一次的移动坐标
def missile_move(loc):
global hit_flag
solve_x = 0
solve_y = 0
x1, y1, x2, y2 = loc
dist = ((x1-x2)**2 + (y1-y2)**2)**(1/2)
max_dist = max(0.08*dist, 10)
move_dist = min(max_dist*(0.6+random.random()), max_dist)
if abs(dist - move_dist) < 5:
hit_flag = 1
x, y = sympy.symbols("x y")
res = sympy.solve(
[(y2-y1)*(x-x1) - (y-y1)*(x2-x1),
((x-x1)**2 + (y-y1)**2)**(1/2) - move_dist],
[x, y]
)
for i in range(len(res)):
if res[i][0] > min(x1, x2) and res[i][0] < max(x1, x2):
solve_x =res[i][0]
solve_y =res[i][1]
break
else:
solve_x = x1
solve_y = y1
return solve_x, solve_y
# 初始化敌机、我方导弹位置
def fly_init():
line_fly.set_data(fly_data_x, fly_data_y)
line_missile.set_data(missile_data_x, missile_data_y)
return line_fly, line_missile,
# 刷新敌机、我方导弹实时运动轨迹
def fly_update(frames):
global fly_data_x, fly_data_y, missile_data_x, missile_data_y
global line_fly, line_missile
global hit_flag, hit_frame, trace_flag
if hit_flag:
hit_flag = 0
trace_flag = 0
hit_frame = frames.copy()
plt.cla()
plt.grid(ls='--')
ax.set_xlim(600, 800)
ax.set_ylim(300, 700)
line_fly, = plt.plot(label_data[frames-1][0], label_data[frames-1][1], 'b*')
line_missile, = plt.plot(label_data[frames-1][0], label_data[frames-1][1], 'b*')
if hit_frame >= 0 and (frames >= hit_frame + 1):
hit_frame = -1
trace_flag = 0
if frames >= (len(label_data) - 1):
trace_flag = 1
fly_data_x = [label_data[0][0], ]
fly_data_y = [label_data[0][1], ]
missile_data_x = [625, ]
missile_data_y = [350, ]
plt.cla()
plt.grid(ls='--')
ax.set_xlim(600, 800)
ax.set_ylim(300, 700)
line_fly, = plt.plot(fly_data_x[0],fly_data_y[0], 'r-')
line_missile, = plt.plot(missile_data_x[0], missile_data_y[0], 'g-')
else:
if trace_flag:
fly_data_x.append(label_data[frames][0])
fly_data_y.append(label_data[frames][1])
line_fly.set_data(fly_data_x, fly_data_y)
# ------关键处理步骤------
kf.z = np.transpose([detect_x[frames], detect_y[frames]]) # 获取最新的观测数据
kf.update() # 更新卡尔曼滤波器参数
kf_data_filter[frames, ::] = np.transpose(kf.x) # 滤波器输出
loc = missile_data_x[frames-1], missile_data_y[frames-1],\
kf_data_filter[frames][0], kf_data_filter[frames][1]
# ------关键处理步骤------
move_x, move_y = missile_move(loc)
missile_data_x.append(move_x)
missile_data_y.append(move_y)
line_missile.set_data(missile_data_x, missile_data_y)
return line_fly, line_missile,
fly_anim = animation.FuncAnimation(fig=fig, func=fly_update,
frames=np.arange(1, len(label_data)),
init_func=fly_init, interval=100, blit=True)
plt.title('kalman filter trace object')
legend = ['fly', 'missile']
plt.legend(legend, loc="best", frameon=False)
fly_anim.save('animation.gif', writer='pillow', fps=10)
plt.show()
动画展示跟踪效果如下:

上文仅仅是为了更好的理解卡尔曼滤波器,自己实现了相关的核心代码
若有更高的要求,filterpy模块中给出了更权威的卡尔曼滤波器,可以直接导入使用
from filterpy.kalman import KalmanFilter卡尔曼滤波已经是一种最基本的滤波算法,结合其它算法,可以在广阔的场景下实现更强大的功能
比如作者曾经使用过的sort、deepsort等算法,其核心就是卡尔曼滤波算法文章来源:https://www.toymoban.com/news/detail-528979.html
探索未知并能成功应用到预期的场景是一件有趣的事情,祝愿大家能在科研、工作上取得更多成果文章来源地址https://www.toymoban.com/news/detail-528979.html
到了这里,关于卡尔曼滤波的Python实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!